ボーアの水素原子模型とは?【写経して原子分野を突破せよ】

どうも!オンライン物理塾長あっきーです!現役で早稲田大学に合格し、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
今回は「ボーアの水素原子模型」を扱っていきます。
ボーアの水素原子模型は入試にもよく問われる問題です。
「原子分野なんかやらなくていいや~」なんて思っていて、ボーアの水素原子模型が出てたら詰みます。
だからやっておいた方が良いです。
ボーアの水素原子模型の解法はたった1つです。
写経です。
詳しく見ていきましょう!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
ボーアの原子模型の流れを写経せよ!
目次
ボーアの原子模型とは?
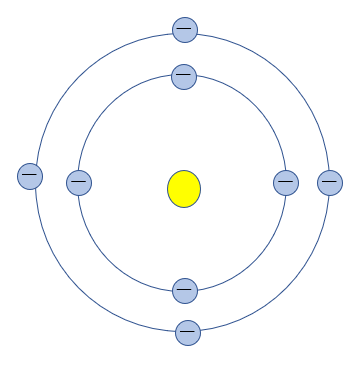
ボーアの原子模型とはボーアという人が考案した原子の形です。
高校生のみなさんなら「原子核の周りを電子が周る」という原子の形を知っていますよね。あれをボーアさんが考えたわけです。
ラザフォードの原子模型の問題を解決した
実は、「原子核の周りを電子が周る」という考え方はラザフォードが最初に考えていました。
しかしこの形には一つ問題があって、電子は運動すると電磁波を放射します。
それによってエネルギーが小さくなり、次第に原子核にぶつかってしまうのです。
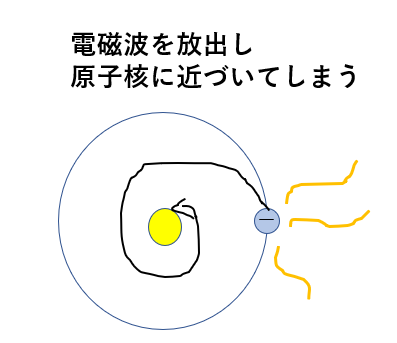
そこで、新しく考えだされたものがボーアの原子模型ということなのです。
ボーアの原子模型は写経せよ
では、ボーアの原子模型について詳しく見ていきますが、今から書く内容は写経して覚えてください。
これがボーアの原子模型の解法です。
入試ではボーアの原子模型で問われることは決まっていて、原子模型の流れを理解するだけですべて解けます。
なので、写経してください。
ボーアの水素原子模型1:ボーアの量子条件
ボーアは電子が決まった半径の円運動のみできると考えました。
電子の波(物質波)の波長が整数倍である半径のみを取り、その半径で円運動する電子は電磁波を放射しないと考えたのです。
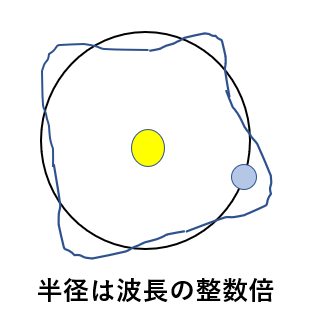
半径\(r\), 波長\(\lambda\)として、整数\(n\)を用いると次の関係が成り立ちます。
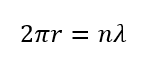
物質波には次のような関係があります。
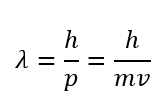
\(h\)はプランク定数、\(p\)は運動量です。
これを用いて式を書き直しましょう。
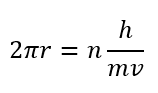
この条件を量子条件と言います。
\(n\)を量子数と言い、この条件を満たす電子の状態を定常状態と言います。
定常状態における電子のエネルギーは電磁波を放出しないので、固有のエネルギーを持つことができ、このエネルギーをエネルギー準位と呼びます。
ボーアの水素原子模型2:ボーアの振動数条件
次にエネルギーの関係を見ていきます。
電子は半径に応じたエネルギー準位を持っています。
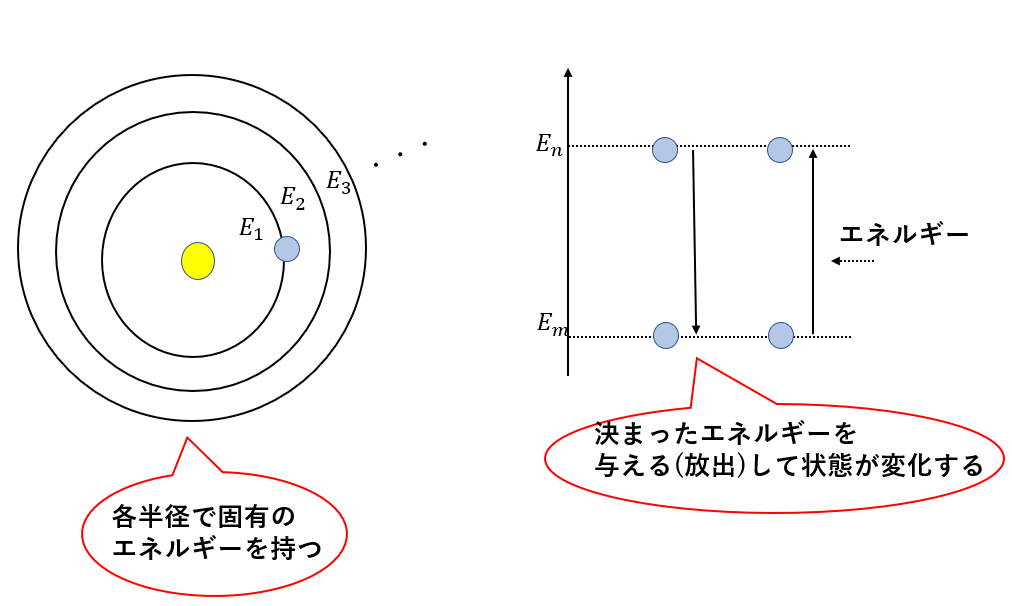
なので、半径を変えるには決まったエネルギーを与える必要があります。
この与えるエネルギーは光子のエネルギーに一致します。
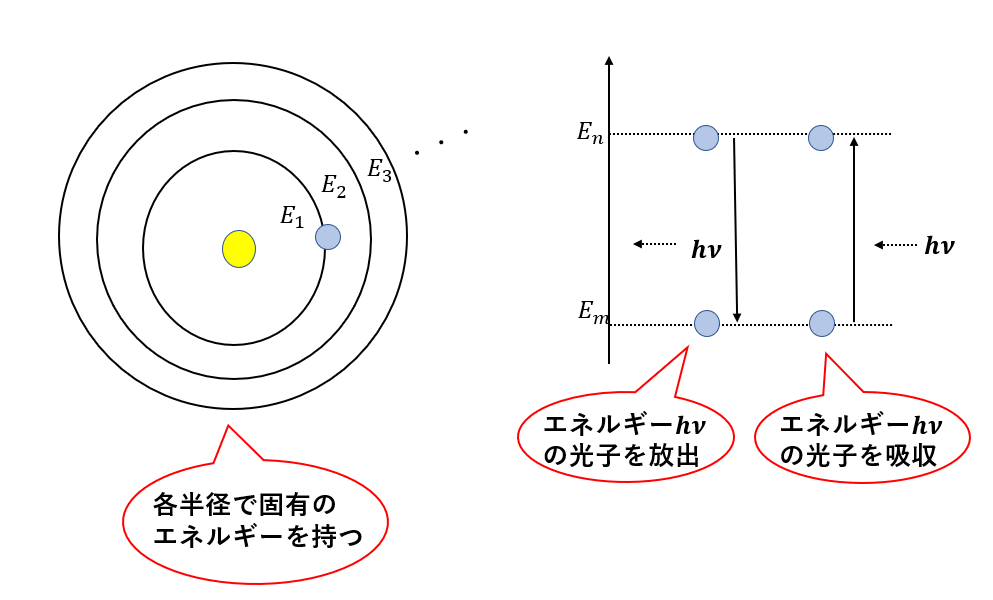
エネルギー準位\(E_{m}\)から\(E_n\)に移るとき、以下の関係が成り立ちます。
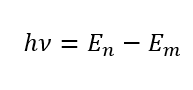
これをボーアの振動数条件と呼びます。
2つの条件はボーアの原子模型を考えるための仮定だと思ってください。ここから原子模型について見ていきます。
ボーアの原子模型3:電子の軌道半径を求める
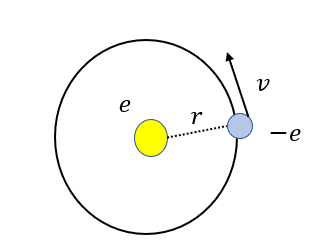
質量\(m\),電荷量\(-e\)の電子が速さ\(v\)で等速円運動している場合を考えます(原子なので原子核の電気量は\(+e\)です)。
この電子について運動方程式を立てます。
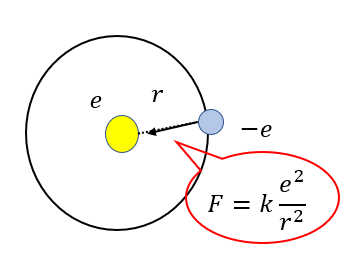
電子には静電気力がはたらいています。その大きさは\(F = k\frac{e^2}{r^2}\)で、中心向きにはたらいていますね。
この力によって円運動しているので運動方程式は以下のように立てられます。
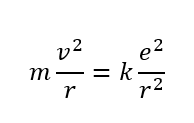
これと先ほどのボーアの量子条件を使って\(v\)を消去することで半径\(r\)が求められます。
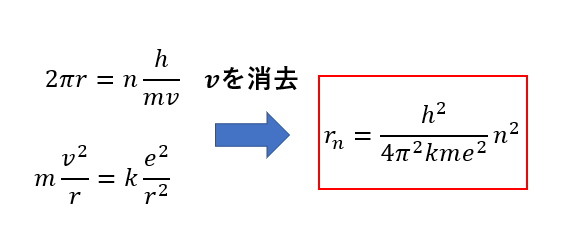
(\(n\)によって変化するので\(r_n\)と表記しています。)
\(n=1,2…\)と飛び飛びの値を取るため、\(r_n\)の値も飛び飛びの値をとります。
これがまさに\(K\)殻、\(L\)殻・・・となることを表しています。
特に\(n=1\)のときの半径をボーア半径と呼んだりします。
ボーアの原子模型4:エネルギー準位
次にエネルギー準位を求めていきます。
電子は運動エネルギーと静電気力による位置エネルギーを持っています。
これらの和を取ることでエネルギー準位を導けますね。
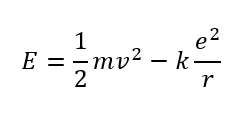
これに運動方程式と先ほど求めた\(r\)を代入するとエネルギー準位を求めることができます。
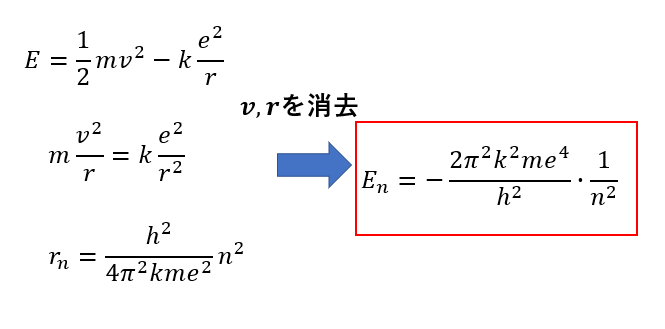
(これも\(n\)によって決まるので、\(E\)を\(E_n\)と書き換えています)
\(n=1\)のときが最もエネルギーが低く安定な状態となり、\(n\)が大きくなるにつれてエネルギーが大きくなります。
\(n=1\)のときの状態を基底状態、それ以外を励起状態と呼びます。
ボーアの原子模型5:水素原子スペクトル
最後に波長(水素原子のスペクトル)について考えます。
先ほど求めたエネルギー準位とボーアの振動数条件から波長\(\lambda\)が求められます。
ここで\(c = \nu \lambda\)を使うことに注意しましょう。
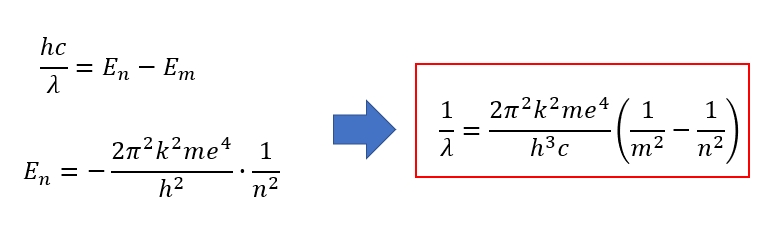
これにより水素原子の波長(スペクトル)を特定するとことができます。
このうち以下の部分をリュードベリ定数と呼ばれています。
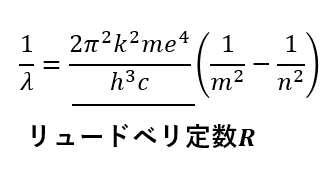
これにてボーアの原子模型は終了です。
まとめ:ボーアの原子模型は写経せよ
いかがでしたか?
ボーアの原子模型は今やった流れを写経してください。
最後に大まかな流れをまとめておくので、これを踏まえてボーアの原子模型の流れを完コピしてください。
ボーアの原子模型も流れ
- ボーアの量子条件
- ボーアの振動条件
- 電子軌道の半径を求める
- エネルギー準位を求める
- 波長(の逆数)を求める