コンプトン効果=運動量とエネルギー問題
どうも。今回は原子分野の「コンプトン効果」っていうのをやっていこう!
コンプトン効果はただの運動量とエネルギーの問題なので、力学をしっかり学んだ人には楽勝なところだと思います。
コンプトン効果はほとんど流れが決まっているので、一度その流れをつかんじゃってもOK。
| まずはチェック! エネルギー→仕事とエネルギー ~エネルギー原理で受験突破~ 運動量→運動量 |
コンプトン効果って何?
コンプトン効果っていうのは、超簡単に言えば・・・
光電効果では、光のエネルギーによって電子を飛び出せることができる。(光電効果についてはこちら)
光電効果では電子のみを考えたから、エネルギーを与えた後の光については触れていなかったんだけど、
コンプトン効果では主役を光にしようっていうことです。
光子のエネルギーってのは
\( E = \frac{hc}{\lambda}\)
で表せたよね。んで、エネルギーを電子に与えたってことはこのエネルギーは減りそうだよね。ってことは・・・
「波長が長くなるんじゃね?」
ってことで、それを導いてみよう!!
ただ、コンプトン効果っていうのはX線レベルの非常に短い波長の波で起こるので、ここではX線が登場します。が、扱い方は光と全く同じです。
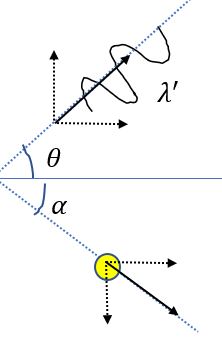
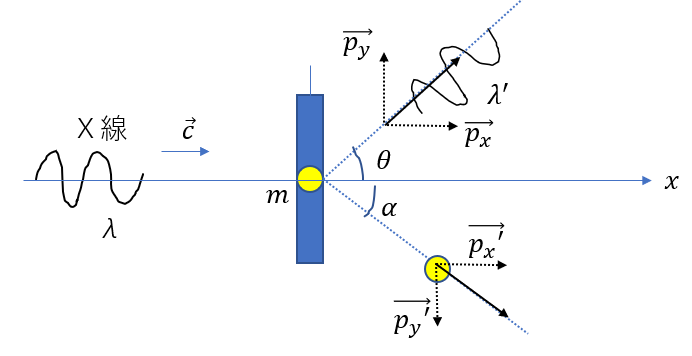
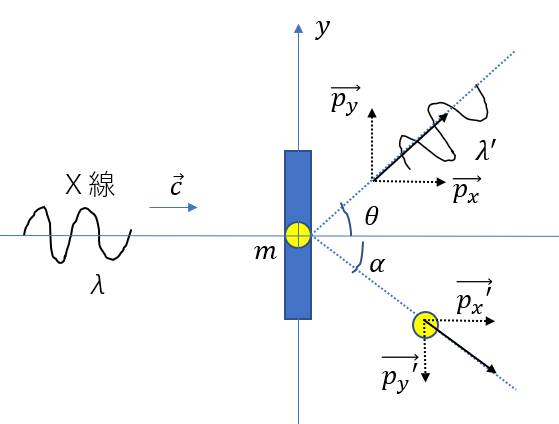
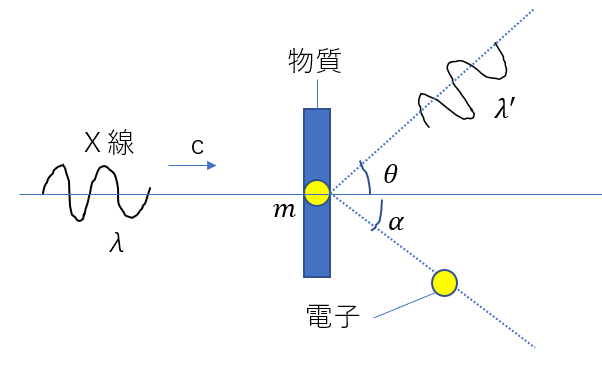
| (問) 波長\(\lambda\)のX線を物質に入射する。X線を粒子からできる物質とすれば、電子との衝突を考えることができる。衝突によって、電子とX線はそれぞれ図のように\(\alpha, \theta\)の向きに動く。衝突後のX線の波長を\(\lambda’\)としたときに、波長差\(\Delta \lambda = \lambda ‘ – \lambda \)を求めよ。ただし、電子の質量をm、光速をc、プランク定数をhとし、衝突は弾性衝突であるとする。 |
光子と電子のエネルギー保存
まず、エネルギー保存を考えてみよう。
(はじめのエネルギー)+(された仕事)=(あとのエネルギー)
なので、X線がされた仕事をWとして、
X線 : \(\frac{hc}{\lambda} + W = \frac{hc}{\lambda’}\)
電子: \(0 + (-W) = \frac{1}{2}mv^2\)
X線がWの仕事をされれば電子は-Wの仕事をされるのはわかるよね。
これらを足してあげれば・・・
\(\frac{hc}{\lambda} = \frac{hc}{\lambda’} + \frac{1}{2}mv^2\)・・・①
X線と電子の運動量保存
次に運動量を考えましょう。
衝突後は、斜めのになってしまっているので、まず水平と垂直に分けましょう。
今回、光子の運動量っていうのを扱うのですが、光子の運動量はこう定義されます。
\(p = \frac{E}{c} = \frac{h}{\lambda}\)
運動量ってベクトルなので、しっかり向きを考えます。
運動量を扱うので当然ベクトルです。なので、軸を取りましょう。
水平と垂直を別々で考えるのでまずは、水平からいこう。
水平方向の運動量
軸を取ったら次はベクトルの成分表示をしよう。軸と同じ向きなら正。逆向きなら負です。(ベクトルの扱い方はこちら)
\(\vec{P} = (\frac{h}{\lambda})\)
\(\vec{p_x} = (\frac{h}{\lambda’}\cos{\theta})\)
\(\vec{p_x’} = (mv\cos{\alpha})\)
後は運動量保存を使えばいい。
(はじめの運動量の和)+(外力からされた力積)=(あとの運動量の和)
今回、外力からされた力積は0なので、
\(\vec{P} = \vec{p_x} + \vec{p_x’}\)
成分を代入して
\(\frac{h}{\lambda} = \frac{h}{\lambda’}\cos{\theta} + mv\cos{\alpha}\)・・・②
鉛直方向の運動量
次は垂直方向です。手順はさっきと全く同じ。
\(\vec{p_y} = (\frac{h}{\lambda’}\sin{\theta})\)
\(\vec{p_y’} = (-mv\sin{\alpha})\)
んで、
(はじめの運動量の和)+(外力からされた力積)=(あとの運動量の和)より
\( 0 = \vec{p_y} + \vec{p_y’}\)
∴\( 0 = \frac{h}{\lambda’}\sin{\theta} – mv\sin{\alpha}\)・・・③
これで、運動量保存のしきが立てられました。
電子の情報は削除せよ
さ、この①~③式を使って波長差\(\Delta \lambda = \lambda’ – \lambda \)を求めるんだけど・・・
どっから手を付けたらいいのか・・・
ってなると思うので、こう考えてください。
コンプトン効果を考えていくときにどうしても知るのに困難な情報があります。
それは、電子の情報です
つまり、電子の速さ\(v\)と電子の偏角\(\alpha\)を知ることはまずできないってことだ。
だから、この二つを消去するっていう方針で式を変形してみよう。
一番に考えるべきは②と③にある\(\sin{\alpha}\)と\(\cos{\alpha}\)だ。
これを消去するには\(sin^2 \alpha + cos^2 \alpha = 1\)を使うしかない!!
なので、これを作り出すために②と③を二乗します。(それぞれ移項してから二乗します)。
\(\left(\frac{h}{\lambda} – \frac{h}{\lambda’}\cos{\theta} \right)^2 = (mv)^2 \cos^2{\theta}\)・・・②’
\(\left(\frac{h}{\lambda’} \right)^2 \sin^2{\theta} = (mv)^2\sin^2{\alpha}\)・・・③’
②’を展開して、この二つを足してあげると・・・
\(\left(\frac{h}{\lambda}\right)^2 – \frac{2h^2}{\lambda \lambda’}\cos{\theta} + \left(\frac{h}{\lambda’} \right)^2 \cos^2{\theta} + \left(\frac{h}{\lambda’} \right)^2 \sin^2{\theta} = (mv)^2 \cos^2{\alpha} + (mv)^2\sin^2{\alpha}\)
これをもう少しきれいにすると
\(h^2 \left(\frac{1}{\lambda^2} – \frac{2}{\lambda \lambda’} \cos{\theta}+ \frac{1}{\lambda’^2} (\sin^{\theta} + \cos^2{\theta} \right) = m^2v^2(\sin^2{\alpha} + \cos^2{\alpha}\)
\(\sin^2{x} + \cos^2{x} = 1\)を使って・・・
\(h^2 \left(\frac{1}{\lambda^2} – \frac{2}{\lambda \lambda’}\cos{\theta} + \frac{1}{\lambda’^2} \right) = m^2v^2\)
次に\(v/)を消したいので、①をこの式に代入します。
そこで①を\(m^2v^2 = OO\)の形にすると・・・
\(m^2v^2 = 2mhc\left(\frac{1}{\lambda} – \frac{1}{\lambda’} \right)\)
後は代入して\(\Delta \lambda\)を導こう。
\(h^2\left(\frac{1}{\lambda^2} – \frac{2}{\lambda \lambda’}\cos{\theta} + \frac{1}{\lambda’^2} \right) = 2mhc \left(\frac{1}{\lambda} – \frac{1}{\lambda’} \right)\)
両辺に\(\lambda \lambda’\)を掛けます。
\(h^2 \left(\frac{\lambda’}{\lambda} – 2\cos{\theta} + \frac{\lambda}{\lambda’} \right) = 2mhc(\lambda’ – \lambda )\)
さて、ここで、物理お得意の近似を使います。
コンプトン効果でX線の波長は変わるって言ってもほんのちょっとの変化です。だから\(\frac{\lambda}{\lambda’}と\frac{\lambda}{\lambda’}\)はそれぞれ1としていいわけだ。
つまり
\(h^2(2 – 2\cos{\theta}) = 2mhc\Delta \lambda\)
∴\(\Delta \lambda = \frac{h}{mc}(1 – \cos{\theta})\)
ってことで、波長はこれだけ変化するってことが分かるね。
以上コンプトン効果でした。
やっていることは今までやってきた力学のお話なので、演習のつもりでもう一度解いてみてください。