力学的エネルギー保存則とは？【9割が知らない真の公式】
どうも！オンライン物理塾長あっきーです
オンライン物理塾長あっきー
教科書読んでいたら、「運動エネルギーの変化量は、された仕事に等しい」って書いてあったり、「力学的エネルギーの変化量は非保存力にされた仕事に等しい」ってことも書いてあって・・・もうパニックです！
リケジョ志望のAIさん
今回はこの悩みを解決していきます。
教科書や参考書の説明には本当にこのような説明が多いんですよ。
「運動エネルギーの変化量は、された仕事に等しい」
「力学的エネルギーの変化量は非保存力にされた仕事に等しい」
「保存力のみが仕事する場合は力学的エネルギーは保存される」
ですが、これら3つには共通していることがあります。
仕事されればエネルギーが変化するということだけなんですね。
これがまさにエネルギー保存則です。
今回は、エネルギーと仕事の関係を見つめて、運動方程式からエネルギー保存則を導出していきます。
そして、上のようにわざわざ条件つけてパターン化するのではなく、たった1つの公式として成り立つ真のエネルギー保存則を教えていきます。
最後まで読めば、エネルギーと仕事の問題はすべて解けるようになります！
エネルギー保存則を運動方程式から導出できる
エネルギー原理（エネルギーと仕事の関係）が分かる
問題で使える真のエネルギー保存則の公式が分かる
仕事とは？
まず前提知識として、仕事とは何か説明していきます。
ある物体を一定の力Fで、その力の向きに距離xだけ動かしたとき、物体がされた仕事\(W\)は
\(W = Fx\)
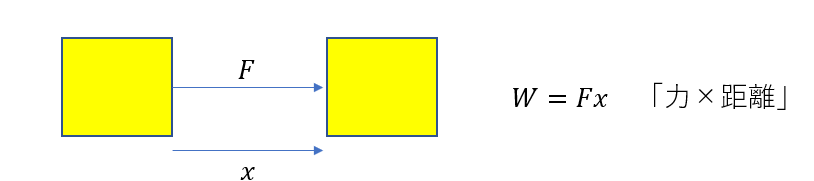
これにはいくつか注意があります。
仕事にはプラスマイナスがある
まず、仕事の正負の区別があります。
定義では「力の向きに」っていう一言があります。これを基準としているのです。つまり、
「力の向きに物体が動いたとき」→ 正
「力の向きと逆向きに動いとき」→ 負
力の向きと垂直に動いたとき→ ０
となります。
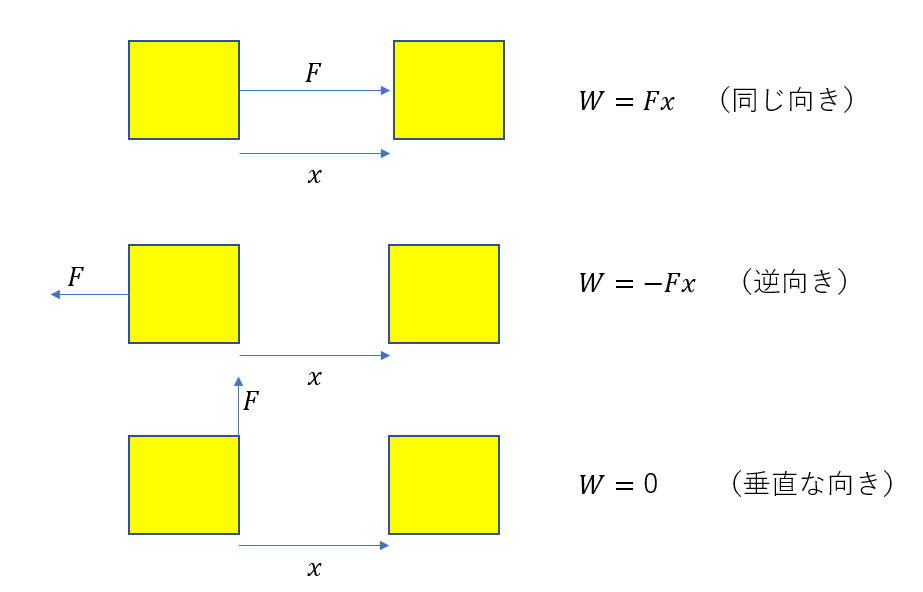
力が斜めに働く場合はどうするんですか？
リケジョ志望のAIさん
動く向きに対して、垂直と平行の向きに分解すれば平行向きの仕事だけ考えればいいですね。
オンライン物理塾長あっきー
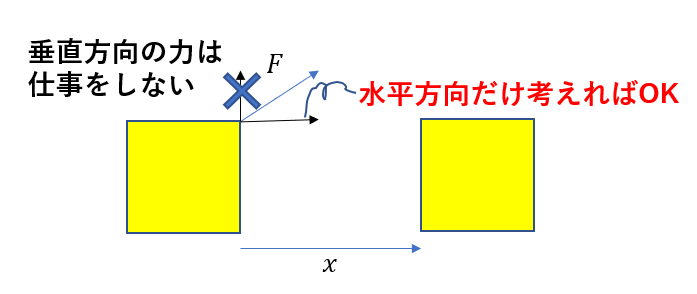
今は力の向きに動くかどうかでプラスマイナスを場合分けしていましたが、ベクトルを使うと場合分けせず一般化できます。
\(W = \vec{F}・\vec{x}\) （力と変位の内積）
軸を取ってプラスマイナスを考慮すれば出ますね。
ベクトルに関してはこちらに説明しているので確認してください。
力が一定じゃないときは「力×キョリ」としてはダメ
もう一個の注意点は
上の定義にあるように、「力が一定」のとき\(W = Fx\)と書けるのです。
もし力が変化するようなら、別の方法で求めないといけません。
その方法は、
F-xグラフ（力と距離の関係グラフ）の面積を求める！！
です。
これは積分を使わないと普通は解けないので、高校生のあなたは、一次関数の場合だけ面積で求められるようにしよう。
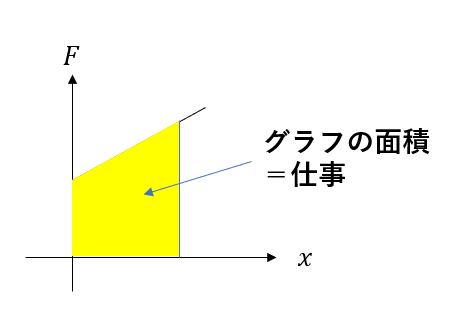
エネルギー保存則を導出しよう
ではここからエネルギー保存則について考えていきます。まず、エネルギー保存則を導出していきます。
図のように質量\(m\)の物体を大きさが\(F\)で右向きに一定な力を加え、その向きに\(\Delta x\)だけ動かす。物体の速さが\(v_0\)から\(v\)に変化したとき、仕事と運動エネルギーの関係を式に表せ。
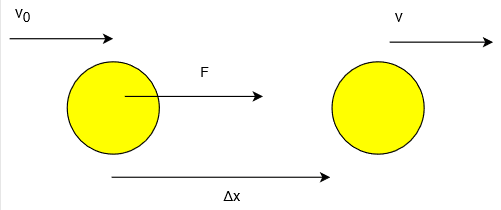
まず、この物体の運動方程式を立ててみます。
\(a = \frac{F}{m}\)
今回、\(F = 一定\)なので、\(a\)も一定ですね。
なので、等加速度運動することがわかります。
\(v^2 – v_0^2 = 2ax\)
を使ってみます。
仕事とエネルギーの基本式「エネルギー原理」
この式の右辺\(Fx\)は「力×距離」つまり物体がされた仕事です。
左辺は\(\frac{1}{2}mv^2\)という形の項がありますね。
これは運動エネルギーと言われていて、エネルギーの一種です。
左辺は「運動エネルギーの変化量」になっているので、「運動エネルギーの変化はされた仕事に等しい」ということが言えました。
これは教科書で説明されているエネルギーと仕事の関係です。
ですが覚えにくいので式変形します。
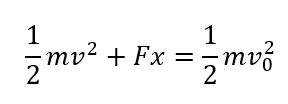
これは次のようにみなせます。
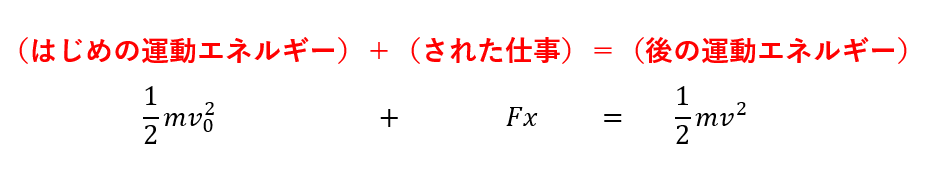
「仕事をされればエネルギーが増える」
ということを表している式なんです！
これはエネルギーと仕事の本質を表した式でエネルギー原理（エネルギー保存則）と言われています。
この公式さえ知っていればエネルギーと仕事の問題はなんでも解けてしまいます！
超重要公式なのでしっかり意味も含めしっかり覚えましょう！
＊運動エネルギーを先に定義して上の関係を満たすものを仕事と定義する見方もあります。大学ではこのように定義するのが一般的です。
力学的エネルギー保存則を導出してみよう
うそ！これだけ！「力学的エネルギー保存則」とかはいらないんですか？
リケジョ志望のAIさん
力学的エネルギー保存則もこのエネルギー原理から導けるから覚える必要はないよ。
オンライン物理塾長あっきー
エネルギー原理から力学的エネルギー保存則を実際に導出してみましょう。
図のように、質量\(m\)の物体が重力のみを受けて、高さが\(h_1\)から\(h_2\)まで移動する。このとき、物体の速さは\(v_1\)から\(v_2\)に変化した。物体の力学的エネルギー変化について考えよ。重力加速度の大きさは\(g\)とする。
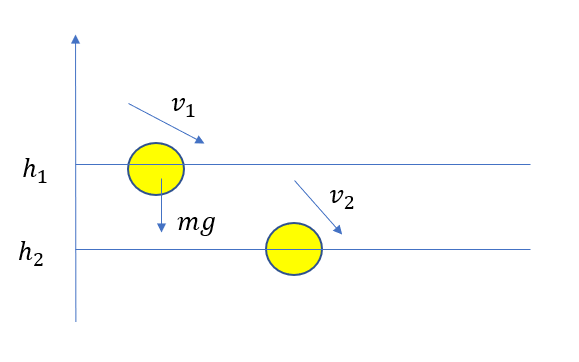
エネルギー原理は
（はじめの運動エネルギー）＋（された仕事）＝（あとの運動エネルギー）
という関係でしたね。それぞれの情報を整理するとこうなります。
はじめの運動エネルギー・・・\(\frac{1}{2}mv_1^2\)
された仕事・・・\(mg(h_1 – h_2)\) （重力は一定なので「力×距離」でOK）
あとの運動エネルギー・・・\(\frac{1}{2}mv_2^2\)
これを関係式に当てはめていきます。
力学的エネルギー保存則の公式
両辺とも
\(\frac{1}{2}mv^2 + mgh\)
という形になっていますね。
\(\frac{1}{2}mv^2\)は先ほど見たように運動エネルギーでした。
\(mgh\)は（重力による）位置エネルギーというエネルギーの１つです。
位置エネルギーに関しては最後に補足として教えます。
つまり、
\(\frac{1}{2}mv^2 + mgh\)
は「運動エネルギー＋位置エネルギー」という形になっています。
この形のエネルギーを力学的エネルギーと呼びます。
なので、この式をよく見てみると・・・
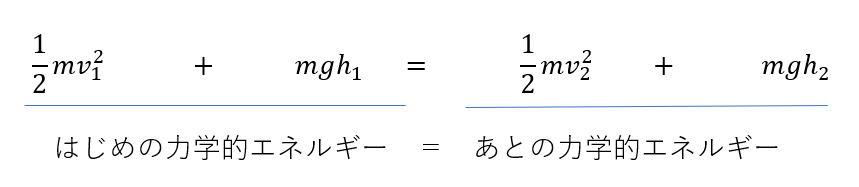
つまり・・・
力学的エネルギー＝一定！！
です。
これが「力学的エネルギー保存則」です。
力学的エネルギー保存則は保存力のみが仕事をする場合のみ
この保存則には一つ注意があります。
これが成り立つのは「保存力」だけが仕事をする場合です。
保存力とは以下の3つだけを押さえておけばOKです。
- 重力
- ばねの弾性力
- 静電気力
じゃあ、保存力以外の力（非保存力）が仕事をしたらどうなるんですか
リケジョ志望のAIさん
いい質問だね。それを最後に考えて終わりにしよう！
オンライン物理塾長あっきー
問題で使えるエネルギー保存則とは？
では、非保存力から仕事をされる場合を考えてみましょう！
図のように、質量\(m\)の物体を摩擦のある斜面を下る運動を考える。高さ\(h_1\)の時の速さを\(v_1\)、高さ\(h_2\)の時の速さを\(v_2\)とし、物体が斜面上を動いた距離を\(L\)とする。動摩擦係数を\(\mu\)、重力加速度の大きさを\(g\)として、エネルギーと仕事の関係について考えよ。
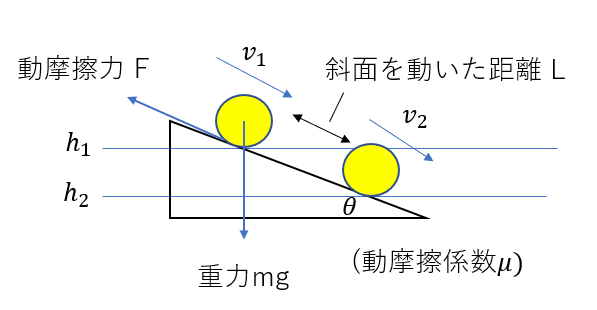
さっきと全く同じように、エネルギー原理を使います。
はじめの運動エネルギー
\(\frac{1}{2}mv_1^2\)
された仕事
重力にされる仕事 ：\(W_g = mg(h_1 – h_2)\)
動摩擦力にされる仕事：\(W_F = -\mu mg \cos{\theta} L\)
（動摩擦力による仕事は力の向きと移動する向きが逆なので、マイナスになるところは注意！）
あとの運動エネルギー
\(\frac{1}{2}mv_2^2\)
エネルギー原理の公式にこれらを当てはめます。
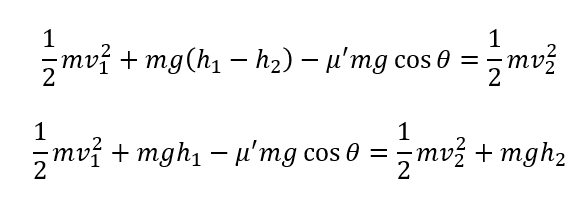
真のエネルギー保存則
おそらくイメージ通りだったと思います。
こういう関係になっているんですね。これもエネルギー原理と同様に
「仕事をされればエネルギーが変化する」
ということを表しているだけにすぎないんです。
この非保存力にされた仕事が０ならさっきの力学的エネルギー保存則になるんですね！
リケジョ志望のAIさん
そう！だから力学的エネルギー保存則をわざわざ覚える必要はないんだ。
オンライン物理塾長あっきー
これが真の意味で「エネルギー保存則」なんです。
もちろんエネルギー原理から導けるので覚える必要は本当はありません。しかし、それだと計算が複雑になり、時間がかかったり、計算ミスも起こりやすいです。
導出して意味を理解した上でこの真のエネルギー保存則も覚えておくといいでしょう。
位置エネルギーと保存力
最後に位置エネルギーという言葉があったのでこちらを説明しましょう。
位置エネルギーというのは簡単に言うと
「保存力のした仕事」
のことです。
保存力は3つしかありません。
- 重力
- ばねの弾性力
- 静電気力
それぞれがした仕事が位置エネルギーとして表されます。
重力による位置エネルギー
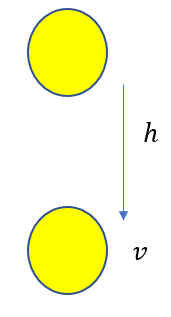
例えば高さ\(h\)のところから静かに物体をはなし、落ちたところで速さ\(v\)となったとすると
エネルギー原理から
\(o + mgh = \frac{1}{2}mv^2\)
となりますね。
右辺は運動エネルギーということなどで、左辺の\(mgh\)も、本当は重力のした仕事なんだけど一種のエネルギーとしてみなしましょうと考えたいんですね。
そこでこの\(mgh\)を重力による位置エネルギーとするわけです。
弾性力による位置エネルギー
ばねの場合も同様です。
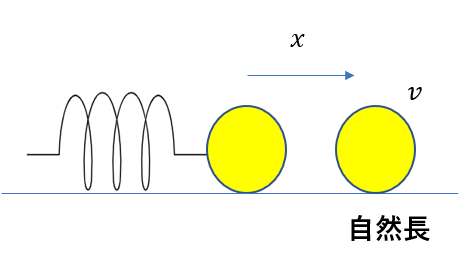
自然長から\(x\)だけ縮んだ状態で自然長までばねが仕事をして、速さ\(v\)になったとして
同じようにエネルギー原理を考えてみましょう。
ある位置\(x\)での弾性力の大きさは\(kx\)なので、エネルギー原理を使えば
\(0 + kx \times x = \frac{1}{2}mv^2\)
・・・
とはなりません！
今回の力\(kx\)は一定じゃないですよね？
ばねの弾性力はばねの伸びた長さで決まるわけですから、今回は変化していきます。
つまりF-xグラフの面積を求めないといけないわけです
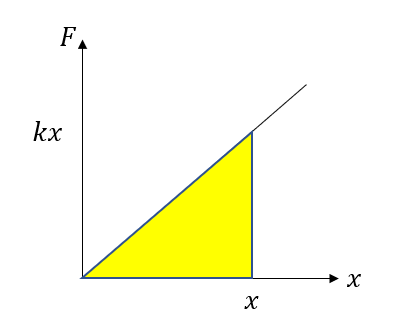
\(F = kx\)は直線のグラフなので、この面積は簡単に求められますね。
\(\frac{1}{2}kx^2\)です。
ということで改めてエネルギー原理を使うと
\(0 + \frac{1}{2}kx^2 = \frac{1}{2}mv^2\)
となりますね。
先ほどと同じように
\(\frac{1}{2}kx^2\)は弾性力の仕事なんですけど、エネルギーとして扱った方が都合がいいので、
これを弾性力による位置エネルギーとよびます。
静電気力（電場）による位置エネルギー
これも同じですが、そもそも静電気力や電場についての知識が必要なのでこちらの記事を参考にしてください。
位置エネルギーは基準を決める
これら位置エネルギーは基準が設定できます。
重力の位置エネルギー\(mgh\)の\(h\)は「基準点からの高さ」を表します。
基本は物体の運動の中の最下点を基準に取るのが普通です。
基準を取るので、場合によってはマイナスになることもあります。
基準より上にあればプラス
基準より下にあればマイナス
になることには注意してください。
エネルギー保存則は何も難しくない
いかがでしたか？
これさえきちんと理解しておけばどんな問題でも解くことができます。
さっそく問題集を開いて、1問でも良いので実際にこれを使って解いてみましょう！
↓問題演習はこちら↓
オンライン物理塾長あっきーからのお知らせ！
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます！今ならすごいサポート特典もあります！
＊無料の物理攻略合宿よりも充実のコンテンツです！
