【高校物理】エネルギー保存則の力学の問題。やるべきはたった1つ?

18:46:28どうもです。
エネルギーと仕事の問題、私すごい得意になりました。だって公式一つですらすら解けるんですもん!
 AI
AI
その感覚良いね!じゃあ、今回問題出すから解いてみてよ!
 AKINORI
AKINORI
ということで、AIさんがエネルギーと仕事の問題を
たった一つの公式で解くそうです。
注目です!!
まずはチェック
問題
図のようなレールを考える。レールは最下点では滑らかにつながっており、最下点ではレールは水平である。最下点の水平なレールの一部では摩擦が働く。この区間をBCとする。BCの長さを\(L\)、動摩擦係数を\(\mu’\)、重力加速度の大きさを\(g\)として以下の問いに答えよ。ただし、区間BC以外では摩擦は働かないとする
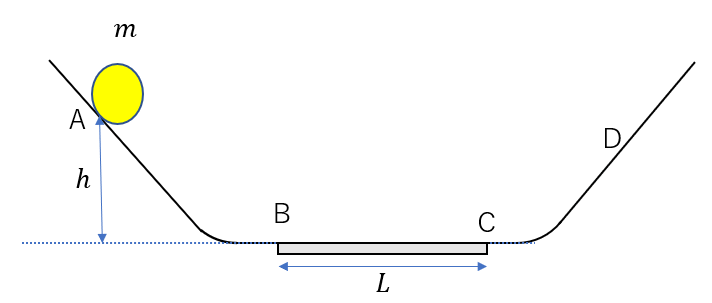
(1)高さ\(h\)の点Aから質量\(m\)の物体を静かに置く。物体はBCを通過し、右側のレール上で最高点Dに達した。このDの高さを求めよ
(2)物体はBCを何回か通過するが、最終的にBC上のある点で静止した。その位置を求めよ。ただし、\(2\mu’ L < h < 3\mu’ L\)とする。
(1)「エネルギー保存則」これだけ
こんなの楽勝ですよ!エネルギー保存則を使えば終わりですよね
 AI
AI
その通り!
 AKINORI
AKINORI
エネルギー保存則とはこの式でした。
(はじめの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
もうこれを使うしかないですね。
エネルギーと仕事の問題が出てきたら真っ先にこの関係式を思い浮かべましょう。
(*エネルギー原理で考えるのもOK)
もちろん、これを適用するには情報をそろえる必要がありますね。
ということで、まずは情報収集です。
位置エネルギーは最下点を基準に取りましょう。
- はじめの力学的エネルギー・・・\(mgh\)
- あとの力学的エネルギー・・・\(mgh_1\)
- 非保存力にされた仕事・・・\(\mu’ mg・L\)
今回、はじめは速度が無いので、位置エネルギーだけ考えればいいですね。
また、Dに達したときこれは「最高点」ですから、もちろん速度は0です。
なのでこれも位置エネルギーだけ考えればいいんですね。そして、高さを求めたいので\(h_1\)とおきます。
そして非保存力にされた仕事。
今回、仕事する非保存力は動摩擦力です。
動摩擦力は大きさが
\(F_r = \mu’ N = \mu’ mg\)
です。
そして、向きは
物体が動く向きと逆
です。
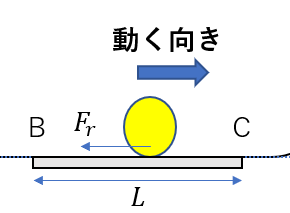
なので、非保存力にされた仕事は
\(W = – \mu’ mg ・L\)
ですね。
ということで情報がそろいました。
あとは
(はじめの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
これに当てはめるだけです。
\(mgh + (-\mu’ mg・L) = mgh_1\)
∴\(h_1 = h – \mu’ L\)
これが答えです。

(2)エネルギー保存則から状況を理解する
どんな問題がきても同じですよ!エネルギー保存則使えばいいんですよね!?
 AI
AI
その通りですよ!ただ、今回はいつ止まるかが重要になってくるよ
 AKINORI
AKINORI
物体は最初Dに達した後、再び区間BCに到達します。
ですが、次に通過するかどうかはわかりません。
また、次の次も通過するかどうかもわかりません。
こうやって、BCに差し掛かるたびに「本当に通過するの?」というのを考える必要があります。
だから\(h\)には条件があるんですね。
 AI
AI
その通過するかどうかを決めるのがこの\(h\)の条件なわけですね。
まず、Dに到達した後、BCを通過するかを考えます。
通過すると考えて同じようにエネルギー保存則を立ててみます。
(はじめの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
- はじめの力学的エネルギー・・・\(mg(h – \mu’ L)\)
- 非保存力にされた仕事・・・\(\mu’ mg L\)
- あとの力学的エネルギー・・・\(mgh_2\)
ということで
\(mg(h – \mu’ L) + (- \mu’ mgL) = mgh_2\)
∴\(h_2 = h – 2\mu’ L\)
今回\(2\mu’ < h\)
という条件から
\(h_2 > 0\)
ですね。
これは「BCを通過しある高さ\(h_2\)まで登る」
ということを意味しています。
とにかく、この場合通過できたってわけです。
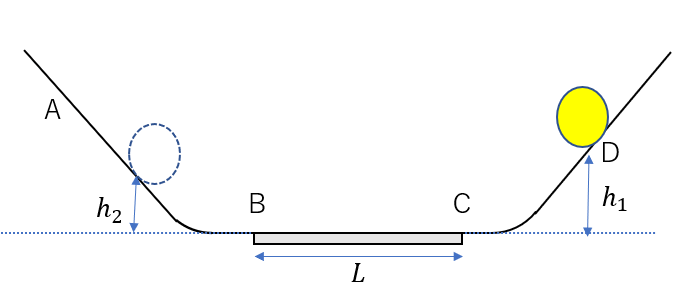
今度も全く同じように三回目(図の\(h_2\)の高さから)BCを通過できるかを考えていきます。
もう、計算しなくてもだいたい予想着きますよね。
仮に、BCを通過できるとすれば
\(h_3 = h – 3\mu’ L\)
の高さまで達するはずです。
なんですが、\(h < 3mu’ L\)
ですので、\(h_3 < 0\)
です。
さて、高さがマイナスとはどういうことでしょう。??
最下点より下??
・・・・・
ありえません!!

なので、そもそも通過できないってことです。
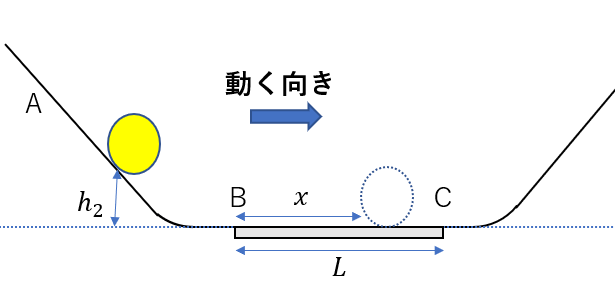
その都度通過するか考えていたのは、Bから入って止まるかCから入って止まるかで、止まる場所が変わりますよね。
ですので、こうやって一回一回通過するかどうかを考えて行きました。
あとは全く同じようにエネルギー保存則を使います。
今回、Bから入るのが分かるので
Bから\(x\)だけ進んだところで止まったとしましょう。
(はじめの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
- はじめの力学的エネルギー・・・\(mg(h – 2\mu’ L)\)
- 非保存力にされた仕事・・・\(-\mu’ mg x\)
- あとの力学的エネルギー・・・0
ということなので
\(mg(h – 2\mu’ L) + (-\mu’ mgx) = 0\)
∴\(x = \frac{h}{\mu’} – 2L\)
となりますね。
つまり答えは
「Bから右に\(x = \frac{h}{\mu’} – 2L\)位置」
です。
やっぱりエネルギー保存則(もしくはエネルギー原理)を使えば終わりなんですね。
 AI
AI
そうだね。ただ、物理は公式を当てはめればOKではなく、その式から状況を解釈することも重要なんだ。(2)みたいなやつね。でもAIさん、かなり理解できてます!
 AKINORI
AKINORI
ということで、結論
エネルギー保存則(もしくはエネルギー原理)をつかえ!!








