二体問題を重心で攻略!大学入試で差がつく解き方を大公開!

Akinoriさん。今日は二体問題の演習をやりたいです。
 AI
AI
わかった。実際にやってみよう。結構内容が濃いから頑張ってついてきてね
 AKINORI
AKINORI
まずはチェック
必ずこの記事を読んでから問題に取り掛かって下さい!
目次
問題
水平面上に、なめらかな溝をもつ直線のレールがある。この溝の中に、質量\(M, m\)の小球A,Bを置き、両者ばね定数\(k\)のばねでつないだ。ある瞬間に、Aを大きさ\(v\)の右向きの速度を与えると、その後、AとBは、振動しながら全体として右向きに進んでいく。次の各問に答えよ。
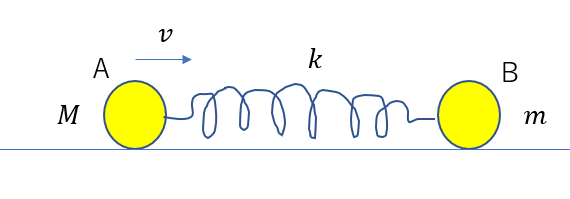
(1)AとBをまとめて一つの物体とみなしたとき、その重心の速度の大きさを求めよ
(2)重心から見たBの運動は単振動になる。その周期を求めよ
(3)ばねの伸びの最大値を求めよ
(セミナー物理基礎・物理 2016, 問223改)
もちろんポイントは別記事で紹介した通りです。
(1)重心速度は重心位置から
これは重心速度の導出そのものですね。
重心速度は重心位置を求めることで導けます。
「まずはチェック」でも説明していますが、問題なのでもう一度導出します。
重心は「重力の代表点」だから
- 全重力は重心にかかる
- モーメントも重心の重力が代表する
ってことですよね。
 AI
AI
いいね!理解できてるよ
 AKINORI
AKINORI
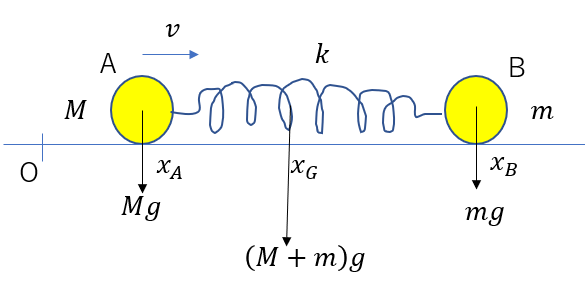
重心には大きさ\((M + m)g\)の重力がかかっていて
この重力のモーメントは、各重力のモーメントを代表しているわけですね。
原点周りのモーメントを考えると
\((M + m)g・x_G = Mg・x_A + mg・x_B\)
∴\(x_G = \frac{Mx_A + mx_B}{M + m}\)
ここでは、ベクトルを強調しておきます。
\(\vec{x_G} = \frac{M\vec{x_A} + m\vec{x_B}}{M + m}\)
そして、位置についてこの関係が言えるんだから、速度についても言えそうだな~
っていうことで重心速度も同じ形になります。
\(\vec{v_G} = \frac{M\vec{v_A} + m\vec{v_B}}{M + m}\)
こういうイメージが嫌いな人は両辺を微分してみてください。
位置を微分すると速度になるので、確かにこの式が得られますね。
さて、ここで分子を見るんですね。\(M\vec{v_A} + m\vec{v_B}\)は運動量の和ですよね!!
 AI
AI
なんか張り切ってるね・・・
 AKINORI
AKINORI
\(M\vec{v_A} + m\vec{v_B}\)は運動量の和ですが、
今回、内力しか働いていませんね。
物体A,Bがばねを介して力を及ぼしあっているのが内力です。
ってことは・・・
\(M\vec{v_A} + m\vec{v_B} = 一定\)
ということです。
つまり、最初の運動量が分かれば後はその値でずっと同じということです。
なので、最初の運動量を考えてみましょう。
最初では
\(\vec{v_A} = \vec{v} = (v)\)
\(\vec{v_B} = 0\)
ですよね。
つまり、最初の運動量は
\(M\vec{v}\)
ということです。
ということで、重心速度は
\(\vec{v_G} = \frac{M}{M + m}\vec{v}\)
ただ、今回は速さを答えないといけないので成分を代入したものを答えます。
\(\vec{v_G} = \frac{M}{M + m}v\)
ここは大丈夫です!
 AI
AI

(2)重心から見た運動をどう考える??
ここが全然わからないです。解説読んでも意味わかりません!!
 AI
AI
ここはじっくり説明していこう
 AKINORI
AKINORI
ここはかなりハードです。頑張ってついてきてください。うまく式を解釈する必要があるので。
まず、重心から見たBの運動は単振動になる。
これは大丈夫ですね。問題文にも書いてありますが、書いてなくても理解しておきましょう。
そして、単振動の周期を考えるには運動方程式を立てる必要がありますね。
その際にはBに働く合力、特に
ばねの弾性力
を求めないといけないわけですよ。

ばねの弾性力を求める
でも、これ厄介じゃありません?物体が一つだったらばねの伸びは考えやすかったけど、今回二つ物体があってそれぞれ振動するからばねの伸びが分からないですよね?
 AI
AI
そうなんだ。そこをここから考えていくよ
 AKINORI
AKINORI
例えば、次のような弾性力は求めるのは難しくないんですよ。
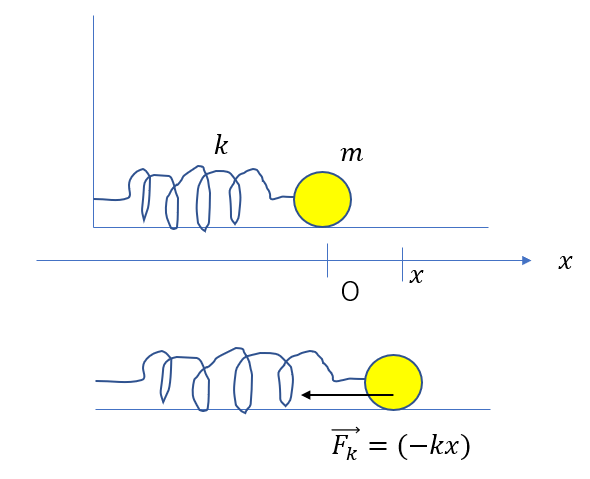
だって、物体の位置がそのままばねの伸び(縮み)になってくれるからね。
でも今回はそうはいかないですよね。
そこを式で理解していく必要があります。
ではいきましょう。ここから頑張ってついてきてくださいね。
まず、ばねの自然長の長さが\(L\)であるときの物体の座標を表しておきます。
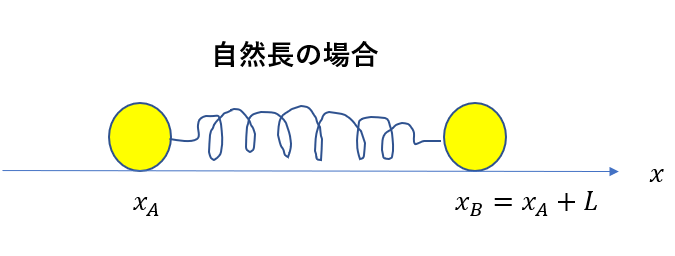
まあ、こうなりますよね。
そして、ここから
物体Aが\(x_A’ = x_A + \Delta x_A\)
物体Bが\(x_B’ = x_B + \Delta x_B\)
だけ変位したとします。この\(\Delta x_B\)は変位なので、プラスにもマイナスにもなり得ます。
プラスのときは右向きに動く
マイナスのときは左向きに動く
ということです。
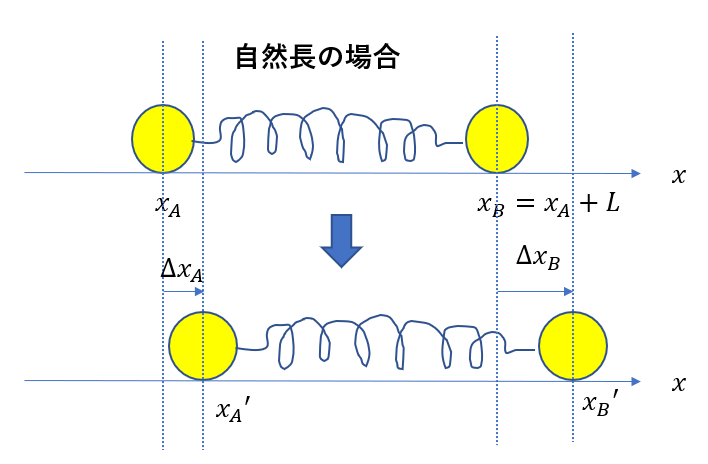
図を見ると、
\(\Delta x_B\)だけばねが伸びて
\(\Delta x_A\)だけばねが縮んでいる
こと分かりますね。
つまりこの時のばねの伸びは
\(\Delta x_B – \Delta x_A\)
ですね。
ということは、B(A)が受ける弾性力の大きさは
\(F_k = k(\Delta x_B – \Delta x_A)\)
ですね。
さて、弾性力は力なので\(\vec{F_k} = (〇)\)という風に成分表示したいと思います。
これについてはこちらから
- \(\Delta x_B – \Delta x_A > 0\)のとき
これは「Bの伸びの方が大きい」ということなので、ばね全体は伸びています。
そうすると、Bは左向きに力が働くので
\(\vec{F_k} = (-k(\Delta x_B – \Delta x_A))\)
となりますね。
- \(\Delta x_B – \Delta x_A < 0\)のとき
今度は「Aの縮みの方が大きい」ということなので、ばね全体は縮んでいます。
そうすると、Bには右向きに力が働くので
\(\vec{F_k} = (-k(\Delta x_B – \Delta x_A))\)
となりますね。
結局、ばねが伸びようが縮もうが
\(\vec{F_k} = (-k(\Delta x_B – \Delta x_A))\)
と表されることが分かりました。
これをもう少し変形します。
\(\Delta x_B – \Delta x_A\)
\(=x_B’ – x_B – (x_A’ – x_A)\)
\(= x_B’ – x_A’ – (x_B – x_A)\)
\(x_B – x_A\)は自然長の長さLでしたから
\(x_B’ – x_A’ – L\)
と書けます。
なので、ばねの弾性力は
\(\vec{F_k} = (-k(x_B’ – x_A’ – L))\)
と表せますね。
*ちなみに
\(x_B’ -x_A’\)は「Aから見たBの位置」という意味ですから
これは「Aに乗ってBを見る」あの相対系の話をしていることが分かりますね。
相対系についてはこちら!
重心から見たBについて考える
・・・あれ?全然重心を使ってないじゃないですか!
 AI
AI
確かに、ここまではね。ここから、重心から見た運動に変えていきます。ポイントはさっきの弾性力からAを消すことです。
 AKINORI
AKINORI
ここから、「重心から見たBの運動」を考えていきたいのですが、
弾性力では\(x_A’\)のようにAの情報が入っていますよね。でも、「重心から見たBの運動」を考えるには
Aの情報ではなく重心の情報が欲しんですよ。
そこで、重心の情報を入れるために式変形していきます。
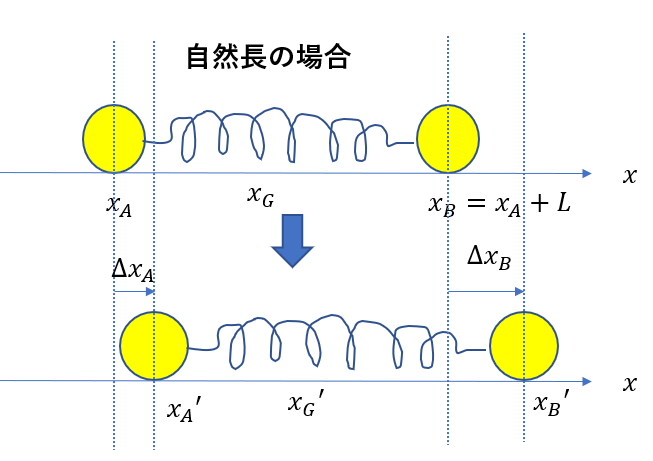
さっきの図に重心を書いておきました。
最初にやったのと同じ方法で\(x_G’\)は導けます。
\(x_G’ = \frac{Mx_A’ + mx_B’}{M + m}\)
「重心から見たBの運動」としたいので
「(Bの情報)-(重心の情報)」
というのが欲しんですよ。
なので、今回の場合\(x_B’ – x_G’\)を出します。これは普通に計算します。
\(x_B’ – x_G’ = \frac{M}{M + m}(x_B’ – x_A’)\)
∴\(x_B’ – x_A’ = \frac{M + m}{M}(x_B’ – x_G’)\)
これをさっきの弾性力に代入します。
ちょっとごちゃごちゃするので、成分(()の中身)だけを見ます。
\(-k(\frac{M + m}{M}(x_B’ – x_G’) – L)\)
∴\(-\frac{M + m}{M}k(x_B’ – x_G’ – \frac{M}{M + m}L)\)
はい!できました。
・・・え?何が?全然意味が分からないんですが・・・
 AI
AI
じゃあ、変形前のものと見比べてみましょう
 AKINORI
AKINORI
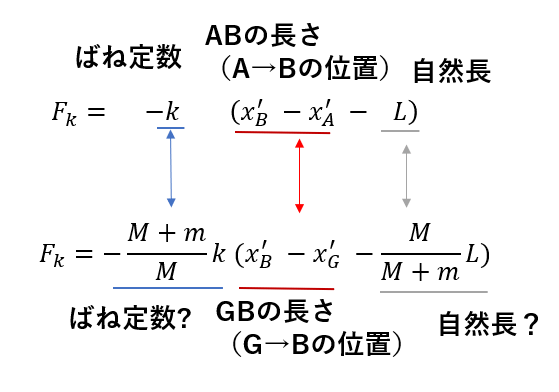
ごちゃごちゃしててごめんなさい 🙇
最初、重心で考える前の弾性力と
今出した弾性力とを見比べてみてください。
- k(ばね定数)→\(\frac{M + m}{M}k\)
- \(x_B’ – x_A’\)(B→Aの位置)→\(x_B’ – x_G’\)(G →Bの位置)
- \(L\)(自然長)→\(\frac{M}{M + m}L\)
という風に対応しているのが分かりますよね。
特に\(x_B’ – x_G’\)があることで、重心から見たBの運動を考えていることが分かります。
そして残りのものを考えると、重心から見たBの運動について次のようなことが言えるわけです。
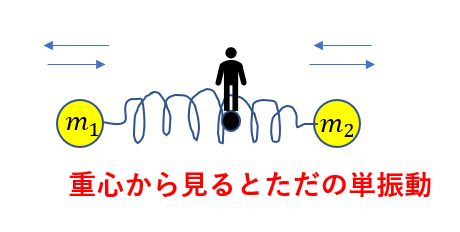
ばね定数が\(\frac{M + m}{M}k\)で自然長が\(\frac{M}{M + m}L\)のばねによる単振動!!

これを図にすればこうなるんです。
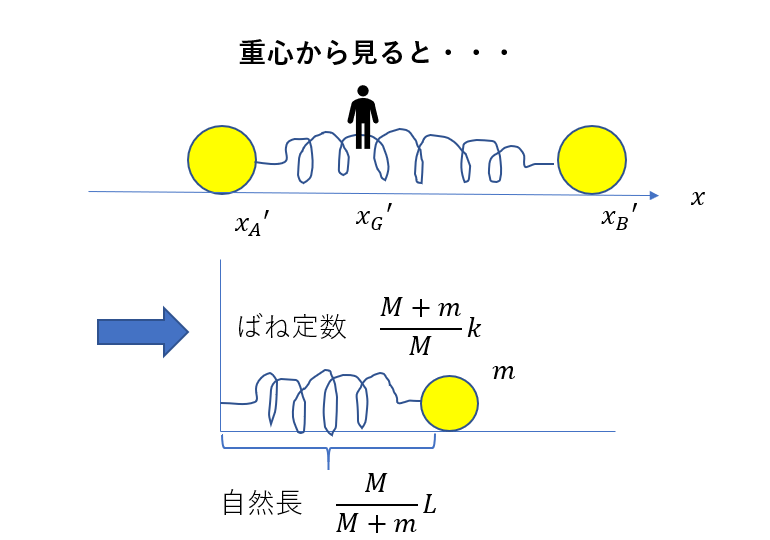
うわ!すごい単純!!これなら周期も簡単に求められそう!
 AI
AI
ここまでくるのは大変だったけど、式を変形して解釈することでここまで単純化できるわけです。
 AKINORI
AKINORI
あとは運動方程式を立てるだけ
あとは、運動方程式を立てるだけです。
単振動の運動方程式を立てる流れはこちらを確認してください。
この記事通りにやってみてください。
自然長を原点にとれば楽勝です。
簡単な解説だけします。
弾性力は\(\vec{F_k} = (-\frac{M + m}{M}kx)\)なので、
あとは運動方程式を\(m\vec{a} = \vec{F}\)に成分を代入すれば
\(ma = -\frac{M + m}{M}kx\)
∴\(a = -\frac{M + m}{Mm}kx\)
となって、
\(a = – (定数)×(xの一次式)\)という
形になりましたね。なので、単振動するということが分かります。
単振動すると分かったらやるべきことが3つありました。
- 中心の位置
これは原点です。(明らか)
- \(\omega \)の値
\(\omega = \sqrt{定数}\)ということなので
\(\omega = \sqrt{\frac{M + m}{Mm}k}\)
- 周期\(T\)を求める
これがまさに答えになりますね
\(T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{Mm}{(M + m)k}}\)
うわ~~!きつすぎです!!
 AI
AI
でも、問題集の解説じゃ物足りなかったんでしょ。しかもまだ、(2)だよ(笑)。
 AKINORI
AKINORI
・・・・・
 AI
AI

(3)エネルギー保存を使ってみよう
エネルギー保存則を使って解いてみましょう!((2)よりははるかに楽なので大丈夫です(笑))
重心を使った力学的エネルギーは大丈夫ですよね?
(力学的エネルギー)=
(重心エネルギー)+(内部エネルギー)
また内部エネルギーは
(内部エネルギー)
=(重心からみた運動エネルギー)+(弾性エネルギー)
でした。
さて、ここで考えたいのは
「ばねが最大まで伸びたときってどんな状況?」
ってことですよね。
例えば、重心から見たBやAの速度が0じゃなかったらどうでしょう?
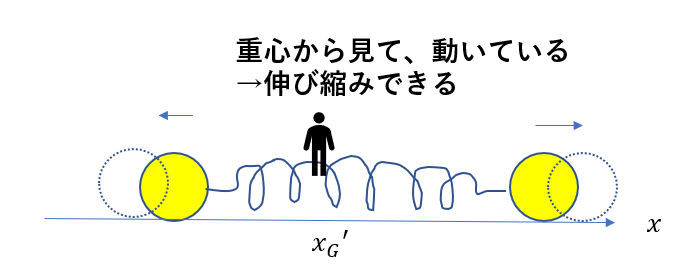
どう見ても最大じゃないですよね。速度を持っているってことはまだ動けるってことですから。
つまり、ばねの伸びが最大になるのは
重心から見て止まったとき!!
です。
ですからエネルギーを考えたときに・・・

こうなりますね。
この時の\(x\)の最大\(x_{Max}\)を考えれば良いんです。
また、今回非保存力は仕事しないので、
(力学的エネルギー)=一定
ですね。
ですから最初の力学的エネルギーを求めればOKです。
最初の力学的エネルギーは
\(E = \frac{1}{2}Mv^2\)
ですね。
ということで
\(\frac{1}{2}Mv^2 = \frac{1}{2}(M + m)v_G^2 + \frac{1}{2}kx_{Max}^2\)
\(x_{Max} = v\sqrt{\frac{Mm}{(M + m)k}}\)
これが答えです
*もし、「速さの最大は?」となったら今度はばねが自然長になることが分かればこれもエネルギー保存で解けます。
疲れた!二体問題って難しいですね
 AI
AI
そうだね。今回はきつかったね。でも二体問題は大学入試で絶対に差が開く問題だから対策はしておこう!お疲れ様!
 AKINORI
AKINORI