知らなきゃ落ちる!二体問題の難問を重心で解く方法を公開します!

二体問題の解き方が分かる
重心を使った解法が理解できる
難関大を目指す人にとって、絶対に立ちはだかる壁があります。それは・・・
「二体問題」
です。
この二体問題の解き方が全く分からなくて、調べてみてもいまいちピンと来なかったりしませんか?
実は二体問題では重心を使った最強の解法があるのを知っていますか?
これは、教科書では語られていない、重要なもので僕はこれに関して非常に深く学んだ経験があります。
この記事では、入試最難関である二体問題を重心を使って解く方法をどこよりも分かりやすく説明してきます。
これは知っているか知らないかで点数を取れるかどうかが決まってしまいます。
最後まで読むことで、初見で二体問題が出てきてもすらすら解くことができます。
目次
そもそも二体問題とは!?

二体問題というのは「二物体の運動を追う」問題です。
二体問題のタイプは2つあって、一つは普通に解けるものです。
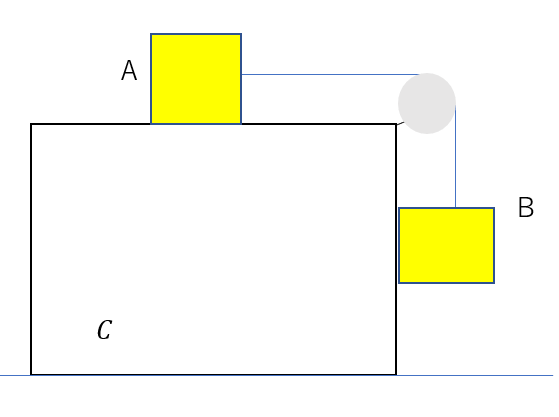
こんな感じで糸でつながっている問題は、特に難しくないです。
ですが、厄介なのがもう一つのタイプです。
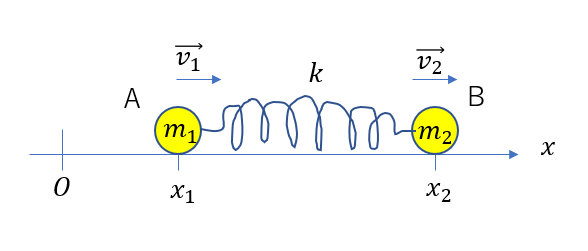
このように、ばねで繋がった2物体の問題が異常に難しいんです!
二物体がばねで振動しながら、全体としては右向きに運動するような。
そんな感じの運動です。
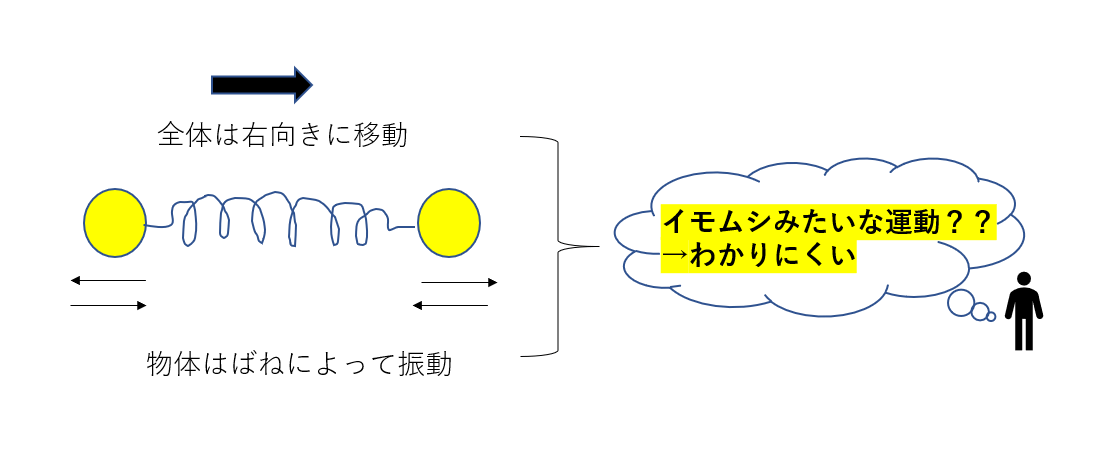
なんかイモムシみたいな運動ですね(笑)
このタイプの問題は、ある裏ワザを使うことで簡単に解くことができます。
というより、裏ワザを使わないと普通に詰みます!!
なので、しっかり理解してくださいね。
二体問題の解き方:「重心を使う」

図のように質量が\(m_1, m_2\)の物体A,Bがばね定数kのばねでつながれている。Aの座標が\(x_1\)のときの速度を\(\vec{v_1}\)、Bの座標が\(x_2\)のときの速度を\(\vec{v_2}\)とする。この時、重心の座標を求め、重心からみたとき二つの物体がどんな運動をするか考えよ。

結論からいいます。二体問題は
「重心を考える」
これが攻略法です!!
重心そのものの運動を見る
重心から見た個々の物体の運動を見る
この2ステップで必ず解くことができます。
重心って・・・あのモーメントに出てくるやつですか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
そう。重心はモーメントのところで習うと思いますが、この重心はモーメント以外でとても重要な役割を持っているんですね。
 あっきー
あっきー
この2ステップについて分かりやすく説明していきます。少し長くなりますが、頑張ってついてきてください!
なぜ重心を使って2ステップを考えるのか?

なんで「重心」と「重心から見た個々」に分けて考える必要があるんですか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
いい質問だね。これは運動を単純化するためのプロセスなんだ。
 あっきー
あっきー
今回の状況は運動をイメージしたところで何もできません。複雑すぎて、それぞれ運動方程式を立ててもその先に進まないのです。
ですが、この運動は2つの運動の組み合わせだということに気づければ一気に難易度が下がります。
その二つは
・全体の運動
・個々の運動
です。
全体の運動というのは、「物体とばねが全体的に右に進んでいる」という直線運動にすぎません。
個々の運動というのは、「各物体が振動している」という単振動にすぎません
つまり、この2つの運動に分けることで単純化することができるのです。
そこで登場するのが「重心」ということなんですね。
全体の運動というのは「重心の運動」のことであり
個々の運動は「重心から見た個々の運動」のことです。
なので、最初に紹介した2ステップを踏むことが二体問題の攻略のカギなのです。
ということで、それぞれの運動を見ていきましょう!
重心の運動を考える=全体の運動を考える
まずは重心の運動を考えるために、まずは重心の位置を求めてみましょう。
重心の求め方はこちらで詳しく解説していますのでチェックしてくださいね。
重心の位置を求める
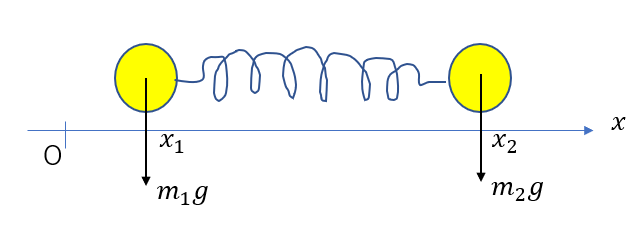
重心の位置を\(x_G\)とすると、重心は「重力の代表点」だからすべての重力がこの一点にかかっている!と見なせるんでしたね。
なので重心には
\((m_1 + m_2)g\)
の大きさの重力がかかっていて、なおかつモーメントも代表できる。
原点周りのモーメントを考えると・・・
(重心の重力のモーメント)=(各重力のモーメントの和)
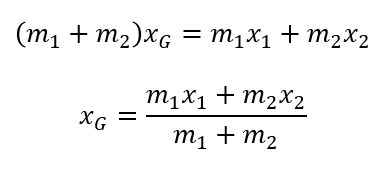
これが重心の位置です。
これは覚えるものではありません。導出をしてくださいね。
重心の速度を求める

ここから重心の速度についてみていきます。実は重心の速度にはある特徴があるんです。
重心の速度も同じように書けるのな?
 リケジョになりたいAIさん
リケジョになりたいAIさん
鋭いですね。実際そうなります。
 あっきー
あっきー
位置と速度、さらには加速度には以下のような関係がありました。
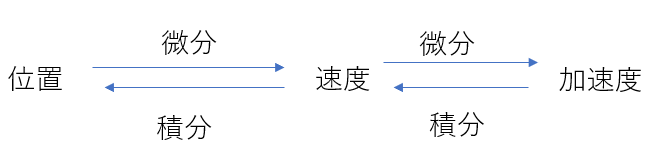
位置を微分したら速度になります。
上の式は複雑そうに見えますが、ただの足し算です。なので、微分をしても形は変わりません。
\(x_1, x_2\)がそれぞれ\(v_1, v_2\)に変わるだけです。
したがって、重心の速度\(\vec{v_G}\)は
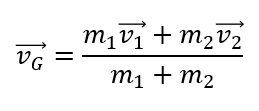
このように表されます。
もちろん加速度も同じように表されます。ただ使い道はゼロです(理由は後程)。
重心速度は一定!?

この重心の速度ですが、実は大きな特徴があります。
\(\vec{v_G}\)の式の分子をよく見てください。
\(m_1\vec{v_1} + m_2\vec{v_2}\)
この形を見て何か思いつきませんか?
あ!これ、運動量ですね!
 リケジョになりたいAIさん
リケジョになりたいAIさん
まさにこれは、2物体の運動量の和なっています
そして、この2物体は水平方向にのみ動いていて、水平方向にはばねの力しか働いていません。
このばねの力は・・・そうです、内力です!!
つまり運動量保存則を使えば、
\(m_1\vec{v_1} + m_2\vec{v_2} = 一定\)
ということになりますね。
もうお気づきですね。
もう一度\(\vec{v_G}\)を見てみましょう。

このように分母分子ともに一定なので
右辺が一定なわけです。
つまり
\(\vec{v_G} = 一定\)
なのです。
これは重心速度が一定ということ、つまり
重心は等速運動してます。
・・・で、等速運動するからどうなんですか??
 AI
AI
重心の運動を見るだけで全体の運動を追いかけることができるんだ。要は運動を単純化できるってこと。
 AKINORI
AKINORI
今回出てきた運動量についてはこちらを確認してください
重心の運動は「全体の運動」を表す

そして先ほど伝えた通り、
「重心の運動」=「全体の運動」です。
式で表した通り、重心は等速度運動をしているんですよ。
ですから、最初に分けた「全体の運動」という部分はただの
等速度運動
だったのです。
これで2体問題の30%は理解できました。
重心がなぜ全体の運動を表すのかを詳しく知りたい人はこちらの記事を見てください。
重心からみた物体の運動を考える=個々の運動を考える

次に「重心から見た物体の運動」を見ていきましょう。
重心から見るというのは、重心から見た物体の相対速度を考えるということです。
それぞれの相対速度はこうなります。
Aについて・・・\(\vec{v_A} = \vec{v_1} – \vec{v_G}\)
Bについて・・・\(\vec{v_B} = \vec{v_2} – \vec{v_G}\)
そして、重心からみた二つの運動量の和を考えてみます。
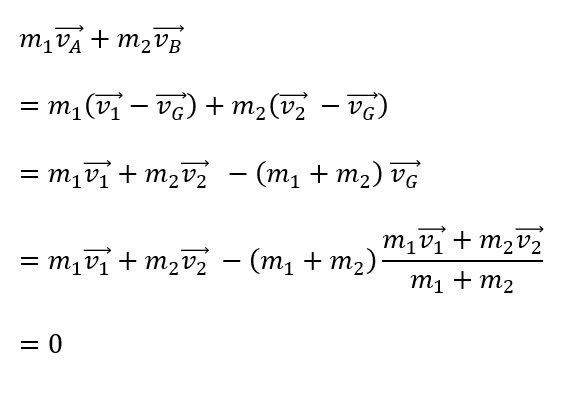
式変形が長くなっちゃいましたが、最終的に言いのは次の式です。
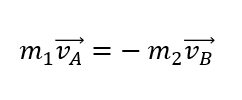
これが個々の運動の性質を表しています。
\(m_1, m_2\)はありますが、大雑把に言えば
左辺は重心から見たAの速度、
右辺は重心から見たBの速度
になっています。
それがマイナスで繋がっているわけです。
つまり、
Aが左向きに動いたら、Bは右向きに動き
Aが右向きに動いたら、Bは左向きに動く
というように、対照的な運動をするのです。
「AとBは重心から見たら、それぞれ対称に単振動している」
ということがここから読み取れるのです!!
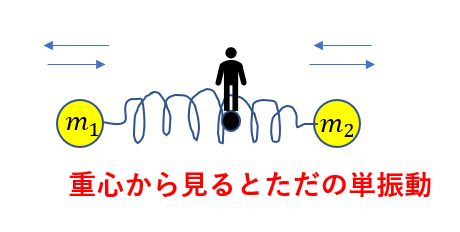
これが個々の運動の正体です。
まとめると
重心を見ると、全体の運動が分かる→等速度運動
重心から物体を見ると、個々の運動が分かる→単振動
このように複雑そうな運動を単純な2つの運動に分解することができるのです。
これで二体問題の60%は理解できました。
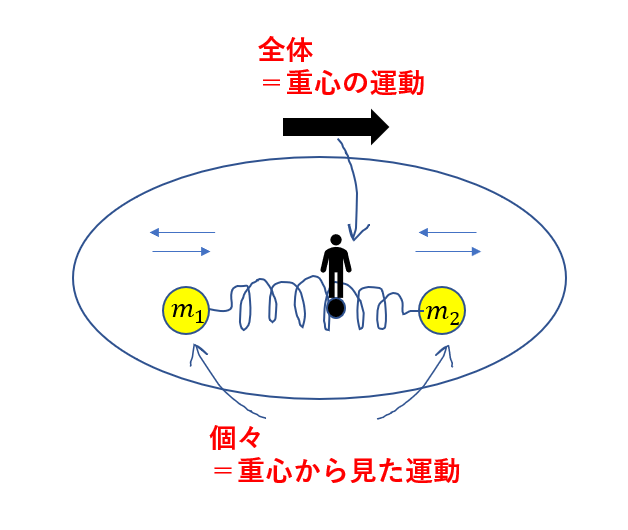
*相対速度についてはこちらを確認してください
重心から見たエネルギー保存則

ここまでは理解できたでしょうか?最後にエネルギーに関してお話をしたいと思います。
二体問題ではエネルギー保存則が重要になってきます。
ほとんどの場合、今回のようなばねを使ったりなど、非保存力が仕事をしない場合が多いです。
つまり、エネルギー保存則の使い勝手がいいんですね。
ここまで、「重心の速度」や「重心からみた物体の相対速度」を考えてきました。
なので、エネルギーに関しても重心の速度や相対速度を使って表していけば良さそうですね。
その書き換えをここで教えていきます。
結論から言うとこうなります。
(力学的エネルギー)
=(重心の運動エネルギー)+(内部エネルギー)
*内部エネルギーは
(重心から見た運動エネルギー)+(ばねの弾性エネルギー)
では詳しく見ていきましょう。
重心系の力学的エネルギー

図の状態でばねの伸びが\(x\)だとしましょう。
ここで、力学的エネルギーを考えてみます。
まず、今回の力学的エネルギーはこの物体をすべて一つの物体と見ているので、
エネルギーをすべて足したものがこの系の力学的エネルギーになります。
AとBの運動エネルギーとばねの弾性エネルギーを足せばいいですね。
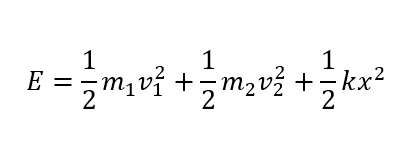
運動エネルギーを「重心」と「重心から見た」エネルギーに変える

ここで、運動エネルギーの部分に注目してみます。
このままだと\(v_1, v_2\)のままで扱いにくいです。「重心速度」と「重心から見た物体の相対速度」を考えてきたので、この部分もうまくそれらに置き換えましょう。
重心から見た相対速度\(\vec{v_A}, \vec{v_B}\)を用いて
\(\vec{v_1} = \vec{v_G} + \vec{v_A}\)
\(\vec{v_2} = \vec{v_G} + \vec{v_B}\)
と表すことができます。
これは「速度」の式です。運動エネルギーには「速さ」を使うので、速さの関係に直します。と言ってもベクトル記号を外すだけです。
\(v_1 = v_G + v_A\)
\(v_2 = v_G + v_B\)
当サイトでは、「速度」と「速さ」を区別するためにベクトル記号を使っています。\(\vec{v}\)は「速度」ですが、\(v\)は「速さ」を表します。
これを運動エネルギーの和の式に代入します。
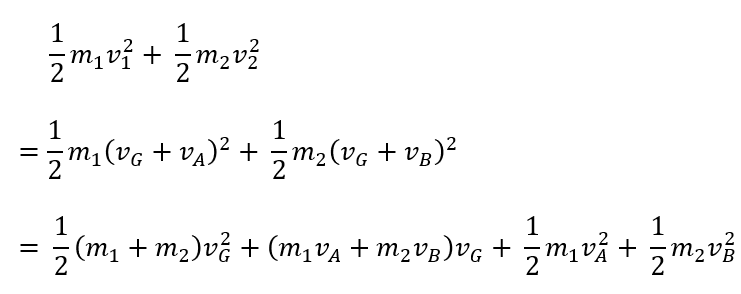
さて、この最後の式を見てみましょう。
まず\(m_1v_A + m_2v_B\)
というのが二項目にありますね。
これは「重心から見た物体の運動」を考えたときに0だと説明しましたね。
なので、二項目は消えます。
そして、残ったものを見てください!
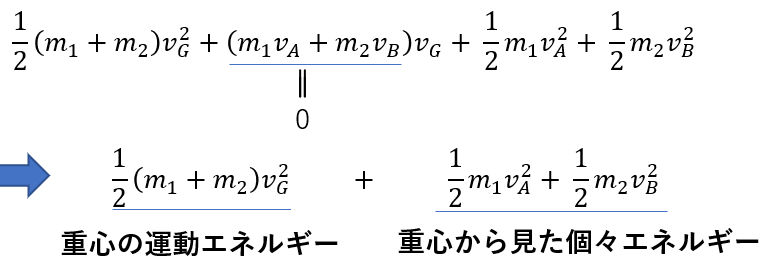
「重心の運動エネルギー」+「重心から見た物体の運動エネルギー」

このようになります。
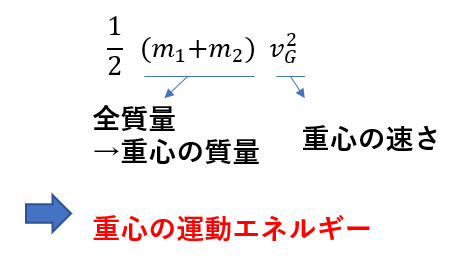
第一項目は\(m_1 + m_2\)という重心の質量(全物体の質量)と重心の速さ\(v_G\)が表れています。
つまり重心の運動エネルギーになっています。
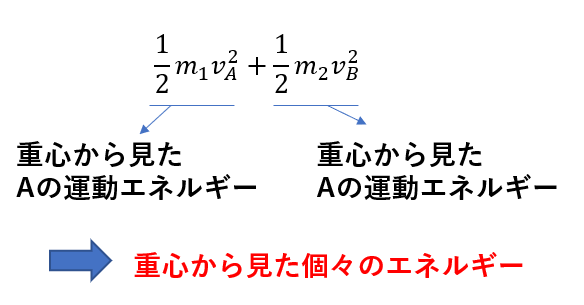
次の第二項目では、\(v_A, v_B\)という風に
重心から見た相対速さ
が表れています
その運動エネルギーの形になっているから、「重心からみた個々の運動エネルギー」とみなせるわけです。
重心系の力学的エネルギー保存則

運動エネルギーの部分を踏まえてもう一度力学的エネルギー\(E\)を見てみましょう。
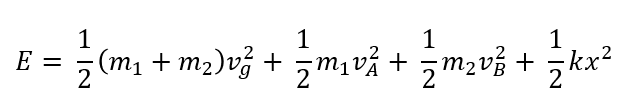
これはこのように解釈できます。
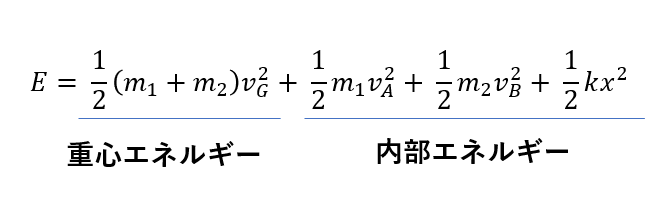
まず一項目の
\(\frac{1}{2}(m_1 + m_2)v_G^2\)
これは言うまでもなく、重心のエネルギーです。
また、重心の運動は「全体の運動」とリンクしていましたね。
つまり、重心のエネルギーは「全体のエネルギー」とも言えるわけです。
一方その他の項は
(重心から見た個々の運動エネルギー)+(弾性エネルギー)
となっていますね。
これを内部エネルギーと呼びましょう(一般的な呼び方ではありません)。
この内部エネルギーは「重心から見たエネルギー」です。
「重心から見た運動」は「個々の運動」というのを先ほど解説してきたわけですから「個々のエネルギー」とも言えるわけです。
つまり、エネルギーに関しても「重心のエネルギー」と「重心から見たエネルギー」に分けることができるのです。
力学的エネルギーは一定になる!

そして、今回もそうですが、二体問題では基本的に非保存力は仕事をしません。
つまり
(力学的エネルギー)=一定
となります。
ですから、最初の力学的エネルギーを求めることさえできれば、この式はものすごい力を発揮します。
このように、二体問題は「重心の運動」と「重心から見た運動」に分けることで単純化します。
それが、エネルギーであってもです。
ここまで読んだあなたは二体問題の90%が理解できています!
・・・残りの10%?
それは問題演習をする部分です!やりましょう!!
まとめ:二体問題は重心を使って「全体」と「個々」に分けろ!

いかがでしたか?
この内容を知っているかどうかで入試問題のレベルがかなり変わってきます。
これを知らないと、全く手を付けられず不合格というのも十分にあり得えます。
難しい内容ではありますが、しっかり内容を理解してください。
二体問題攻略法
→重心を使って「全体」と「個々」に分ける!
重心の運動→全体の運動→等速度運動
重心から見た物体の運動→個々の運動→単振動
重心を使ったエネルギー保存則
(力学的エネルギー)
=(重心の運動エネルギー)+(内部エネルギー)
*(内部エネルギー)=(重心から見た運動エネルギー)+(ばねの弾性エネルギー)
[/topic]








