重心の位置を運動量から求めると面白いことが分かった件
ちょっと今回はですね。重心をもっと理解しようというテーマでやっていこうと思います。
重心って普通モーメントを使って求めますよね?
ですが、それだとどうしても重心の本当の意味を理解できない場合が出てくるんです。
そこで、今回はより本質的に理解するために
モーメントを使わない方法で重心を求めてみたいと思います。
運動量の定義から導く
その方法は運動量から考える方法です。
運動量の定義はこうでした。
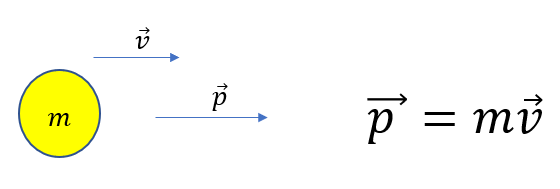
ベクトルの式だったんですよね。
今回は「質量×速度」という形を頭に入れておいてください!
さて、
重心は複数の物体がないと考えてもしょうがないのでこんな状況を考えて見ましょう。
質量\(m_1, m_2\)の物体A,Bが軽いばねでつなげられている。A,Bが位置が\(\vec{x_1} = (x_1), \vec{x_2} = (x_2)\)のとき、速度がそれぞれ\(\vec{v_1} , \vec{v_2}\)であるとする。
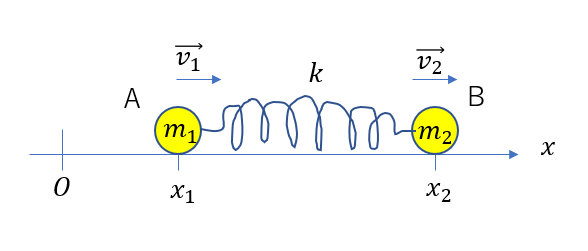
この物体の重心を求めてみます。
運動量を考えるんですが、全体で見るために、運動量を足していきます。
\(\vec{P} = m_1\vec{v_1} + m_2\vec{v_2}\)
重心の意味を考える
ここで、重心について考えておきましょう。
そもそもなんで、重心というの考えるのか?
というと、この物体の運動ってイメージしにくいですよね。
全体は右に動くけど、物体はばねによって振動する。
イモムシみたいな運動で気持ちが悪いですよね。
そこで、全体の運動を考えるために、導入するのが「重心」なわけです。
「もし、重心が全体の運動を代表できるのであれば・・・」
という思いから、重心という概念が出てきたわけですね。
全体の運動を代表するにはいくつか条件があります。
- 全部の質量を持つこと
- 剛体ではなく、質点であること
この二つです。
ということで、これを重心と定めましょう
ということなのです。
それを踏まえてもう一度運動量を考えてみましょう。
\(\vec{P} = m_1\vec{v_1} + m_2\vec{v_2}\)
この運動量\(\vec{P}\)は「全体の運動量」ですから、
当然、重心の運動量はこれと一致していないとだめですよね。
重心は代表点なんですから。
そう考えると右辺はまさに「質量×速度」としてあげたいんです。
ただし、重心は「全質量」を持つので、「質量×速度」のうち「質量」は「全質量」となるべきです。

ということで、右辺を無理やり式変形したいと思います。
\(\vec{P} = m_1\vec{v_1} + m_2\vec{v_2}\)
\( = (m_1 + m_2) ・\frac{m_1\vec{v_1} + m_2\vec{v_2}}{m_1 + m_2}\)
こうすると、「重心の質量×重心の速度」
という形になっているのがわかりますね。

ということで、この
\(\frac{m_1\vec{v_1} + m_2\vec{v_2}}{m_1 + m_2}\)
というのを「重心の速度」と定義してあげようというのです。
重心の速度
\(\vec{v_G} = \frac{m_1\vec{v_1} + m_2\vec{v_2}}{m_1 + m_2}\)
そして、速度についてこのように書けるってことは、位置についても同じように書けるでしょう。
(実際、速度を積分したら位置になるので、両辺積分したら位置の式が出てきますよね。)
重心の位置
\(\vec{x_G} = \frac{m_1\vec{x_1} + m_2\vec{x_2}}{m_1 + m_2}\)
*成分を代入すれば
\(x_G = \frac{m_1x_1 + m_2x_2}{m_1 + m_2}\)
ということで、無事、モーメントから導いたものと同じ結果が得られました。
運動量で考えるとより、「重心が全体の運動を代表する点」という認識できるでしょう。
この理解は非常に重要です!
いかがでしたか?
息抜きにしてはちょっと難しかったですかね?
こういう話も「なるほど!」ってなってくれるあなたは十分物理の力がついていますよ!!









