ばねの弾性力の公式と求め方【向きを含め-kxです】

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
今回は弾性力です。
弾性力といえば\(F = kx\)と知っているかと思います。
しかし、実はこれは間違いです。
弾性力の本当の式を知っていると、単振動でなぜ運動方程式を立てるときにマイナスがつく理由が分かるがわかります。
ばねの弾性力の本当の式が分かる
ばねの弾性力エネルギーの求め方が分かる
目次
ばねの弾性力とは?
ばねは伸びたり縮んだりしますが、ばねには戻ろうとする働きがあります。

ばねが伸びたら縮む向きに、ばねが縮んだら伸びる向きに力がはたらきます。
ばねの弾性力の公式1:フックの法則
ばねの弾性力にはフックの法則というものが成り立ちます。
教科書にはフックの法則についてこう書いてあります。
ばねの弾性力の大きさ\(F\)は、ばねの伸び(縮み)\(x\)[m]に比例する。(フックの法則)
\(F = kx\) (\(k\)[N/m]:ばね定数)
ほとんどの高校生は知っていると思います。
しかし、このフックの法則には大きな落とし穴があります。
フックの法則の説明には「弾性力の大きさ」とありますよね。
実は、フックの法則はあくまで弾性力の大きさについての法則であり、これが受験生を苦しめるんです。
弾性力は「力」、つまりベクトルですから向きも考える必要があります。
プラスマイナスの考慮が必要です。
これが単振動などで苦しむポイントとなります。
ばねの弾性力の公式2:本当は-kxです!
なぜ苦しむかと言うと
運動方程式を立てられなくなるからです!!
大問題ですね。
よくある単振動で「運動方程式が\(-kx\)と、なぜかマイナスがつく問題」の原因となります。
なので、ここで弾性力の真の公式を改めてほしいなと思います。
結論から言いますと次のように書けます。
\(\vec{F} = -k\vec{x}\)
ばねの弾性力を成分で表す
ばねの弾性力はベクトルなので、成分表示しないといけませんね。
成分表示とは以下のようなルールに従って表します。
\(\vec{F} = (大きさ)\)と書く
このとき、軸に対して
- 同じ向き→()の中は正
- 軸と逆向き→()の中は負
これに従って式にしていきます。
弾性力はちょっとくせ者で、ばねの状態によって向きが変わってしまいます。
なので、ばねが伸びている場合と縮んでいる場合で分けて考える必要があります。
では、それぞれの場合で弾性力を成分表示してみましょう。
ばねが伸びている場合
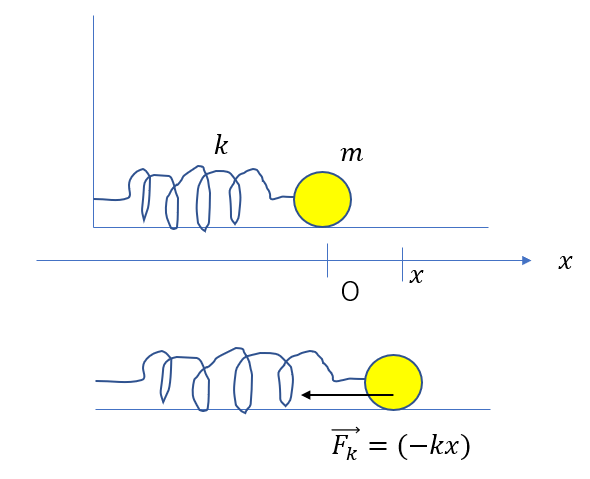
物体がある位置座標\(x\)にあるとき、弾性力を考えてみます。
軸を取るときに原点をばねの自然長に取っておくと\(x\)がそのままばねの伸び(縮み)になるので、原点をばねの自然長に取っておきましょう。
ばねは伸びていて、原点から軸の正の方向にあるので、\(x>0\)となります。
そして、弾性力の成分を求めるために大きさをまず求めます。
これはフックの法則より\(kx\)です。
そして、次に向きを考えます。
ばねが伸びている場合は左向きに、つまり軸と逆向きにはたらきます。
ですから、先ほどの成分表示の方法に従えば、()の中身は負になります。
\(kx\)は正だったので、成分表示すると
\(\vec{F} = (-kx)\)
となるわけです。
ばねが縮んでいるとき
次はばねが縮んているときです。
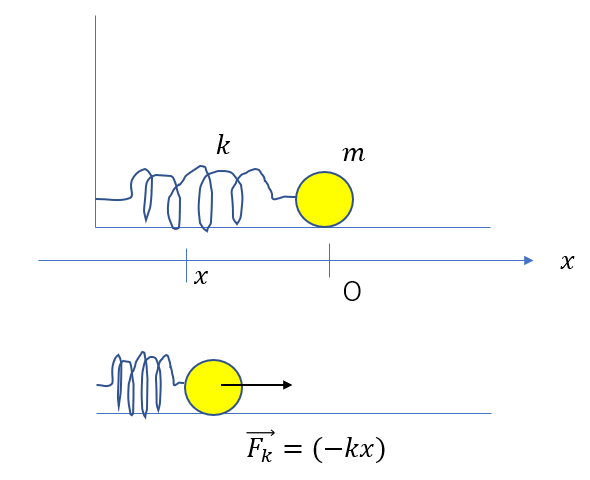
同じように考えます。
ばねが縮むと、原点より左側に来るので、\(x<0\)となります。
成分表示するために、まずは大きさを求めますがこれも同じで
\(kx\)です。
次に向きを考えますが、ばねの弾性力の向きは右向きで軸と同じなので、()の中身は正です。
\(kx < 0\)なので、正にするにはマイナスをつける必要がありますね。
\(\vec{F} = (-kx)\)
このように成分表示できます。
ばねの弾性力の真の公式
場合分けをしましたがよく見たらばねが伸びていようが縮んでいようが
\(\vec{F} = (-kx)\)
と表せています。
なので、弾性力は次のように一般化できます。
\(\vec{F} = (-kx)\)
つまり、マイナスがつく理由はいたってシンプルで、「向きを考えたら自然とマイナスがつきますよね?」という感じです。
単振動をやるまでは弾性力がきても力のつり合いだったり、弾性エネルギーを考えるだけだったので大きさだけでもよく\(F = kx\)でうまくいってました。
ところが、単振動になると運動方程式を立てる必要が出てきます。
運動方程式を立てる際はベクトル(つまり大きさに加えて向きも)を考えないといけません。
なので、急にマイナスが出てきて混乱するわけですね。
ばねの弾性力は\(F = kx\)ではないんです。
ちなみにこの式は成分表示で書いていますが、変位\(\vec{x}\)を使えば
\(\vec{F} = -k\vec{x}\)
とも書けます。
見ての通り弾性力は「ばねの伸び(縮み)の距離」ではなく、変位を使う必要があるんですね。
ばねの弾性エネルギーの求め方
ばねの弾性力の話が出てきたので、ばねの弾性エネルギーについても紹介しておきます。
これは仕事とエネルギーの概念を理解しておく必要があるので、こちらの記事をご覧ください。こちらで導出含め、分かりやすく解説しています。
まとめ:ばねの弾性力の真の公式
いかがでしたか?
ばねの弾性力の本当の公式が分かると単振動がスムーズに理解できます。
しっかり復習して理解しておきましょう!
ばねの弾性力の真の形
\(\vec{F_k} = -k\vec{x}=(-kx)\)
(\(\vec{x}\)は変位)
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!








