円運動の公式の覚え方と運動方程式・エネルギー保存則の使い方

どうも!オンライン物理塾長あっきーです!月3万回見られるサイトを運営し、オンライン塾も運営してます!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
あっきーさん。円運動の問題が解けなくて・・・解き方のコツはありませんか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
今回はこのような悩みを解決します。
結論から言うと、円運動の問題は以下の2点に注目すれば問題が解けます。
- 運動方程式
- エネルギー保存則
円運動ならではの公式も確認しつつ、この2式を使いこなすことで円運動の問題はヌルゲー化します。
アッと驚く解法を見ていきましょう!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
目次
円運動とは
円運動とはまさに「円軌道をする物体の運動」です。
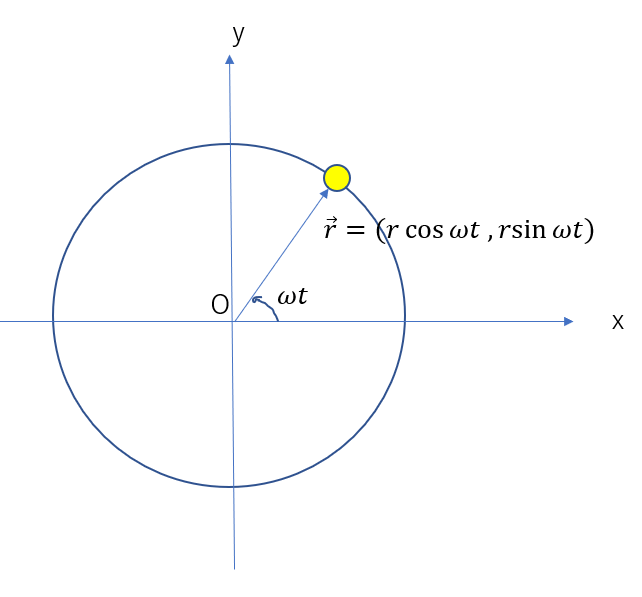
円運動の公式
円運動では位置や速度を考えるときに「角度」を考えると非常に単純化できます。
図のように角度が分かっていればsinとcosを使って物体の運動を考えることができるからです。
そこで、「一秒間にどれだけ角度が変化するか」という意味の角速度を導入しましょう。
- 角速度\(\omega\)
つまり、「一秒間で角度\(\omega\)だけ移動する」ということです。
じゃあ、\(t\)秒間では?というともちろん\(\omega t\)だけ移動します。
これを用いることで、物体の位置、速度、加速度を求めることができます。
ただ、円運動では見ての通りx,yの二つの軸を取っていますね。このサイトでは1つの軸についてしか扱っていないので、嫌です(笑)
なので、円運動ではちょっと裏技を使います。
先に向きを定めて、あとは大きさだけを考える!!
向きに共通ルールを決めちゃって、大きさだけ考えるようにしよう。
ってことです。
速度、加速度の向きと大きさについてはこうなります。
等速円運動の場合
速度 : \(v = \omega r\)(反時計回りに正)
加速度:\(a = \omega^2 r = \frac{v^2}{r}\) (中心向きを正)
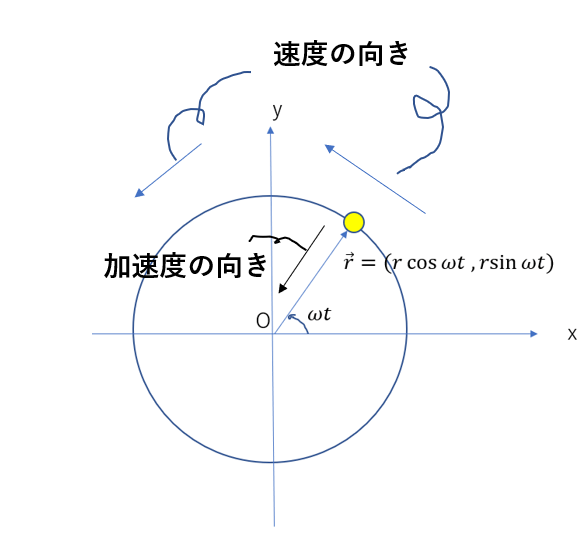
公式の覚え方
この公式の覚え方ですが、半径に\(\omega\)を掛けていくイメージで覚えると良いです。
\(\omega\)を一回ずつかけていくと
半径→速度→加速度
となっていくのがわかりますね。

等速円運動でも加速度は生じる
高校物理では円運動の中でも「等速円運動」を扱うことが多いです。
しかし、等速の場合でも加速度が生じます。
その理由は、加速度の意味をもう一度振り返ると分かります。
加速度とは「速度の変化」のことです。
「速度」です。速度はベクトルなので、向きも含めて「速度」なんですね。
つまり、大きさ(速さ)が変わっていなくても、向きが変わっていれば速度は変化してるのです。
等速円運動では、向きはちゃんと変わっていますね。だから加速度が生じています。
円運動で問題の解き方
円運動の速度、加速度を学んだところで、円運動の解き方を教えていきます。
円運動の問題が出てきたときは真っ先にこの二つを思い浮かべてください。
・運動方程式
・エネルギー保存則
この2つを利用することで円運動の問題は簡単に解けます。
また、これらの使い方も基本1つしかないので、円運動の問題は単純化します。
円運動の運動方程式
まずは運動方程式。
円運動であろうと、運動方程式の立て方はこの手順でやっていきます。

ただ、今回注目したいのはStep 2です。
軸の取り方です。
軸は加速度の方向に合わせて取ります。
今回の加速度はの向きは円の中心向きですよね。
なので、軸も当然「円の中心方向」について考えないといけません。
円運動の場合は加速度が必ず中心向きなので軸は絶対に中心向きを正として取りましょう!!
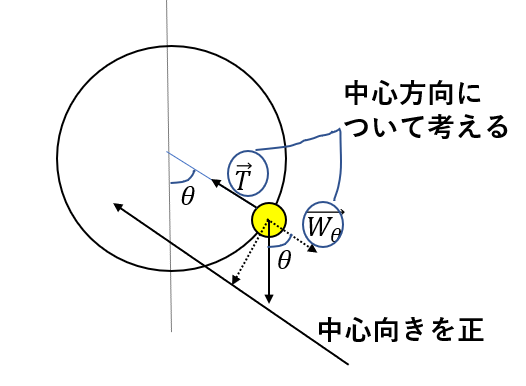
もう一つ注目すべきなのはStep 5です。
中心方向の運動方程式を立てるときは、加速度が具体的に代入できますね?
円運動の加速度の大きさはこうかけるんでしたね。
\(a = \omega^2 r = \frac{v^2}{r}\)
これを代入することを忘れないでくださいね。
あと、加速度は\(\omega\)と使う場合と\(v\)を使う場合、の両方を使います。
問題文で与えられている方の物理量を使わないといけないので、式変形できるようにしておいてね。
円運動のエネルギー保存則
次に、エネルギー保存則です。
円運動は
エネルギー保存則とめちゃめちゃ相性がいいんです。
エネルギー保存則というのはこういうこういうものです。
(はじめの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
例えば、糸の張力による円運動を考えてみましょう。
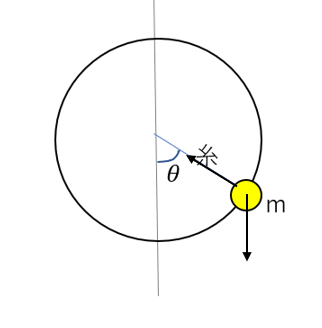
この物体には「重力」と「糸の張力」の二つの力が働いているわけですが、このうち重力は保存力です。
なので、非保存力にされる仕事は張力の仕事だけを考えれば良いんですね。
さて、張力は円の中心向きに働いているわけです。一方、物体はどう動くでしょうか?
一瞬一瞬でみたら、円の接線方向です。
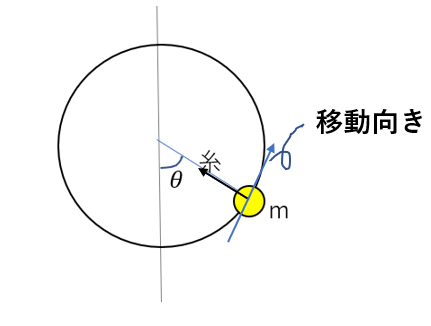
あれ?この二つって垂直じゃない??
力と移動向きが垂直ならば、仕事はゼロです。
ってことで、張力のする仕事はゼロということが分かりました。
・・・
もうお気づきですね。
(非保存力にされた仕事)=0
ということです。
円運動では必ず、中心向きの力が働き続けないといけないわけですがこの力は仕事をしないわけです。
ですから、円運動ではエネルギー保存則がめちゃめちゃ相性がいいのです
ということで
- 運動方程式
- エネルギー保存則
これらをまず思い浮かべれば、ほぼ間違いなく解けます。
円運動でよく問われる問題
とはいえ、運動方程式やエネルギー保存則を適用しても、そこから解くべきことが問われます。
例えば、円運動でよくあるのが「1周する条件」です。
運動方程式とエネルギー保存則を使うのが基本でそのあとに状況をイメージして求めたいものを求める力は必要です。
以下の記事で1周する条件について解説しているのでぜひ読んでくださいね!
まとめ:円運動は運動方程式とエネルギー保存則
いかがでしたか?
円運動は力学の中でも簡単な単元です。
ですから、円運動は満点を取りに行くようにした方が良いですね。
ぜひ、今回学んだことを意識して問題演習をしてください!
- 等速円運動の物理量
速度:\(v = \omega r\) (反時計回りを正)
加速度:\(a = \omega^2 r = \frac{v^2}{r}\)(中心向きを正)
- 円運動のアプローチ法2つ
・運動方程式(中心方向について)
・エネルギー保存則((非保存力にされた仕事)=0となる!)
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!










