単振動の運動方程式の立て方と問題解法を分かりやすく解説します

どうも!オンライン物理塾長あっきーです。現役で早稲田大学に合格し、月2万人が利用するオンライン塾サイトを運営しています!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
単振動の運動方程式を立てるのが全然できないんです。加速度でマイナスがついたり、エネルギー保存則の立て方が理解できないです。
 リケジョ志望のAIさん
リケジョ志望のAIさん
今回はこのような悩みを解決します。
結論から言うと
・マイナスがつく理由→運動方程式を立てる手順に従う
・エネルギー保存則→ばねの置き換え
です。
僕は単振動でやるべきことが1通りしかないことを見つけ出しました。
入試で絶対に間違えない単振動について詳しく見ていきましょう!
単振動とは?
単振動は円運動と関連付けて考えてもらうとよくわかります。
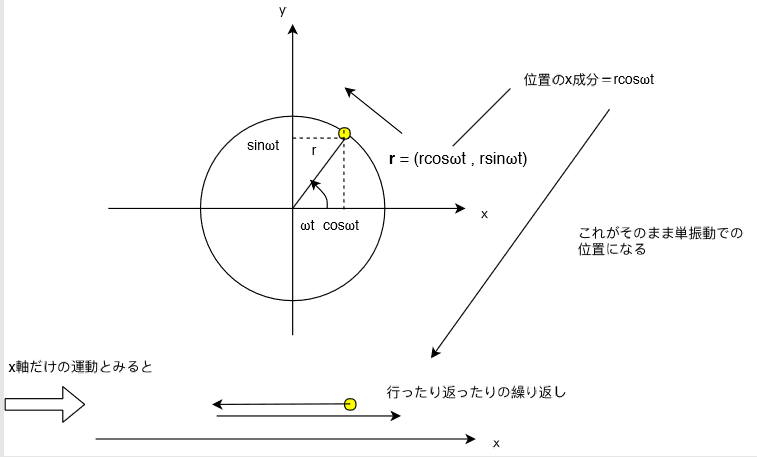
円運動をx軸だけ見てみるとどんな運動になると思いますか?
図のように、右に行っては左に行って・・・
という感じでまさに振動しますよね。
これが単振動です。
もちろん、y軸だけ見ても同じように振動することが分かりますね。
このように、円運動のをどちらか一方の軸だけで見たときが単振動ということです。
単振動の位置、速度、加速度
単振動で出てくる物理量についていて簡単に学びましゅう。
円運動をx軸で見たときの単振動を考えます。
半径\(r\)で角速度\(\omega\)の円運動をする物体の位置について、x成分、y成分を考えるとこうなります。
\(x = r\cos{\omega t}\)
\(y = r\sin{\omega t}\)
そして、このxだけを考えたものが単振動だったので、単振動の位置は
\(x = r\cos{\omega t}\)
となりますね。
この\(r\)は円運動の半径ですが、単振動では「振動の端の位置」、つまり振幅\(A\)を使って置き換えます。分かりやすいです。
単振動は一直線の運動なので、ベクトルで表示しておきましょう。
\(\vec{x}= (A\cos{\omega t})\)
同じように、速度と加速度も円運動の速度のx成分、y成分を考えれば良いのですが面倒ですね。
そこで次の関係を使います。
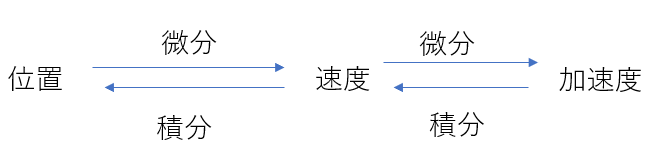
さっき求めた位置を使って微分しまくれば速度と加速度が出ます。
これは数Ⅲを習っている人ならできる(理系ならだいたい習っていると思います)と思うのであまり詳しくは説明しません。
位置を\(t\)で微分すると
\(\vec{v} = (-A\omega \sin{\omega t})\)
さらに\(t\)で微分すると
\(\vec{a} = (-A\omega ^2 \cos{\omega t})\)
\( = -\omega^2 \vec{x}\)
このように単振動の位置、速度、加速度を表すことができました。
この中でも特に注意してほしいのは以下の2式です。
速さの最大:\(v_M = A\omega \) (振動の中心で最大)
加速度の式:\(\vec{a} = -\omega^2 \vec{x}\)(xは位置座標)
まず、速さの最大が\(v_M = A\omega\)とかけるということです。
速度の式を見ればsinが含まれていますね。プラスマイナスを無視すればsinの最大は1です。
なので速さの最大は\(v_M = A\omega\)となります。
たまに聞かれることがあるので覚えておくと良いでしょう。
そして、もう一つ。
\(\vec{a} = -\omega^2 \vec{x}\)
です。
これは単振動の運動方程式を立てる際に非常に重要になるので、覚えておきましょう。
sinとcosの違いは?
先ほど\(x\)の式をcosの形にして書きましたがsinの式で書いても問題ありません。
sinとcosの違いは、最初の位置がどこにあるかという違いです。
sinの場合\(t=0\)では\(x = 0\)となるので原点からスタートするということです。
cosの場合\(t=0\)では\(x=A\)となるので、振動のは時からスタートするということになります。
単振動の運動方程式の立て方
では、単振動の運動方程式を考えていきましょう!
図のように、ばね定数\(k\)に質量\(m\)の物体をつける。ばねの端は壁に固定されている。物体にはばねの力のみはたらくとし、物体は水平方向のみの運動をする。この物体に運動方程式を立てて、この運動について考えよ。
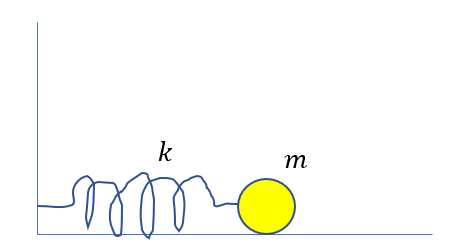
運動方程式を立てるときはステップがありましたね。

等加速度運動だろうと円運動だろうと単振動だろうと「運動方程式を立てる」と言われたら例外なくこの手順で立てます。
運動方程式についてはコチラをチェックしてください。
単振動の運動方程式の立て方1:物体を決める
これはもちろん物体です。
単振動の運動方程式の立て方2:軸を取る
軸は加速度方向に取るのが普通です。
今回は水平の運動なので水平方向に軸を取ります。左右の向きはどちらでもOKです。
ただ、今回は原点も決めておきます。
これは鉄則があって、原点は必ずバネの自然長の位置に取ります。
たまにつり合いの位置に取る場合もありますが、ばねの自然長の位置に取った方が分かりやすいです。
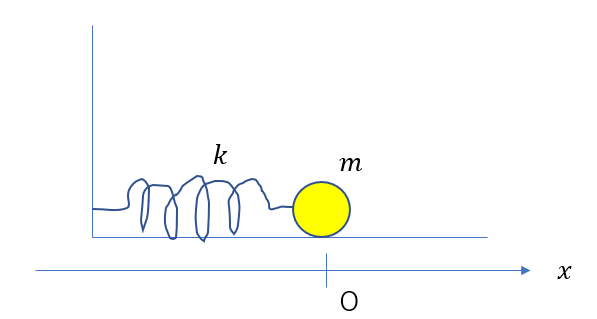
単振動の運動方程式の立て方3:力をベクトルで書く
次に物体に働く力を見ていきます。ここが超重要です。
今回はたらく力はばねの弾性力のみですね。これを成分表示していきましょう。
ばねの弾性力はちょっとくせ者で、状況によって力の向きが違うんですね。
縮んでいるときと伸びている場合で働く向きが逆なんです。
なので、それを考慮しないといけないわけです。
ということで、ばねが縮んでいるときと伸びているときで場合分けしましょう。
ばねが伸びているとき
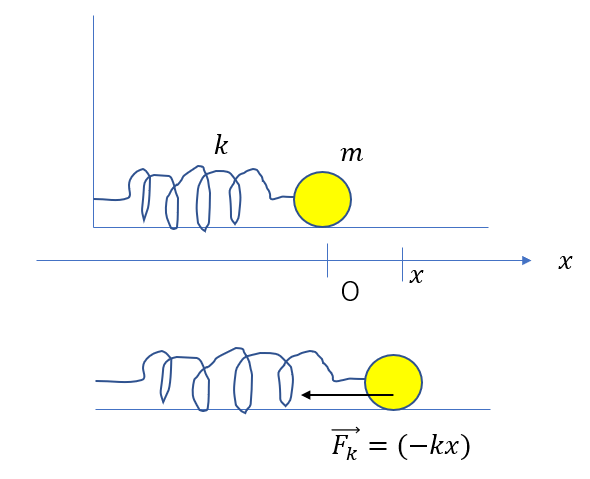
ばねが伸びているとき、つまり原点より物体が右(正)にあるときです。
このとき、物体の位置xは正です。\(x > 0\)
ここで、原点をバネの自然長の位置に取ったのを思い出してください。
なぜこの位置に取ったのかというと、バネの伸び(縮み)が原点からの位置と同じになるからです。
今回の場合\(x\)がそのままバネの伸びとなるのです。
なので、ばねの弾性力の大きさは\(kx\)です。そして、向きは左向きです。
軸と逆向きということは、バネの弾性力を\(\vec{F_k} = (〇)\)と表そうとするとき、この成分(〇ところ)は負になっていないといけないわけですね。
\(k , x > 0\)でしたから、成分を負にするにはマイナスをつけないといけませんね。
ということで、ばねの弾性力を表すと・・・
\(\vec{F_k} = (-kx)\)
となります。
- ばねが縮んだ時
同じようにばねが縮んだ場合も考えましょう。
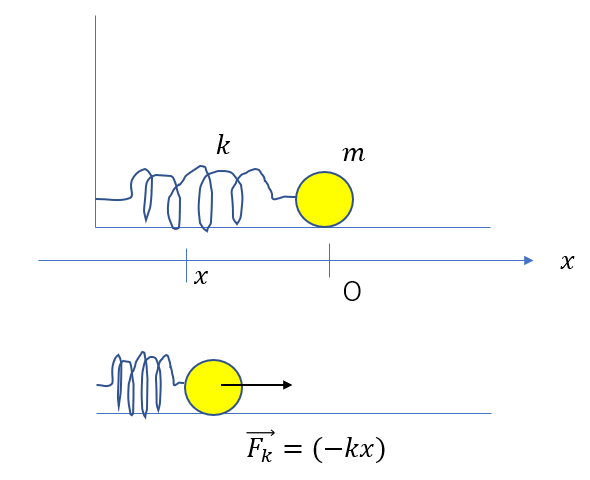
ばねが縮むということは、今回の物体の位置成分\(x\)は\(x<0\)です。
そして、ばねの働く向きは右向きなので、成分は正になる必要があります。
\(kx < 0\)ということを考えれば、ばねの弾性力の成分が正になるにはマイナスをかける必要がありますね。
\(\vec{F_k} = (-kx)\)
二通りの場合を考えましたが、よく見ればどっちの場合も
\(\vec{F_k} = (-kx)\)
と書けていることが分かりますね。
となので、いちいち場合分けしなくても一般的にバネの弾性力は
\(\vec{F_k} = (-kx)\)
と表せます。
単振動の運動方程式で\(-kx\)とマイナスがつく理由もこのように一つ一つ運動方程式を立てていけば簡単に分かるのです。
単振動の運動方程式の立て方4:合力を求める
ばねの弾性力のみ働くので、弾性力がそのまま合力になります。
\(\vec{F} = \vec{F_k} = (-kx)\)
単振動の運動方程式の立て方5:運動方程式を適用
後は運動方程式\(m\vec{a} = \vec{F}\)に今までの成分を代入していきます。
\(\vec{a}\)を求めたいのでここは単純に\(\vec{a}=(a)\)として代入します。
\(ma = -kx\)
これで運動方程式を立てることができました。
単振動が起こる条件
この運動方程式をもう少し変形します。
\(a = -\frac{k}{m}x\)
これはこんな形をしています。
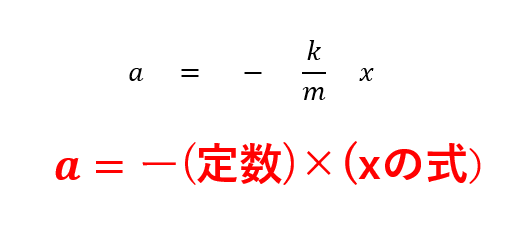
実は、加速度がこのような形で書けるとき、物体は単振動するということが分かっています。
単振動が起こる条件
\(a = – (定数)×(xの1次式)\)
運動方程式を立ててたまたまこういう式になったので「あ!単振動するんだな」という感覚を身に付けて欲しいです。
単振動の問題を解くときにやるべき3つのこと
ここから問題の解法についてお話をします。
運動方程式を立てて、単振動の条件式が導けた後、絶対にやってほしいステップが3つあります。
- 振動の中心\(x_0\)を求める → \(a = 0\)のときの位置
- \(a = -\omega^2 (x – x_0)\)とし、\(\omega\)を求める→ \(\omega = \sqrt{定数}\)
- 周期\(T\)を求める→\(T = \frac{2\pi}{\omega}\)
単振動の問題解法1:振動の中心を求める
まず、振動の中心を求めます。振動の中心は\(a=0\)として求めることができます。
今回の水平バネの場合
\(a = -\frac{k}{m}x\)
に\(a = 0\)を代入すると
\(x_0 = 0\)
となります。中心は原点ということが分かりますね。
単振動の問題解法2:角振動数\(\omega\)を求める
次に単振動の角振動数\(\omega\)を求めます。
最初に単振動するときの加速度の式を教えました。
\(\vec{a} = -\omega^2\vec{x}\)
これと先ほどの式で比較をします。
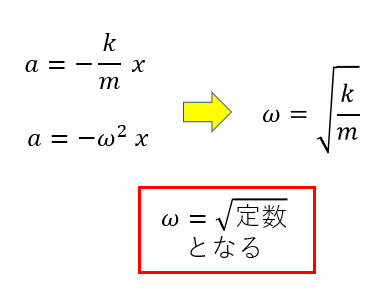
このように\(\omega = \sqrt{定数}\)と書くことができます。
今回の場合で言えば
\(\omega = \sqrt{\frac{k}{m}}\)
です。
ただ、いちいち代入して求めるのは面倒なので、\(\omega\)はダイレクトに求めても良いです。
\(a = – (定数)×(xの式)\)
の式の定数の部分が\(\omega^2\)になるので
\(\omega = \sqrt{定数}\)
と表せます。
単振動の問題解法3:周期\(T\)を求める
最後に単振動の周期(往復時間)を求めます。
これは
\(T = \frac{2\pi}{\omega}\)
と表せます。なので今回の場合
\(T = 2\pi \sqrt{\frac{m}{k}}\)
となりますね。
単振動の問題では、どんな問題であれ、この3ステップを踏んでほしいと思います。
単振動のエネルギー保存則
単振動ではエネルギー保存則が成立します。
これにはあるテクニックがあります。それは「置き換え」です。
置き換えをやることでミスが激減します。
それをぜひ身に付けてほしいです。
詳しくはこちらをチェックしましょう!
単振動の問題にはどんなものがある?
入試では単振動の問題はいろんなものと絡んできます。
- ばねが2つ
- 浮力による単振動
- 静電気力による単振動
- 摩擦のある単振動
様々ありますが、それぞれをパターン化して解法を暗記するのではなく、ここで学んだことをすべての問題に適用できるように練習してください。
ここで学んだことこそ、単振動のたった1つの解法なのです。
まとめ

いかがでしたか?
ここで学んだことは入試でそのまま使います。
この内容を理解していれば、単振動はぬるいです。
しっかり復習して問題に取り組んでください。今までとは比べ物にならないくらいスラスラ解けるはずです。
・単振動の物理量で重要な式
速さの最大\(v_M = A\omega\)
加速度:\(\vec{a} = -\omega^2 \vec{x}\)
・単振動である条件
\(a = – (定数)×(xの式)\)
・単振動だと分かったらすべきこと
- 振動の中心\(x_0\)を求める → \(a = 0\)のときの位置
- \(a = -\omega^2 (x – x_0)\)とし、\(\omega\)を求める→ \(\omega = \sqrt{定数}\)
- 周期\(T\)を求める→\(T = \frac{2\pi}{\omega}\)
・単振動のエネルギー保存則
→水平バネに置き換えよ!
・合力を求めて\(F=-k(x-x_0)\)の\(k\)にあたる部分を水平バネのばね定数にする
・\(F = -k(x-x_0)\)の\(x_0\)を水平バネの自然長にする。
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!














