知らないとやばい!?浮力による単振動を徹底解説します!

浮力による単振動が理解できる
単振動の問題が楽々解ける
単振動の理解がさらに深まる
こんにちは!
今日は、受験レベルの単振動の問題を解説していきます。
そのテーマは
浮力による単振動です!!
でた~。これいつも分からなくなっちゃうんですよね。
 リケジョになりたいAIさん
リケジョになりたいAIさん
そうだね。単振動ということに気づかない人も多いんだ。
 あっきー
あっきー
単振動=ばねの振動
というように解釈している方も多いんじゃないかな、と思います。
ですが、単振動はばねの場合がほとんどですが、ばねがすべてではありません。
その中でも代表的なのが浮力による単振動なのです。
やることはばねの場合と変わらないのですが、今回は入試レベルの応用問題として浮力による単振動の問題を解説しようと思います。
目次
「単振動=ばね」は間違い

今回の問題に入る前に、こちらで単振動の基礎知識をつけておいてください。
ここにも書いてありますが、単振動になるには条件があります。
それも式で表せる条件です。それが
\(a = – (定数)×(xの一次式)\)
です。
運動方程式を使って計算した結果、このような式の形にできれば単振動だと分かるのです。
「単振動=ばねの振動」ではなく
「単振動=a = – (定数)×(xの一次式)」
と理解しておきましょう。
それを踏まえて浮力による単振動の問題を解きましょう!
 あっきー
あっきー
浮力による単振動
一様な断面積\(S\)、高さ\(h\)の浮きがある。これを水面に浮かべたら図1のように頭を水面上に\(\frac{1}{3}h\)だけ出して静かに静止した。水の密度\(\rho\)、重力加速度の大きさを\(g\)として、浮きの運動に伴う水の抵抗と水面の変化は無視する。
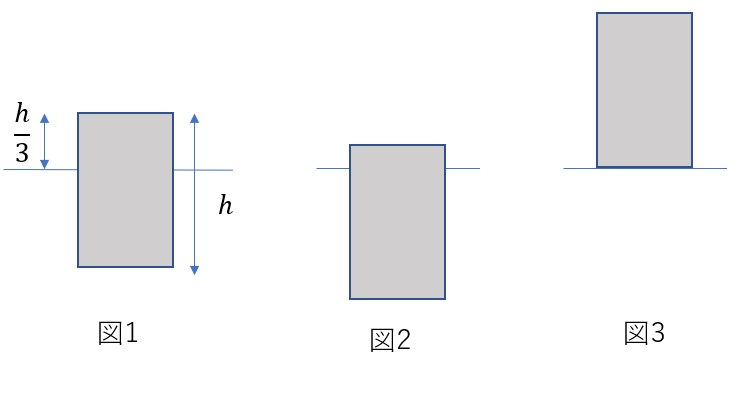
(1) 浮きの質量\(m\)はいくらか。
(2) 浮きをその上面が水中に沈まない程度に鉛直に押し下げ(図2)、手を放すと、浮きは上下に振動を始める。その周期\(T\)はいくらか。
(3) 図3のように、浮きの底面を水面と接するように保ち、手をはなした。浮きが沈んでゆき、ちょうど上面が水面と一致したときの速さはいくらか。
(4) 浮きはさらに沈んでゆくが、最も沈んだとき、その上面の、水面下の深さ\(d\)はいくらか。
「静止する」→力のつり合い

(1)では浮きが静止しているので、力がつり合っているんですね。
今回は図のように、重力と浮力の力が働きます。
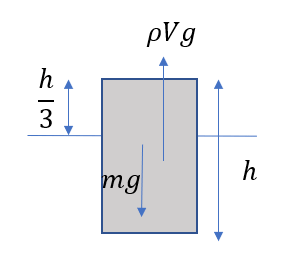
浮力の大きさは
\(F = \rho Vg\)
と表すことができます。
\(\rho\)は流体(今回は水)の密度
\(V\)は物体の流体内にある体積です。
今回の\(V\)は「底面積×高さ」で表せるので
\(V = S\times \frac{2}{3}h\)ですね。
後は力のつり合いを考えればOKです。
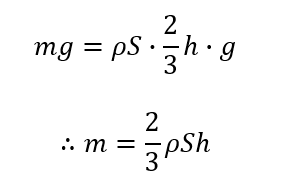
単振動のステップをしっかり行おう

(2)の問題は「振動」、「周期」という言葉があるので単振動するのはイメージつきますが
何にせよ、運動方程式を使ってa = – (定数)×(xの一次式)の形を目指しましょう。
運動方程式の立て方に沿って行きます。
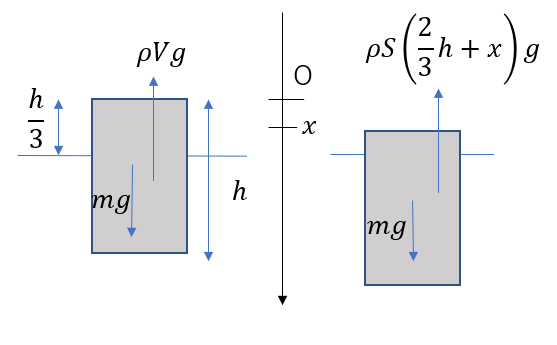
まず、軸を取ります。上向きでも下向きでもどっちでも良いですが、今回は下向きでいきましょう。
また、原点を「つり合いの位置」に取ります(上面の位置で見ていきます)。
そこから、ある位置\(x\)で運動方程式を適用していきます。
力は図のようになって、(1)と同様に、重力と浮力がかかります。
ですが、(1)と異なり水の中にある体積が変化しますね。
最初\(\frac{2}{3}h\)の高さだけ沈んでいましたが、今は位置\(x\)のところを考えていますので
プラスで\(x\)だけ沈みます。
つまり\(\frac{2}{3}h + x\)の高さだけ沈んでいますね。
つまり浮力の大きさはこうなります。
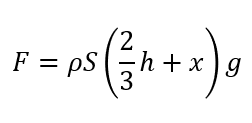
これは大きさなので、運動方程式を立てる際には正負も考慮しないといけません。
軸は下向きですが、浮力は上向きです。
なのでマイナスをつける必要があります。
ということで合力\(\vec{F_s}\)はこう表せますね。
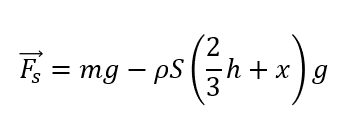
あとは運動方程式を適用すればOKです。
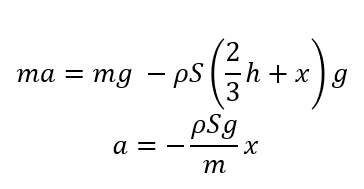
(\(m\)はとりあえず代入せず残しています)
これは\(a = – (定数)×(xの一次式)\)の形になっていますね。
つまり単振動するということが確認できました。
ここまでできたら単振動の章で3つのステップをやれと言いました。
その3ステップをやっていきます。
振動の中心
これは\(a = 0\)となるときの\(x\)でした。
先ほど導いた式から、振動の中心は\(x_0 = 0\)となります。
つまり、最初に設定した原点(力のつり合い位置)が振動の中心となるわけですね。
\(\omega\)を求める
これは\(\omega = \sqrt{定数}\)という関係があったので簡単に求めることができます。
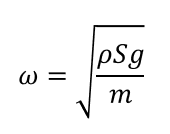
周期\(T\)を求める
このステップがまさに(2)の答えとなりますね。
\(T = \frac{2\pi}{\omega}\)という関係があるのでこれを使って最後に\(m\)に(1)の答えを代入すれば答えがでますね。
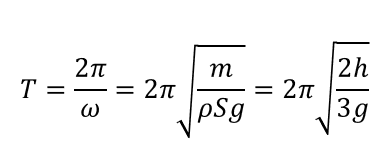
エネルギー保存則を使おう

今回の運動は(2)でも見たように単振動です。
つまり等加速度運動ではないので、等加速度運動の公式は使えません。
単振動の速さの式もあるにはありますが、基本的に使えません。
となれば考えられる方法はただ一つです。
エネルギー保存則です。
エネルギー保存則についてはこちらを確認くださいね。
単振動のエネルギー保存則なんて知らない・・・
 リケジョを目指すAIさん
リケジョを目指すAIさん
そうだね。でも「置き換え」という手法を使えば良いんだ。
 あっきー
あっきー
単振動は\(a = -(定数)×(xの一次式)\)と書くことができるわけです。
もっと言えば\(F = – kx\)の形にできるわけですね。
この形ってどこかで見たことありますよね?
ばねの弾性力と同じ式だ!
 リケジョを目指すAIさん
リケジョを目指すAIさん
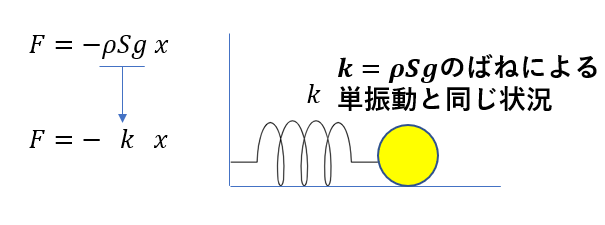
今回の浮力の単振動は、図のようなばね定数をもったばねの単振動と同じなわけです。
そのようにみなせば、エネルギー保存則が使えますよね。
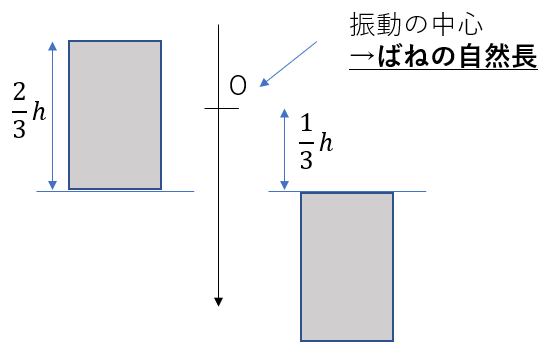
ばねの弾性エネルギーは自然長からの伸びを調べないといけませんのでそこは注意しましょう。
最初は\(\frac{2}{3}h\)伸びていて、最後は\(\frac{1}{3}h\)だけ伸びています。
後はエネルギー保存則を使いましょう。
エネルギー保存則は
(初めの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
でした。
これを当てはめると
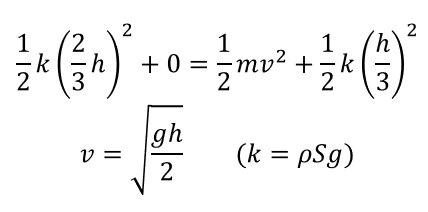
このように答えを出すことができます。
完全に沈んだ場合は等加速度運動

(4)はここまでの状況とは違って浮きがすべて沈んだ状態になっています。
高さ\(h\)の浮きが水中にすべて沈んでいるので、浮力の大きさは
\(F = \rho Shg\)
となります。
同じように運動方程式を立てると
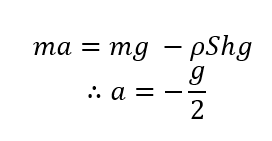
このようになりますね。
今まで単振動でしたが、もはやこれは等加速度運動になっています。
なので、等加速度運動の公式を使えばいいですね。
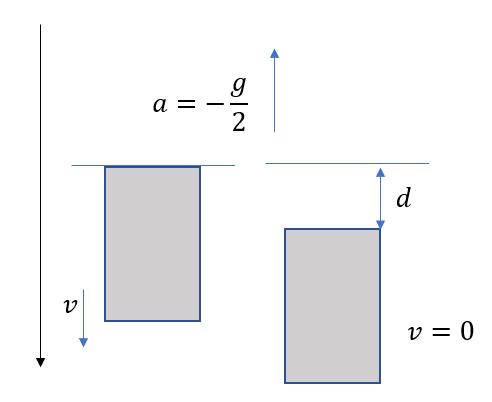
時間の情報が無いので
\(v^2 – v_0^2 = 2ax\)を使いましょう。
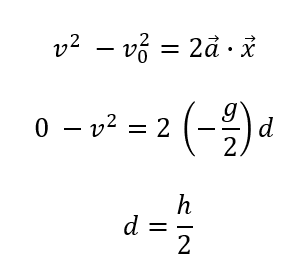
答えが出ましたね。
以上で解説は終わりです。
単振動はやっていることは同じ

いかがでしたか?
浮力の単振動だろうと、ばねが2個あろうと
単振動は単振動です。
やることは全く同じなんです。
運動方程式を立てて、単振動の条件式を導き、3つのステップをクリアする。
これが基本です。たとえ問題に「周期を求めよ」というのが無くても絶対にやってください。
これさえできていれば、後は今回のようなばねに置き換えてエネルギー保存則を立てるなどの応用力を問題を通じて身に付ければあっという間に物理の点数は伸びてきます。
頑張りましょう!!
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!









Comment
この問題の場合、(3)はなぜ単振動の速度の公式が使えないと書いてあるのでしょうか…
私はエネルギー保存則よりも運動方程式で解いた方が
間違えも少なく、簡単だと思いました。
ばね定数に置き換えたところで、定数部分をkと書き換えるなら、k=ρSg/mにならないんですか?
なぜ、分母のmを無視できるんですか?