摩擦のある単振動の問題！やるべきことは一つだけ！！
単振動のところで摩擦のある問題に出くわしたんですが・・・もうさっぱり！
AI
なるほど、ちょっと複雑になった場合だね。でもね、要は単振動なんだよね？だったらやるべきことは？
AKINORI
運動方程式立てて、３ステップやって・・・
AI
そうそう！単振動の問題ならやるべきことは決まっているよね！
AKINORI
今日は応用問題として、「摩擦のある単振動」をやっていきたいと思います。
と「摩擦がある」とか言ってるけど、結局は単振動なわけですよ。
つまり、単振動の解き方
これを知っていれば何のことは無い、超簡単な問題なんです。
ではいきましょう！
単振動についてはこちらをチェック！！
目次
摩擦のある単振動
ばね定数\(k\)の軽いばねの一端に質量\(m\)の小物体をつけ、他端を壁に固定する。ばねが自然の長さになるときの小物体の位置を原点とし、図の右向きに\(x\)軸をとる。床と小物体との間の静止摩擦係数を\(\mu\)、動摩擦係数を\(\mu’\)とする。時刻０において、小物体は、原点を速さ\(v_0\)で\(x\)軸の正の向きに通り過ぎた。重力加速度の大きさを\(g\)とする。
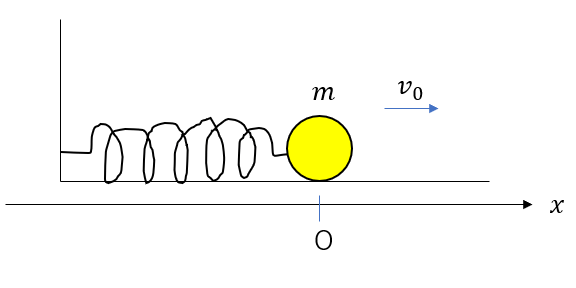
（１）小物体の速度が最初に０となる時刻\(t_1\)での、小物体の位置\(x_1\)を求めよ。
（２）小物体が（１）の位置に静止せず、再び負の向きに運動するための\(v_0\)の条件を求めよ
（３）\(v_0\)が（２）の条件を満たすとき、２回目に小物体の速度が０になる時刻を\(t_2\)とする。\(t_1\)から\(t_2\)までの間で速さが最大となる位置を求めよ
（４）時刻\(t_2\)における小物体の位置\(x_2\)を、\(x_1\)を含んだ式で表せ。
（５）以降、このような運動を繰り返す。\(n\)回目に速度が０となる位置\(x_n\)を\(x_1\)を使って表せ。ただし、\(n\)は奇数とする。
（１）最初と最後の状態だけ→「エネルギー保存則」
原点での状態がわかっていて、速度が０になる状態について考える。このように、最初と最後の状態について考えれるときはエネルギー保存則を使うといいよ！！
AKINORI
エネルギー保存則についてはこちら！！
エネルギー保存則は
（はじめの力学的エネルギー）＋（非保存力にされた仕事）
＝（あとの力学的エネルギー）
です。
これを使うために必要な情報を求めておきましょう。
- はじめの力学的エネルギー
これは運動エネルギー\(\frac{1}{2}mv_0^2\)だけです。
- 非保存力にされた仕事
今回の非保存力は動摩擦力です。
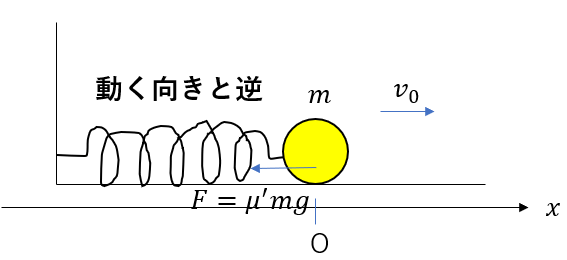
今回は、右向きに動くのに対し、動摩擦力は左向きです。
つまり、仕事は負になります。
\(W = -\mu’ mg \cdot x_1\)
- あとの力学的エネルギー
ばねが\(x_1\)だけ伸びて、静止しているのでばねの弾性力
\(\frac{1}{2}kx_1^2\)
だけですね。
あとは当てはめると
\(\frac{1}{2}mv_0^2 – \mu’ mg x_1 = \frac{1}{2}kx_1^2\)
∴\(\frac{1}{2}kx_1^2 + \mu’ mgx_1 – \frac{1}{2}mv_0^2 = 0\)
これはもう解の公式を使って解くしかないですね。
\(x_1 > 0\)ということに注すると、答えは
\(x_1 = \frac{ – \mu’ mg +\sqrt{(\mu’ mg)^2 + kmv_0^2}}{k}\)
ひや～すごい答え・・・
AI
しょうがないね。こういうこともあるから不安にならないで自信もって答えよう！！
AKINORI
（２）静止するor しない→最大摩擦力に注目！
これは最大摩擦力に注目すればいいんですね！
AI
（１）の状況を考えてみましょう。
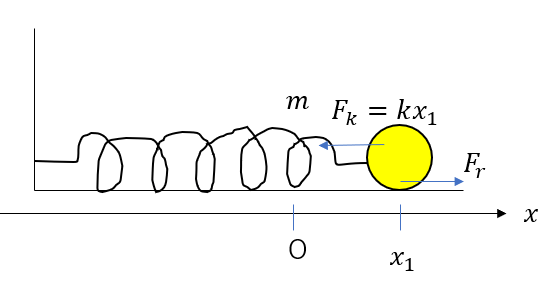
この時、ばねは伸びていますから左向きに弾性力が働き、
左に動こうとしているので、摩擦力は右向きに働きます。
そして、静止する or しない
のようなことを考えるときは、その境目を考えるのがいいです。
つまり、
ギリギリ静止している
この状況を考えてあげましょう。
まず、静止しているから、力がつり合っていますね。
\(F_k = F_r\)
そして、ギリギリ静止しているというのはご存知の通り、
最大摩擦力になっているときです。
つまり\(F_r = \mu mg\)となっている
ということです。
なので、
\(kx_1 = \mu mg\)
さっきの\(x_1\)を代入して、整理していくと・・・
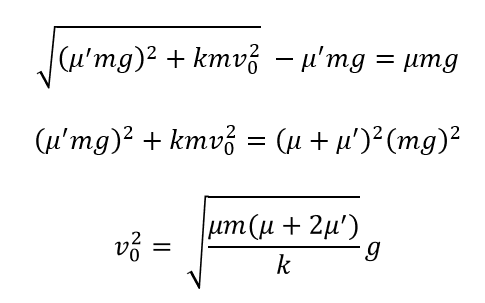
これがギリギリ静止するときの\(v_0\)です。
じゃあ、静止せずに動くには・・・
これより大きければよくないっすか？
ということで、求める条件は
\(v_0 > \sqrt{\frac{\mu m(\mu + 2\mu’)}{k}}g\)
これが（２）の答えです。
（３）単振動の流れをまずやってみよう！
\(x_1\)の位置からまた単振動をするんですよね、おそらく。ならやることは・・・
AKINORI
運動方程式を立てて３ステップをやる！！
AI
単振動については「単振動の問題。運動方程式を立てる流れを詳しく解説！」をチェック！
ではいきます。
運動方程式をまずは立てるんですが、軸はもう定められてるので、力をベクトルで表すんですね。
今回は二つの力が働きます。
まず、摩擦力\(\vec{F_r}\)
これは簡単で、常に右向きに働き、大きさは\(\mu’ mg\)なので
\(\vec{F_r} = (\mu’ mg)\)
です。
次はばねの弾性力\(\vec{F_k}\)ですね。
これは、状況によって向きが変わってしまうので、場合分けです。
- ばねが伸びているとき
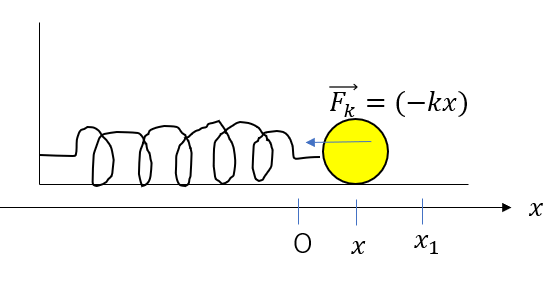
ばねが伸びていると、位置座標\(x\)は正です。
一方、弾性力は左向きにはたらくので、成分をマイナスにしないといけないです。
よって
\(\vec{F_k} = (-kx)\)
と書けます。
- ばねが縮んでいるとき
ばねが縮んでいるとき、位置座標\(x\)は負です。
一方、弾性力は右向きなので、成分は正です。
なので
\(\vec{F_k} = (-kx)\)
と書けます。
ということで、場合分けせずとも
\(\vec{F_k} = (-kx)\)
と書けるんですね。
ここまでくれば、後は合力を求めて運動方程式を立てるだけです。
合力\(\vec{F}\)はとにかく足すんでしたね。
\(\vec{F} = \vec{F_k} + \vec{F_r} = (-kx + \mu’ mg)\)
そして運動方程式\(m\vec{a} = \vec{F}\)に成分を代入して
\(ma = -kx + \mu’ mg\)
∴\(a = -\frac{k}{m} (x – \frac{\mu’ mg}{k})\)
あ！来ましたね！！「\(a = -(定数)\times (xの一次式)\)」
AI
なので、単振動することが分かります。
AKINORI
単振動することがわかったらやるべきことが３つありました。
- 振動の中心を求める
これは\(a = 0\)のときの\(x\)です。
\(x_0 = \frac{\mu’ mg}{k}\)
ですね。
- 角振動数\(\omega\)を求める
これは\(\omega = \sqrt{定数}\)とすればよいので
\(\omega = \sqrt{\frac{k}{m}}\)
- 周期\(T\)を求める
\(T = \frac{2\pi}{\omega}\)と表せるので
\(T = 2\pi \sqrt{\frac{m}{k}}\)
ですね。
問題には関係ないですが、周期まで求めておきました。
そして、単振動の速さが最大になるところですが、それは
振動の中心
です！！
さっき振動の中心は求めましたよね？
それが答えです。
\(x = \frac{\mu’ mg}{k}\)
ですね。
（４）速さが０となるところは振動の端！
これってまた（１）みたいに二次方程式解かないといけない！？
AI
いや、今回はそんなことしなくても大丈夫。速さが０のときって物体は単振動のどの位置にあるの？
AKINORI
あ！振動の端ですね！・・・そっか。振幅を求めればいいんだ！！
AI
速さが最大なのは振動の中心。
速さが０なのは振動の端です。
そして、振動の端になるの場所は
中心から振幅だけずれたところです！！
これが分かれば楽勝ですね。
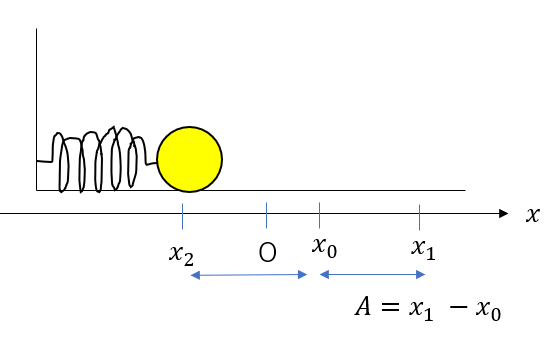
いま考えている単振動は、スタートが\(x_1\)なので、\(x_1\)の位置が振動の端ですね。
つまり振幅は
\(A = x_1 – x_0\)です。
もう一方の振動の端\(x_2\)は中心から左に\(A\)だけずれたところですよね。
\(x_0 – x_2 = A\)
というわけです。
つまり
\(x_2 = 2x_0 – x_1\)
∴\(x_2 = \frac{2\mu’ mg}{k} – x_1\)
これが答えですね。
（５）代表的なものを考えてみる。
う～ん。難しいな・・・
AI
こういう一般に考える問題はとっかかりにくいね。そんなときは、具体的な場合を考えるといいよ！
AKINORI
今\(x_1 \to x_2\)という運動を考えましたね。
同じように\(x_2 \to x_3\)という運動も考えてみましょう。
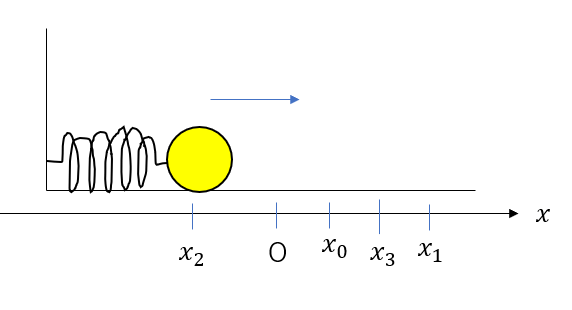
同じように運動方程式を立てていきます。
今度は摩擦力は左向きに働くので
\(\vec{F_r} = (-\mu’ mg)\)
と書けます。
あとは全く同じです。
運動方程式を立てると
\(ma = -kx -\mu’ mg\)
\(a = -\frac{k}{m}(x + \frac{\mu’ mg}{k})\)
やっぱり単振動しますね。
中心は
\(x_0′ = \frac{-\mu’ mg}{k}\)
となっています。
残りのステップは同じなので省略！
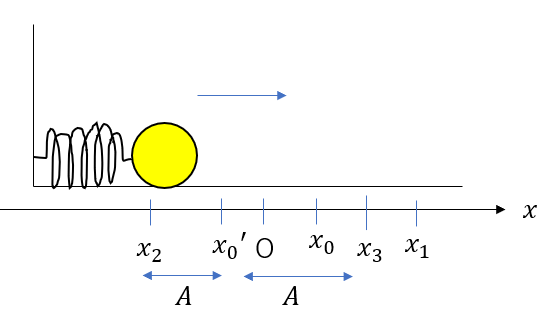
さっきと同じように考えて
\(x_0′ – x_2 = x_3 – x_0’\)
∴\(x_3 = -\frac{\mu’ mg}{k} – x_2\)
となります。
っていうのをどんどん繰り返していくんですね。
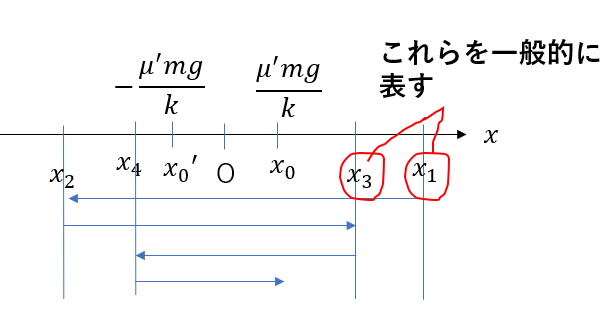
んで、\(n\)は奇数なので、図の赤丸が付いたところを一般的に求めるんです。
で、運動方程式を立てるの式は、往復回数に依らずに同じです。
右→左と移動するときは
\(ma = -kx + \mu’ mg\)
左→右と移動するときは
\(ma = -kx – \mu’ mg\)
と回数に関係なく、こう表せます。
そして、具体的に位置ついて
次のように表せていましたね。
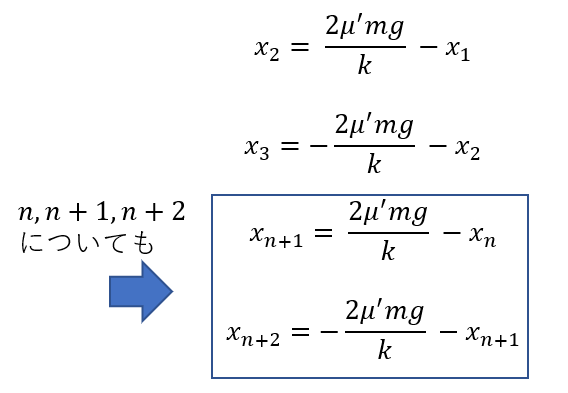
なら、\(n\)についても成り立ちますよね。
だって、運動方程式は同じように立てられるんですから。
\(x_{n + 1}\)を消去して整理すると
\(x_{n + 2} = x_n – 4\frac{\mu’ mg}{k}\)
これはつまり・・・
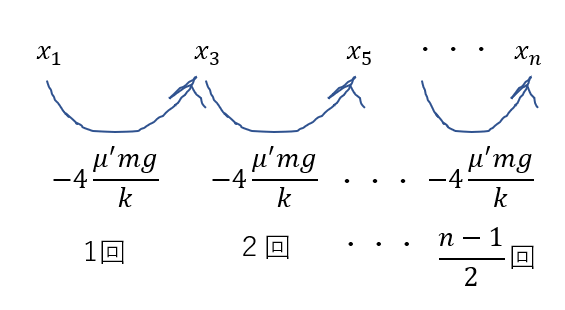
\(x_1\)から始めて
\(\frac{n-1}{2}\cdot (-4\frac{\mu’ mg}{k}\)
\(= -2(n -1)\frac{\mu’ mg}{k}\)
だけ小さくなる。
ということなので
\(x_n = x_1 – 2(n – 1)\frac{\mu’ mg}{k}\)
と表せます。
＊もしくは・・・
初項\(x_1\)、公差\(-4\frac{\mu’ mg}{k}\)の等差数列の一般項は
\(x_n = x_1 + (n -1 ) (-4\frac{\mu’ mg}{k})\)
です。
今回は\(x_{n +2}とx_n\)の式で、項は半分なので
\(n-1を\frac{n-1}{2}\)に置き換える。
このような考え方でもOKです。
最後は難しかったけど、それまではそんなに大したことなかったな～
AI
そうだね。単振動でやるべきことをきっちりやれば摩擦が来ても関係ない！ってことだね。
AKINORI
こんな問題もチャレンジ！
