滑車と張力。滑車が糸から受ける力を詳しく見てみた
糸を滑車に通す。こういう状況はよく見るよね？AIさんはこの時の滑車に働く力を考えたことってありますか？？
AKINORI
滑車にかかる力？う～ん、考えてないかもです。それがどうかしたんですか？
AI
実は、滑車の力って考えておかないとヤバいときがあるんだ！ということで、今日は滑車と糸について考えていこう！！
AKINORI
僕に、こんな質問が来ました。
下の状況でなんで、外力を加えていると物体Cは動かないんですか？
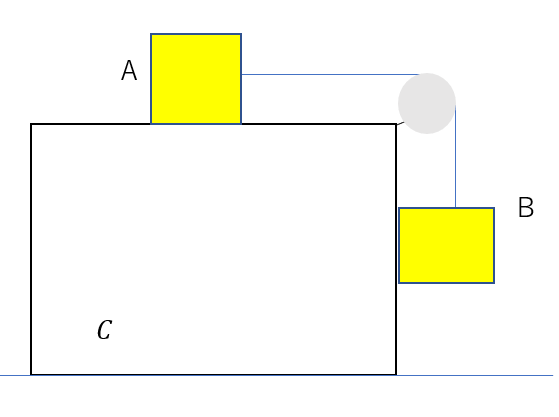
A,Bは滑らかな滑車を通して糸でつながっています。また、Cも床に固定されているわけではないので、力を加えることで動かしたりできます。すべての面で摩擦はないとしますね。
さて、この状態で外から何も力を加えないと、Cはどうなると思いますか？？
・・・え？止まったままなんじゃ・・？
AI
違います！
この場合、右向きに力を加えないとCは動いてしまいます。
これには、滑車が関係しています。
滑車も力を受ける？？
Cに働く力を考えて見ましょう。
とりあえず、ここまではわかりますね。
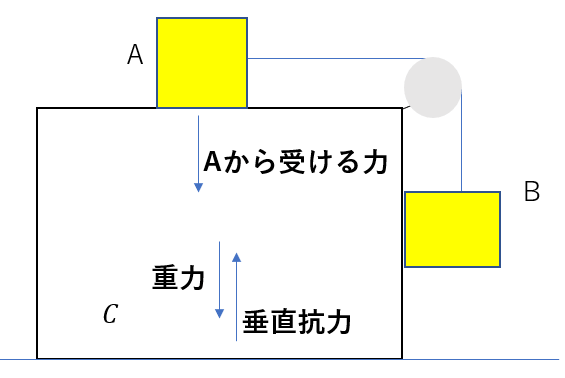
実は、まだ力はあります。
それは
滑車が糸から受ける力です。
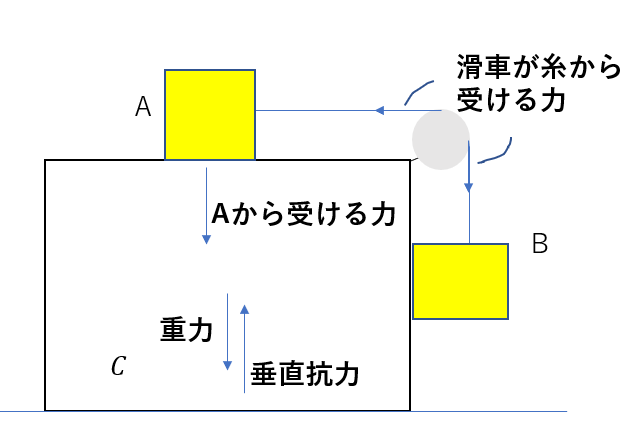
このように、滑車は糸から
・水平右向き
・鉛直下向き
の力を受けます。
これを見れば明らかですね。
このままだと左向きに動く！！
というわけで、右向きに外力を加えないと静止させることができないわけですね。
なるほど！滑車の力も考える必要があるんですね！
AI
Cが固定されていれば、Cについては考える必要があまりないので、滑車の受ける力を考える必要はないんだね。
AKINORI
なんで滑車は力を受けるの！？
でも、そもそもなんで滑車に力が働くんですか？別に摩擦があるわけじゃないですよね？
AI
そうだね。そこを詳しく見ていこう！
AKINORI
とりあえず、滑車には力が働くよ～
っていうのはわかりましたか？
まあ、そんなのはどうでも良くて（笑）
なんで滑車にはさっきのような力が働くの？？
っていうのを考えていきます。ここが大事です。
これが今日のメインですね。
ではいきます！
ひもを細かく分解してみる
滑車とひもはこういう状態になっています。
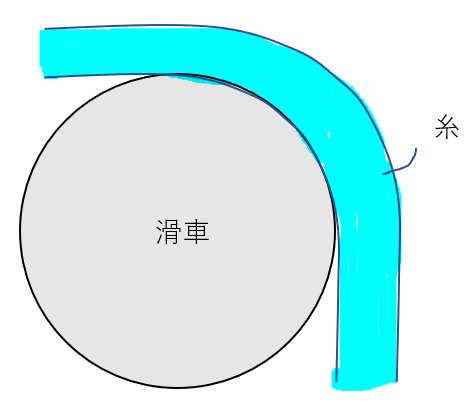
拡大図です。
ひもが滑車に乗っているので、滑車はひもから力を受けますね。
しかし、いろんな面から力を受けるので、結果的にどんな力が働くのかを考えるのは難しいです。
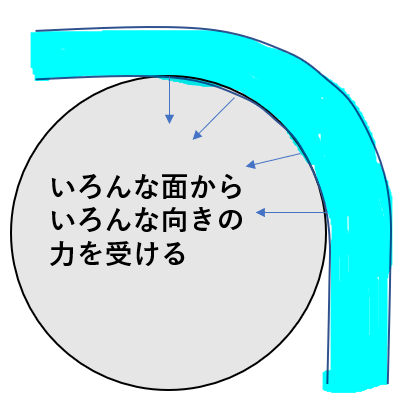
ということで、このひもを細かく分割していきます。
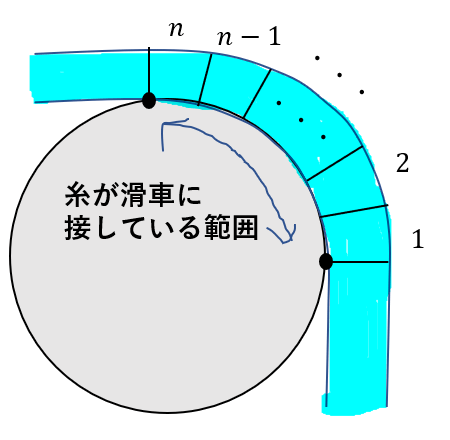
こんな感じで、滑車に接している糸を\(n\)個に分けて、番号をつけていきます。
そうすると、滑車の受ける力は
各ブロックから受ける力を足し合わせたもの
ですよね。
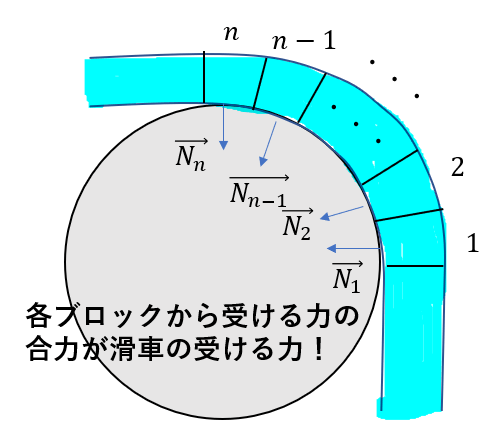
つまり、図のように、各ブロックから受ける力を
\(\vec{N_1}, … , \vec{N_n}\)
としたら、その合力
\(\vec{F} = \vec{N_1} + … + \vec{N_n}\)
を求めればいいということです。
＊以降はベクトルが重要になってくるので、ベクトルについてはこちらを見ておいてください！
ここで、糸の各ブロックが受ける力を考えて見ましょう。
まずはブロック１です。
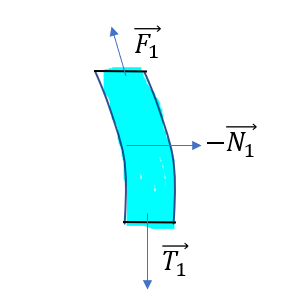
ブロック１には３つの力がはたらきます。
- 滑車から受ける力
これは、さっき滑車が受ける力を\(\vec{N_1}\)としたので、
糸が滑車から受ける力は
\(-\vec{N_1}\)
となりますね。
マイナスは向きが逆という意味を表しています。
- 下側の糸から受ける力\(\vec{T_1}\)
- ブロック２から受ける力\(\vec{F_1}\)
という風に力を考えることができますね。
次にブロック２についても考えて見ると。。。
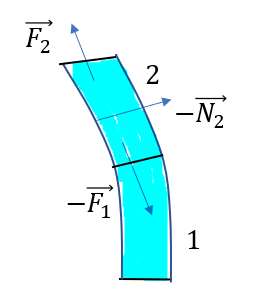
ブロック１の場合とほとんど同じです。
- 滑車から受ける力\(-\vec{N_2}\)
- ブロック１から受ける力\(-\vec{F_1}\)
- ブロック３から受ける力\(\vec{F_2}\)
と、こんな感じですね。
これを\(n\)個目まで同じようにやっていきます。
ここまで良いですか？
さて、このブロックをつなげれば糸全体になりますよね。
この糸は軽い糸、つまり質量を無視しています。
質量を無視できるとき、糸に働く合力は０です。（力がつり合っている）。
これについてはこちらをチェックしてください。
\(m\vec{a} = \vec{F}\)
の\(m = 0\)を考えれば
\(\vec{F} = 0\)ですね。
ですから、合力は０です。
というわけで、糸の合力を考えていきます。
が、これはすごくきれいな形になります。
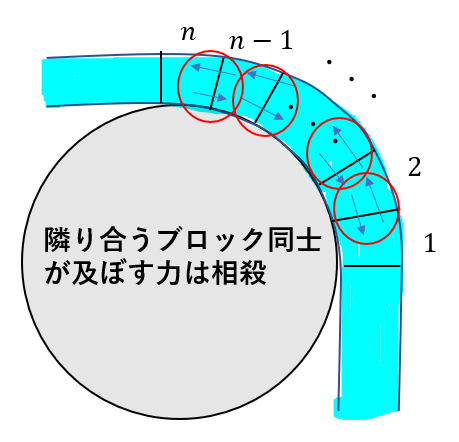
各ブロックが及ぼしあう力は作用反作用の関係にあるので、
足し合わせるとこの力は相殺されます！
なので、考えるべき力は
- 滑車から受ける力
- 滑車に接していない糸から受ける力
ですね。
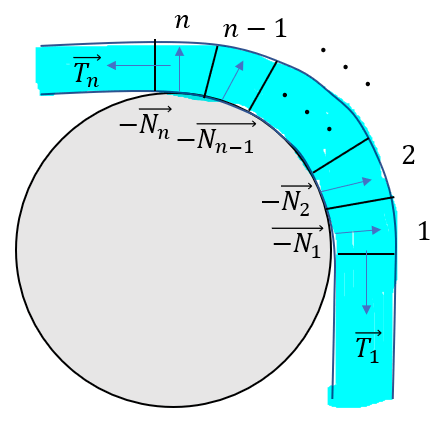
これらの合力が０になりますから
\(\vec{T_1} + \vec{T_n} + (-\vec{N_1}) + … + (-\vec{N_n}) = 0\)
合力はとにかくベクトルを足す！！
これがポイントでした。
詳しい話はこちらで
今立てた式を変形します。
\(\vec{N_1} + … + \vec{N_n} = \vec{T_1} + \vec{T_n}\)
あれ？左辺ってまさに滑車が受ける力だ！
AI
そう。そして、右辺はどんな力だった？
AKINORI
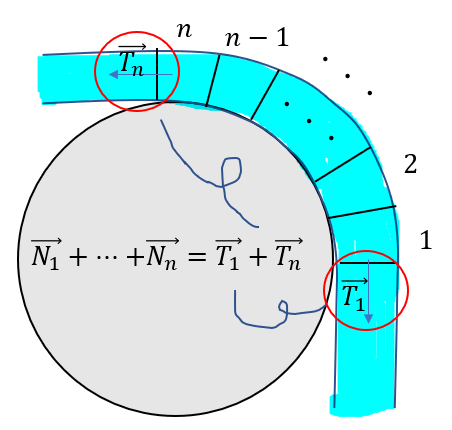
下向きの力と上向きの力です！！
AI
わかりましたね。滑車が受ける力は
滑車に接していない部分の糸が引っ張る力
というわけです。
なので、最初に考えたこの状態では、
滑車に左向きの力と下向きの力がかかるわけです。
これらの力の大きさは張力の大きさ\(T\)でともに等しいです。
なるほど！滑車と糸について詳しく見てみると、滑車が力を受けることがわかるんですね！
AI
そう！また、滑車との摩擦が無くても力が働いているのが今のでわかるね。
AKINORI
