円の切り抜き図形の重心の求め方！「公式？そんなの使わんよ」

2019年2月24日

2019年12月14日

WRITER

あっきー

　

この記事を書いている人 - WRITER -

あっきー

オンライン物理塾長あっきー。高3秋から1か月で40点点上げ、センター試験では満点を取り、その経験を活かし塾講師として活躍。塾・学校・参考書の内容やカリキュラムに違和感を感じ数多くの高校生を救うため、大学2年生で「受験物理Set Up」を開設。多くの高校生が活用するサイトに発展し、現在「合格への道」で勉強法に特化した受験サポートを行う。

今回はこのような悩みを解決していきます。

よくある重心を求める問題。その中でも、図形がちょっといびつなパターンは厄介ですよね。

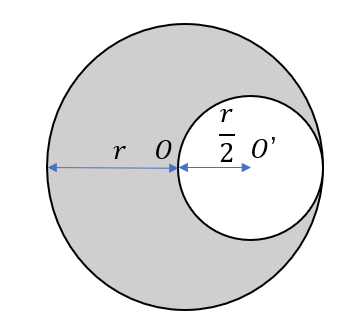
↑こういうやつ

そして、なんか知らないけど、教科書とかでは大々的に公式が発表されてます。

\(x_g = \frac{m_1x_1 + m_2x_2 + …}{m_1 + m_2 + …}\)

ですが悲報です。これ、全く使えません！！

使おうとすると、圧倒的に悩みます。

ポイントは公式に当てはめるのではなく、重心を求める過程をそのまま適用しましょう。

くり抜き図形の重心の求め方とは

重心の公式は紹介されていますが大事なのは重心の性質を理解することです。
重心のポイントは「質量の代表点」ということです。

質量の代表点ということから、重力に関する様々なことを代表するのです（すごい抽象的ですが）。

つまり複数の物体の重力がその点に働き、かつそのモーメントの和も重心の重力が代表するというわけです。

たぶんこの説明をしても意味が分からないと思うので以下の記事をまずは読んでくださいね。

物理の重心とは？【重心の求め方に公式はありません！】

2019-02-18

円のくり抜き図形の重心を求めてみよう

では、実際にさっきの図形の重心を求めてみましょう。

この問題のポイントは・・・切り抜いた図形を戻せば、元の図形に戻る！！ということです。

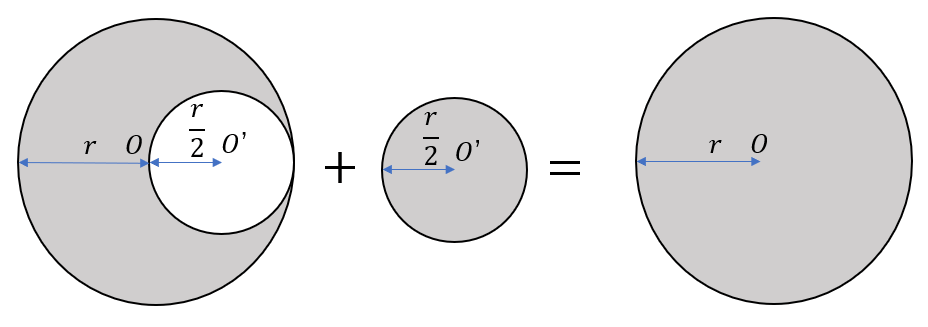
こんな感じです。

さて、ここで、重要なのはそれぞれの図形がどの位置にどれだけの重力がかかっているか？ということです。

これは、最初で紹介した記事でのお話です。それが分かれば、重心の特徴である「代表点」の性質、
つまり、「モーメント代表」ということを使えば解けそうですね。

なので、各図形の重力について考えてみましょう。

円のそれぞれの重心と重力を求める

まず。結論から示しちゃいます。

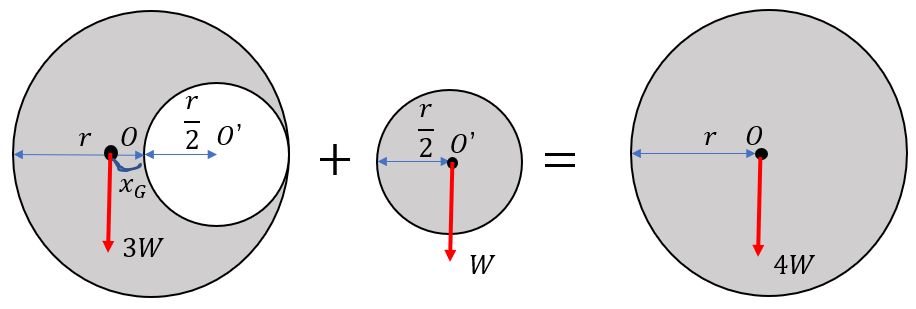
こういう関係図が見えてくれば解けたも同然です

それぞれ見ていきますね。

真ん中の図形について

真ん中の重さを\(W\)とすると、この図形は「円」なので、重心も中心O’になることは当たり前ですね。

ですから、図のように書けるわけです。

右の図形について

次は右の図形です。

まず、重さ（重力の大きさ）を考えます。

この図形は一様ですから、重さは何で決まると思いますか？

そうです、面積に比例しますね。

例えば面積当たりの質量（密度）を\(\rho\)とすれば面積を\(S\)として質量は\(m = \rho S\)と書けますね。

なので、重さ（重力）は面積に比例します。

今、「半径\(\frac{r}{2}\)の円の重さが\(W\)」なわけですね。ということで「半径\(r\)の円板の重さ」は・・・

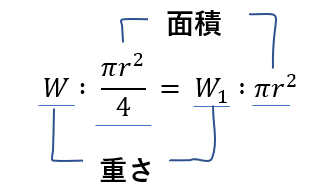
こういう比例式で解けますね。

「\(\frac{\pi r^2}{4}\)の面積で\(W\)の重さ。

では、\(\pi r^2\)の面積での重さ\(W_1\)は？？」こういうことです。

なので、\(W_1 = 4W\)となります。

そして、この図形の重心の位置ですが、これもきれいな「円」なので円の中心が重心ですね。ですから、図のようになるわけです。

左の図形について

最後に、左の図形について考えましょう。

まずは、重さです。

これは、右の円板から真ん中の円板を引けばいいので
\(4W – W  = 3W\)ですね。

次に重心ですが、これを求めたいので適当に定めます。

今回は「点Ｏから左に\(x_G\)だけずれた位置」としておきましょう。

以上をまとめると、結論通りになりますね。

重心の求めるポイントは「重力の代表点」

このように、「二つの図形を足せば、元の図形に戻る」ということであれば

「二つのモーメントを足せば、もとのモーメントに戻る」こういうことですね。

そこで、「点Ｏ周りのモーメント」を考えてみましょう。

各図形のモーメントを求める

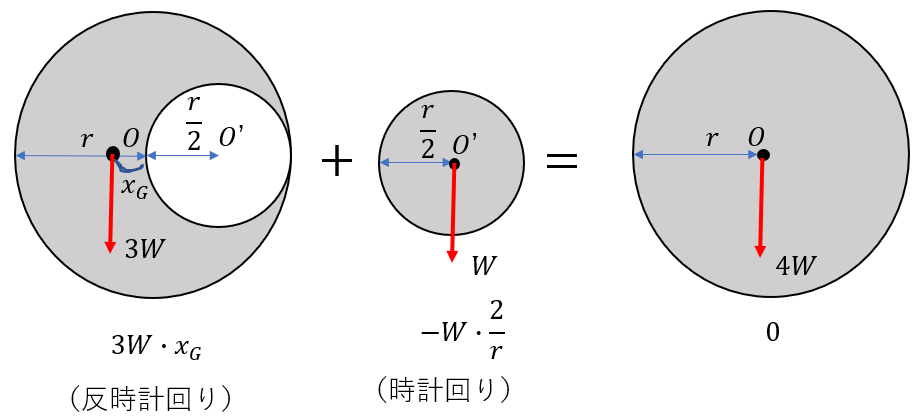
モーメントの大きさは「力×長さ」でしたね。

正確には、「長さ」は「基準点から力の作用線までの長さ」でした。

また、向きは「反時計回りを正」と定めるんでしたね。

左の図形では点Ｏ周りでは反時計回りに回るので正です。

なので、モーメントは\(3W・x_G\)です。

同様に、真ん中の図形は時計回りなので負です。なので、モーメントは
\(W・\frac{r}{2}\)です。

右の図形は基準点に重力が働いているので当然モーメントは0です。

「重力の代表点」利用

各重力によるモーメントが求められました。

あとは、それぞれモーメントを足したら代表のやつと一致するので
\(3Wx_G + (-W\frac{r}{2} = 0\)
です。

つまり
\(x_G= \frac{r}{6}\)
ということになります。

「点Ｏから左に\(\frac{r}{6}\)の位置」ということになりますね。

このように公式を使うのではなく、重心の性質を使うことで求めることが大事です。

\(x_G\)がマイナスで現れたら？

実は、\(x_G\)はマイナスの値で出てくることもあります。

例えば、この問題で点Ｏの右側に重心を取って見るとどうでしょう？？

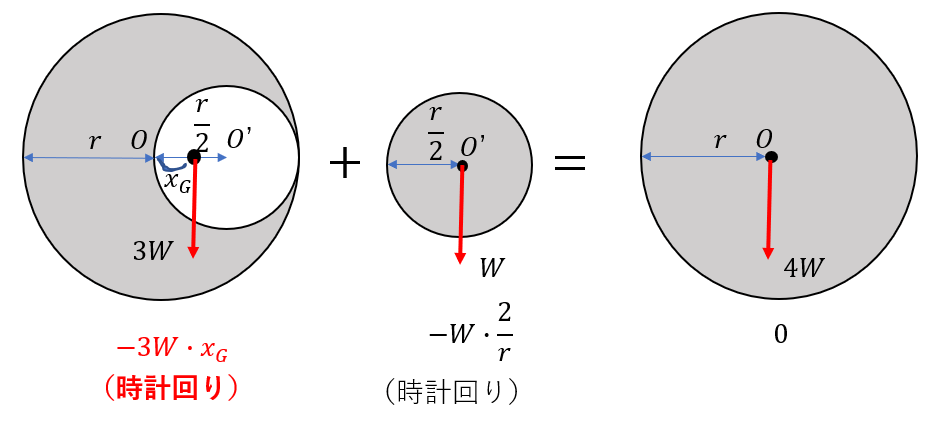
このように、左の図形について、モーメントが負になりますね。

同じように解くと
\(x_G = -\frac{r}{6}\)
が出てきます。

マイナスが出てきてしまいますね。

このマイナスは「逆向き」という意味です。

つまり、最初に仮定した向きとは逆向きに重心の位置があるということになります。

なので、答えは同じになります。

まとめ：円形のくり抜き図形の重心

いかがでしたか？

このように公式を使うのではなく、重心の性質を使った解き方を意識しましょう。

そのようにすれば、どんな問題でも悩むことなく解くことができます。