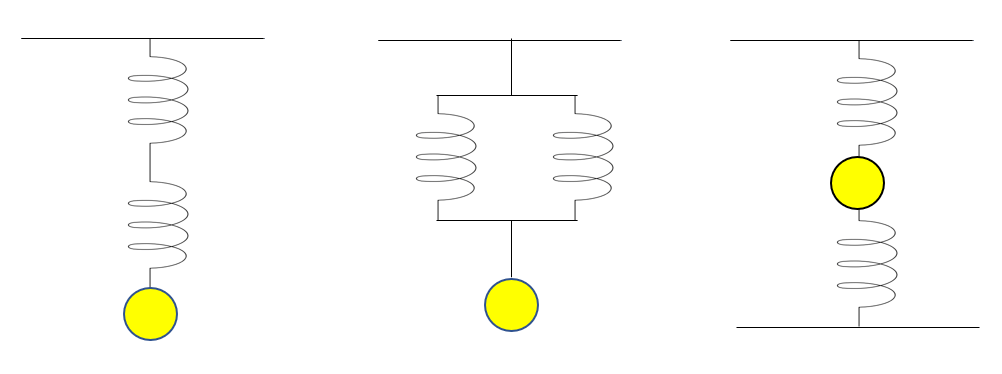
合成ばね定数とは？ばねの直列・並列の扱い方を教えます！

物理の問題集の解説で納得がいかないランキング上位に入るのが、二つのばねについての解説です。

いわゆる合成ばね定数なのですが、問題集ではこんな解説が乗っていました。

ばね定数$k_1, k_2$の二つのばねを連結させ、それらを１つのものとみなしたときのばね定数（合成ばね定数）は、次式で表される。

• 直列型 $\frac{1}{k} = \frac{1}{k_1} + \frac{1}{k_2}$
• 並列型 $k = k_1 + k_2$
• サンドイッチ型 $k = k_1 + k_2$

これ見て思うのが、「それどっから出てきた？」ということですよね。

実はこれは暗記するものではなく、むしろ合成ばね定数を求める過程が大事になってきます。

今回は合成ばね定数の導出の仕方を解説していきますね。

合成ばね定数とは？

そもそも合成ばね定数とは何か簡単にお話します。

「合成」と言ってますが、ただばねをつなぎ合わせるという意味ではありません。複数のばねを1つのばねに置き換え変えることをばねの合成と呼ぶんです。

コンデンサーの合成容量や抵抗の合成も同じです。

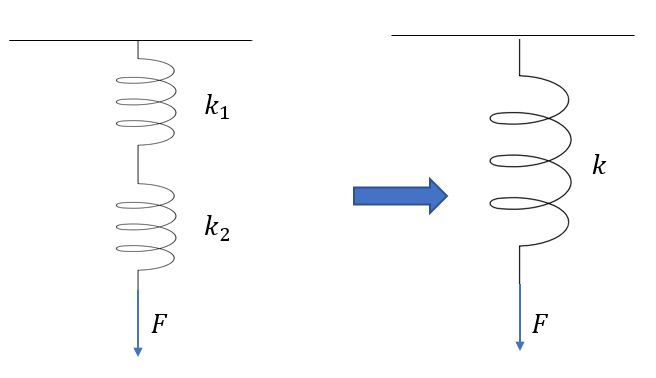
イメージはこうですね。

2つのバネにおいてフックの法則を利用し、条件式を整理したうえで性質を変えないようにばね1つに置き換えます。

この時のばね定数を合成ばね定数と呼ぶのです。

それでは、3つの場合それぞれで合成ばね定数を考えていきましょう。

合成ばね定数の導出1：直列接続

---

ばね定数$k_1, k_2$の軽いばねが図のように連結している。このばねの端を大きさ$F$で引っ張る。ばねを一つに見たときのばね定数を求めよ。なお、ばねは静止しているとする。

---

ばねを一つにみなした場合のばね定数を求めます。

ばねの弾性力の大きさを考えると、合成したばねの伸びが$x$となったときに

$F = kx$

と表せますよね。

この式の形を$k$の代わりに、$k_1, k_2$で表してやろう！！ということです。

直列ばねの条件式1：ばねの伸びについて

ばねの伸びをそれぞれ$x_1, x_2$としたときに、合成ばねの伸び$x$は

$x = x_1 + x_2$

ですよね。

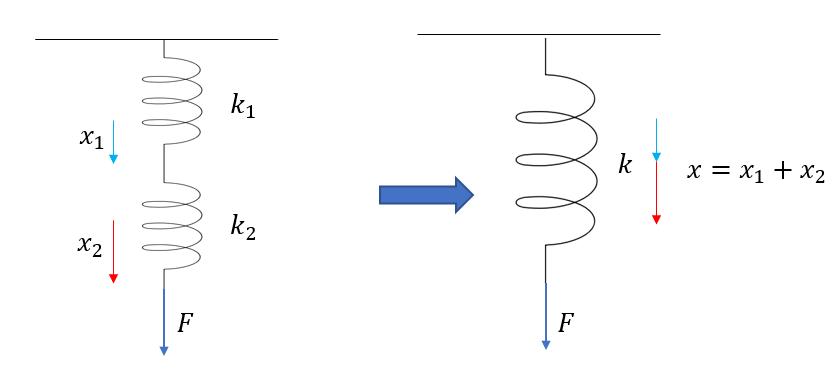
図を見れば一目瞭然ですね！

この状況から

$F = kx$

の形を目指します。

直列ばねの条件式2：弾性力について

さてさて、下のばねについては$F$の力を受けていますが、これはフックの法則から

$F = k_2 x_2$

と書けます。

そして、今回のばねは「軽いばね」です。

「軽い」というのは質量がないという意味ですね。なので、ばねの反対側にも同じ大きさで逆向きの力が生じます。

その理由は運動方程式を立てると分かりますね。

ばねについて運動方程式を立ててみると

$m\vec{a} = \vec{F}$

ですが、「軽い」ので$m = 0$とすると、

$\vec{F} = 0$

合力が０なんですね。

ばねには合力が０となるように力が働いていないといけません。そのためには、両端が同じ大きさで逆向きに力が働かないといけませんね。

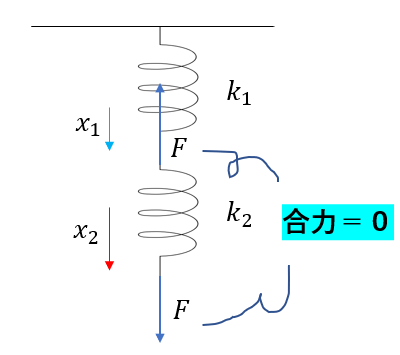
こんな感じ。

ここまでは下のばねについてのお話です。

次は上のばねについて考えます。

先ほど書いた、力をよく考えてください。

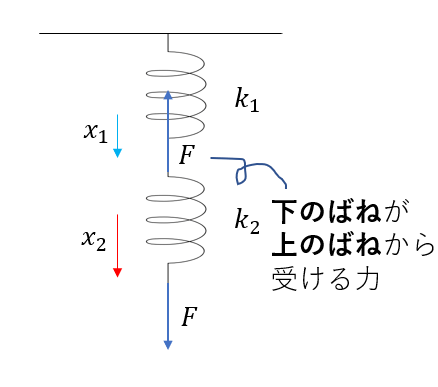
この力は下のばねが上のばねから受ける力です。

つまり、上のばねが下のばねから受ける力もあるわけです。

つまり作用反作用の法則です。

そして、これは

• 大きさが同じで
• 向きが逆

でしたね。

つまり、

上のばねにも同じ大きさ$F$の弾性力が働いているわけです！！

ですから

$F = k_1 x_1$

と書けるんですね。

条件式から直列ばねの合成ばね定数を求める

さて、ここまで2式が得られました

• $F = k_1x_1$
• $F = k_2x_2$

これを$F = kx$の形にもっていきます。

まず、得られた式を変形しましょう。

• $x_1 = \frac{F}{k_1}$
• $x_2 = \frac{F}{k_2}$

そして、両辺を足します。

$x_1 + x_2 = F\left(\frac{1}{k_1} + \frac{1}{k_2}\right)$

ここで$x_1 + x_2 = x$ですね。

次に$\frac{1}{k_1} + \frac{1}{k_2} = \frac{1}{k}$とおくと

$$x = \frac{F}{k}\\ \Rightarrow F = kx\\ (\dfrac{1}{k} = \dfrac{1}{k_1} + \dfrac{1}{k_2})$$

$k$も$x$も1つのばねに置き換えたときの量で、かつフックの法則の形になっていますので、置き換えに成功できました。

この$k$が合成ばね定数ですが、さっき置いた通りです。

$\dfrac{1}{k} = \dfrac{1}{k_1} + \dfrac{1}{k_2}$

これが、いわゆる「直列ばねの合成ばね定数」ってわけです。

このように、導出する過程には

• 運動方程式（力のつり合い）
• 作用反作用
• 式利用

などの様々なテクニック(?)が出てくるので、導出するとこういう適用する力も伸びるので暗記しないでいつでも出せるようにしてください。

合成ばね定数の導出2：並列接続

ばね定数$k_1, k_2$の軽いばねが図のように連結している。このばねの端を大きさ$F$で引っ張る。ばねを一つに見たときのばね定数を求めよ。なお、ばねは静止しているとする。

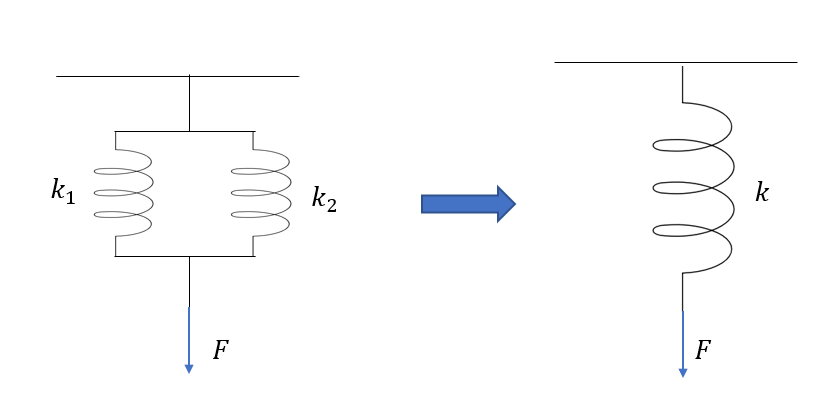
これも直列の場合と同じように、

合成したばねの伸びを$x$としたとき

$F = kx$

という式を目指せばいいですね。

並列ばねの条件式1：ばねの伸びについて

今回、並列につないだ場合、ばねは同じ伸びになります。

もし、ばねの伸びが違っていたらこのばねはゆがんでしまいますね。

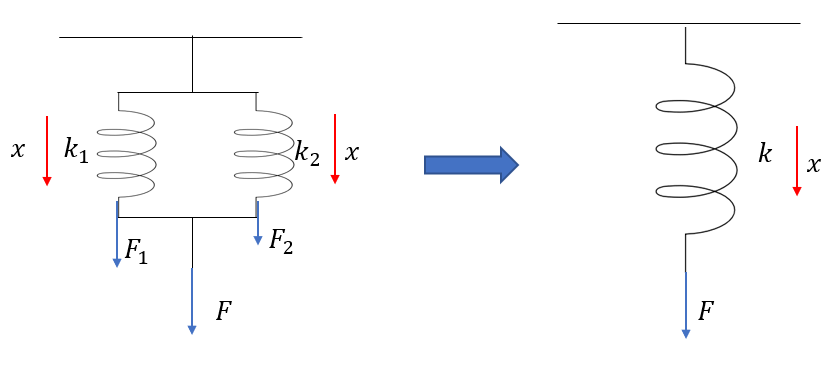
こんな感じで、それぞれのばねの伸びが、合成したばねの伸びと同じになるってことです。

並列ばねの条件式2：弾性力について

ただ、それぞれの弾性力の大きさは異なります。

しかし、

$F = F_1 + F_2$

となるのは図からもイメージが付くでしょう。

それぞれの弾性力の大きさを$F_1 ,F_2$とすると

• $F_1 = k_1 x$
• $F_2 = k_2 x$

ですね。

条件式から並列ばねの合成ばね定数を求める

そして、$F = kx$の形を目指すために、両辺を足します。

$F_1 + F_2 = (k_1 + k_2)x$

そして

$F = F_1 + F_2$,$k_1 + k_2 = k$

とおくと

$F = kx$

となりますね。

$k$も$x$も1つのばねに置き換えたときの量で、かつフックの法則の形になっています。ですから置き換えに成功できました。

改めて並列の合成ばね定数は

$k = k_1 + k_2$

となります。

もちろん、覚えるものではないです。いつでも出せるようにしておくのが重要です。

合成ばね定数の導出3：サンドイッチ接続

ばね定数$k_1, k_2$の軽いばねが図のように、物体を挟んで連結している（このとき、二つのばねは自然長である）。この物体を大きさ$F$の力で下向きに引っ張る。ばねを一つに見たときのばね定数を求めよ。なお、物体の重力は無視し、物体は静止しているとする。

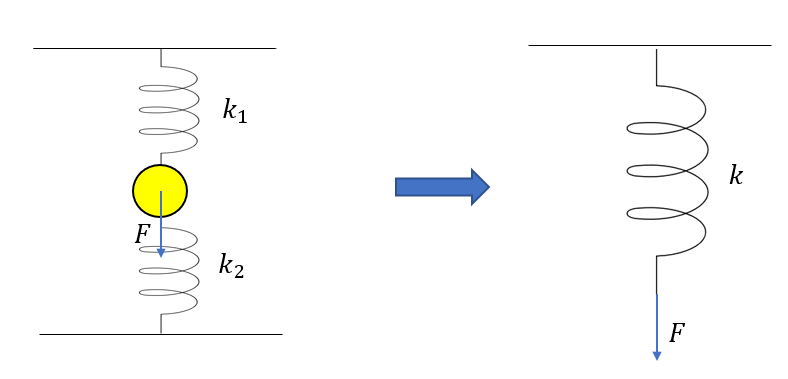
これも今までと全く同じです。

サンドイッチばねの条件式1：ばねの伸びについて

今回、上のばねが伸びて、下のばねが縮みますね。

では、全体の伸びは？・・・

というと今回、ばねは両端が完全に固定されています。

ですから、全体のばねの長さは変化してはいけません。

つまり、上のばねが$x$だけ伸びたら、下のは$x$だけ縮まないといけないのです！！

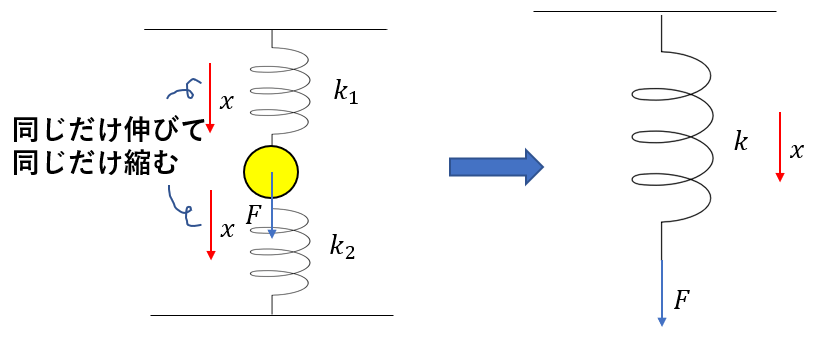
たぶんここで、「一つに見た場合、ばねの伸びが０になっちゃいません？？」と思うかもしれませんが、もう一度合成の意味を考えましょう。

合成はただつなげるだけではなく、あくまで*どんなばねと同じ働きをするのかな？」っていうことを考えるだけです。

合成したばねの伸びが$x$であれば、それぞれのばねの伸びも$x$になっても別に問題ありません。

サンドイッチばねの条件式1：弾性力について

ということで、力を図示して見るとこうなります。

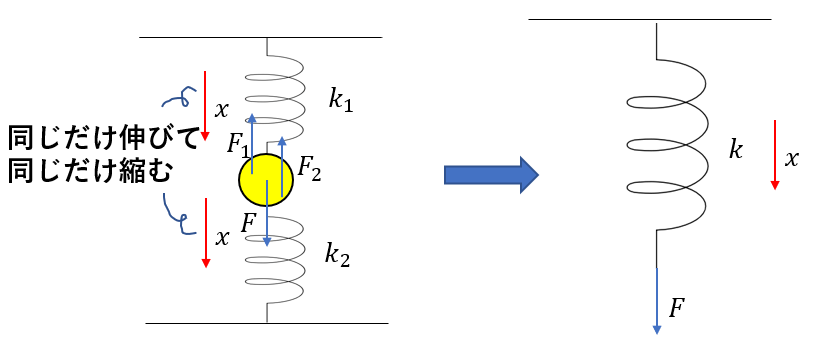
力のつり合いから

$F = F_1 + F_2$

です。

まさに\(F\)は各ばねの弾性力の和になってますね。ですから、これがばねを合成したときの弾性力の大きさになるんです。

条件式からサンドイッチ型の合成ばね定数を求める

そして

• $F_1 = k_1x$
• $F_2 = k_2x$

ということなので

$F = (k_1 + k_2)x$

となります。

これも$k = k_1 + k_2$と置けば

$F = kx$

と表せます。

$k$も$x$も1つのばねに置き換えたときの量で、かつフックの法則の形になっています。ですから置き換えに成功できました。

改めてサンドイッチ型のの合成ばね定数は

$k = k_1 + k_2$

となります。

うるさいようですが、覚えるものではありません！

まとめ：合成ばね定数の導出

このように、ばねの合成ばね定数は覚えるべきじゃないです！

むしろ、このプロセスをきちんとマスターしてください。

この考え方はコンデンサーの合成や抵抗の合成、それ以外でも使えます。

ついでに「コンデンサーの合成容量は複雑？直列とか並列とか気にするな！」や「合成抵抗の求め方。複雑な問題でも求めるコツを大公開します！」も読んでくださいね。

合成ばね定数を求めるプロセス

1. ばねの伸びの条件
2. 弾性力の条件
3. 条件式を使って$F = kx$の形にする