コンデンサーの合成容量は複雑?直列とか並列とか気にするな!

合成容量の意味が分かる
合成容量の導出方法が分かる
合成容量の公式を暗記する必要がなくなる
どうもです!
教科書や参考書、そして問題集を見るとよくこんな説明を見ます。
コンデンサーの合成容量
直列接続:\(\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + …\)
並列接続:\(C = C_1 + C_2 + …\)
僕はこれを見て疑問に思うわけです。
なんで場合分けしてんの?
合成容量の式なんて暗記しなくていいのにわざわざ暗記させられ、
「合成抵抗とは逆になりますよ~」
なんて言われたら、それは問題に出されたときに間違えます。
コンデンサーの問題には解き方があるという話をしました。
合成容量はその延長にあるだけのことなんです。
「直列だからこう、並列だからこう」ではないんです。
今回は合成容量というものがそもそも何なのか暴いていって合成容量の求め方を見せたいと思います。
合成容量の意味とは?

そもそもコンデンサーを合成するってどういうことですか?
 AIさん
AIさん
複数のコンデンサーを一つにまとめることだね。
 あっきー
あっきー
例えば次のような回路があったとします。

コンデンサーが二つありますね。
今回の回路は複雑ではありませんが、できればコンデンサーの数を減らして単純にできた方がいいですよね。
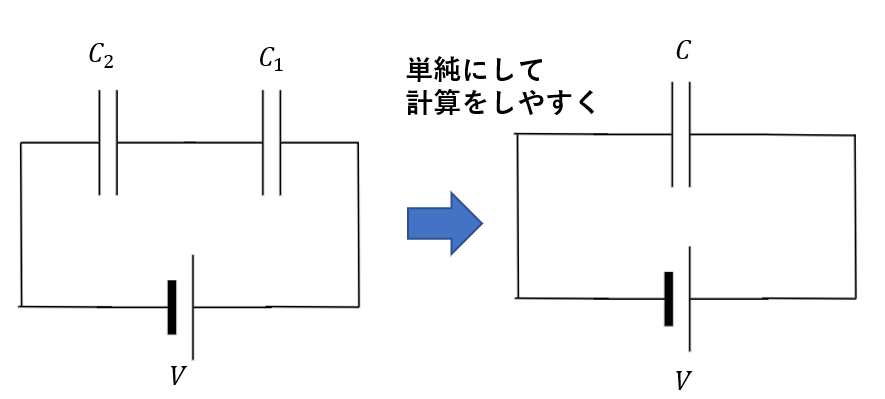
2つのコンデンサーを1つのコンデンサーにみなしたとき、そのコンデンサーの合成容量はどう表されるか?
というのを考えるのです。
これを式で考えていくのですが、ゴールが分からないと意味がないですね。そこで、先にどういう式を最終的に導けばいいのかを教えておきます。
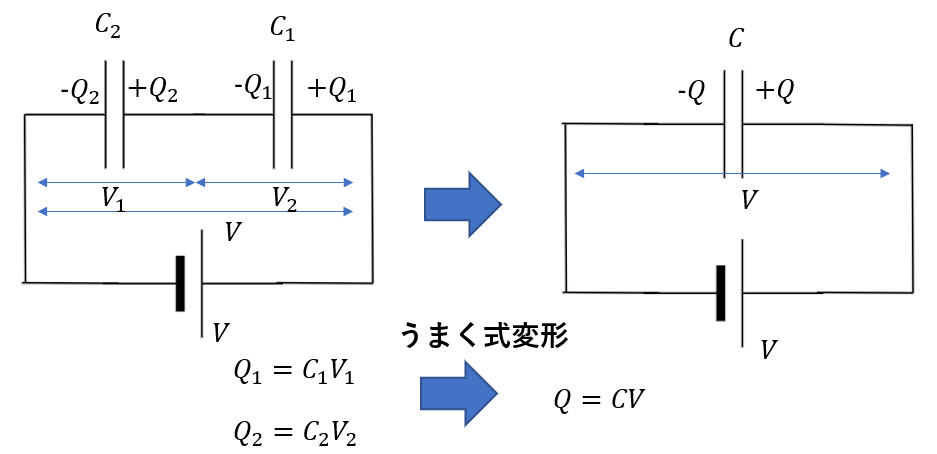
コンデンサーを合成したときに電荷\(Q\)、電気容量\(C\)としたときに
\(Q = CV\)というのが成り立つのは分かりますね。
もともとの回路における、各コンデンサーに関する式
\(Q_1 = C_1 V_ 1\)
\(Q_2 = C_2 V_2\)
から、この式を導いてやるのです。
その時の\(C\)に当たるものがまさに合成容量と言えるわけですね。
複雑じゃない!やることはこれだけ

合成容量を導出していくわけですが、
結局はこれって、コンデンサーの回路に他ならないわけです。
ですからやることは決まっているのです。
電荷保存則
キルヒホッフの法則
これが土台としてあって、後は式操作で現象を解釈する。ただそれだけの話なんですね。
コンデンサー回路についてはこちらをご覧くださいね。
それを踏まえて実際に合成容量を求めてみましょう。
直列接続

図のような回路において、コンデンサーの合成容量を求めよ。

まずは、コンデンサーに蓄えられる電荷を設定します。
ここで注目するのは「電荷保存則」、つまり「島」です。
今回は島がありますね。
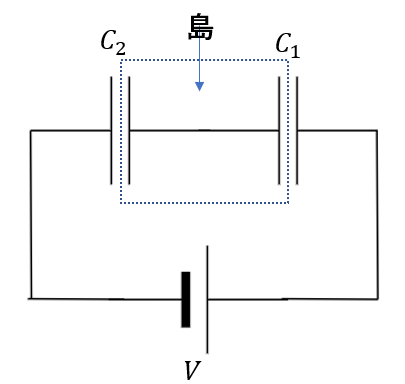
つまり、この部分の電荷の総和は常に一定なわけです。
最初はコンデンサーに電荷が蓄えられていないので、充電完了後もこの点線部分の電荷の総和は0になっていないといけません。
それを踏まえて電荷を設定していくとこうなります。
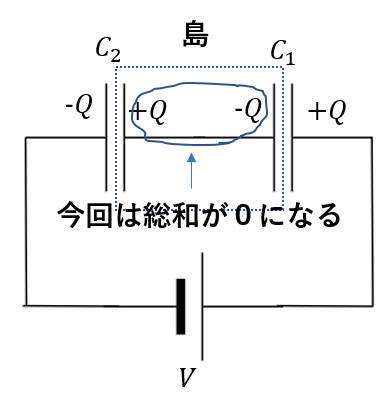
これができたら、後はこれを元に電圧マークを考えて一周します。
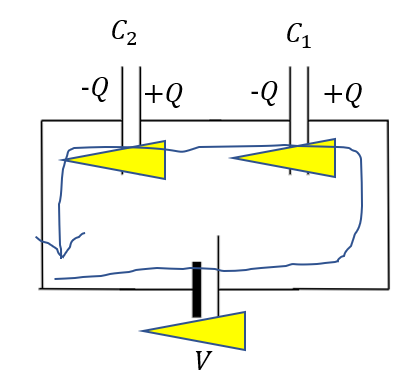
「一周した電位=0」なので
\(V – \frac{Q}{C_1} – \frac{Q}{C_2} = 0\)
\(Q =\frac{1}{\frac{1}{C_1} + \frac{1}{C_2}}V\)
あ!\(Q = CV\)の形になってます!
 AI
AI
\(\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2}\)
と置けば
\(Q = CV\)となりますね。
ということで直列接続のときの合成容量\(C\)は
\(\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2}\)
と表されます。
並列接続

並列の場合も全く同じです。
図のような回路において、コンデンサーの合成容量を求めよ。
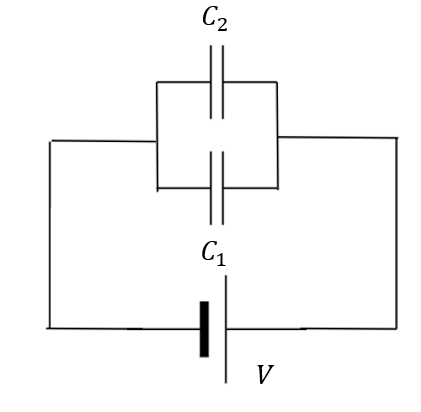
まずは電荷を定めます。先ほどのような「島」は見つからないので電荷量は異なりますね。
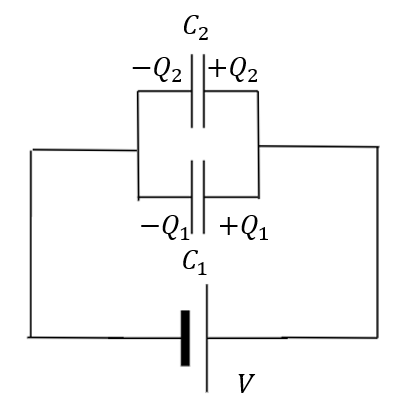
後は電圧マークを設定して一周します。
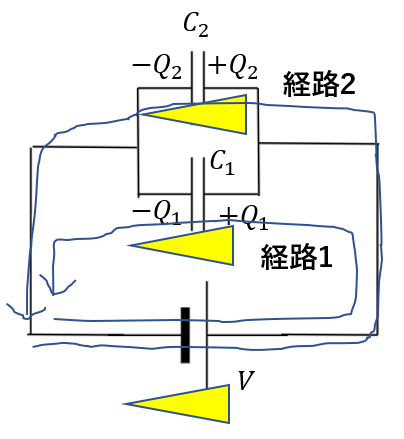
今回は二つの経路を設定しますね。
経路1:\(V – V_1 = 0\)
経路2:\(V – V_2 = 0\)
となります。つまり
\(V = \frac{Q_1}{C_1}\)
\(V = \frac{Q_2}{C_2}\)
です。
今回、1つのコンデンサーに合成すると電荷量はそれぞれの電荷の合計になるのはイメージがつきますね。
つまり
\(Q = Q_1 + Q_2\)です。
これと先ほどの式を合わせると
\(Q = C_1V + C_2V\)
\(Q = (C_1 + C_2)V\)
これも、\(Q = CV\)の形になってますね!
 AI
AI
\(C = C_1 + C_2\)と置けば
\(Q = CV\)
となりますね。
つまり、並列接続のときの合成容量は
\(C = C_1 + C_2\)
となります。
このように直列・並列ともに合成容量を導くことができました。
抵抗・ばねでも考え方は同じ

実は「合成」というのはコンデンサー以外にもいろいろ出てきますね。
合成抵抗
これはすべて「合成」です。
どれも同じように合成したときの式(今回でいえば\(Q = CV\))の形にするために最初の条件から式変形していけば簡単に合成ができます。
それぞれ記事で書いていますので、みてくださいね。
公式は絶対に覚えるな

いかがでしたか?
合成容量は公式で覚えるものではありません。
あくまで
・電荷保存則
・キルヒホッフの法則
を使った延長にすぎません。
常に導出をできるように心がけましょう。









