【高校物理】たったの2ステップ！コンデンサーの問題の究極解法を大公開
どうも！オンライン物理塾長あっきーです
オンライン物理塾長あっきー
コンデンサーの回路問題が苦手です・・・どう解いていけばいいのかわからないんです
リケジョ志望のAIさん
高校物理の電磁気分野で圧倒的に頻出なのは「回路問題」です。中でもコンデンサーの問題の中でコンデンサーの扱いに戸惑う人も多くいます。
今回は、合成容量とか一切使わずにたった2ステップでコンデンサーのある回路問題を解く方法をお見せしましょう！必見です！
↓コンデンサーについて基礎を学びたい人はこちらをチェックしてくださいね↓
【物理】コンデンサーの公式ってどう導く？コンデンサーの性質大公開！
・コンデンサーの問題が楽々解けるようになる
・たった2ステップで解くことができる
目次
コンデンサーの問題でやるべき２つステップとは？
その2ステップがすごく気になります！！教えてください！！
AI
もちろん教えるよ！それがこれです！！
AKINORI
- 島（独立部分）を見つける→「電荷保存則」
- 電位差マークをつける→「一周した電位＝０」
何ともシンプルですよね
本当にこれだけでコンデンサーの問題（というより回路問題全般）を解くことができます。
それを今から例題と一緒に見ていきましょう！！
図のように電気容量がそれぞれ\(C_1, C_2, C_3\)のコンデンサーがあり、起電力\(V\)の電源がつながれている。各コンデンサーに蓄えられる電気量を求めよ。なお、コンデンサーは初めは電荷が貯まっていないものとする。
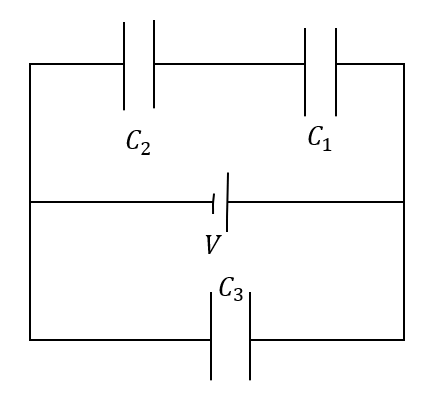
コンデンサーの問題解法１：電気量保存則
最初のステップとしてこれをやります。
島（独立部分）を見つける！
図を見せた方が早いと思いますので、これを見てください。
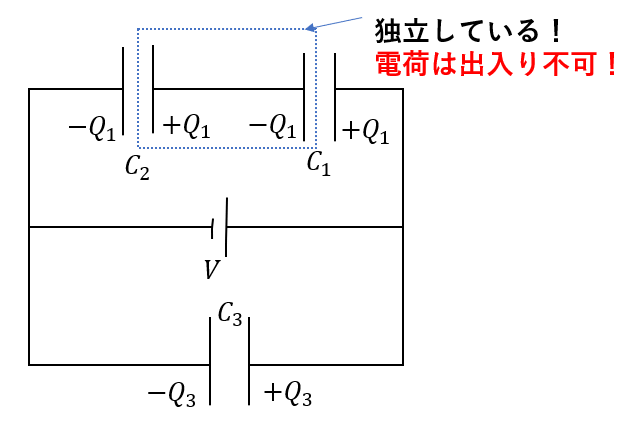
コンデンサー\(C_1, C_2\)の内側（破線部分）は導線で繋がっておらず、完全に孤立しています。
つまり島です。ぼっちです。
コンデンサーは極板が向かい合う構造をしているので、どうしても孤立する「島」ができるんですね。
この島を見つけることが非常に重要になってきます。その理由は
電荷が出入りがない
からです！！
つまり、プラスマイナスを含めこの島での総電荷量は
一定
となります。
これをカッコよく電荷保存則と言ったりします。
これはマジで重要なので理解をしておいてください。
AKINORI
今回の場合、島では最初電荷はたまっていなかったので０です。
そして、充電後は両極板に電荷が現れますが、これらはプラスマイナス含めて足したら０になっていないといけませんね。
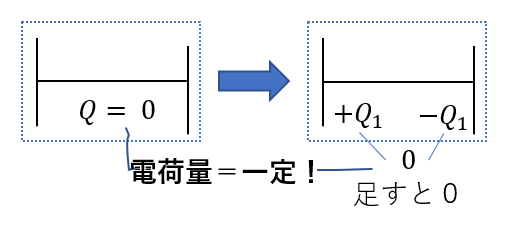
ということで、図のように
符号が違うだけで、大きさは同じ電荷が極板に現れるのです！！
なるほど、これを使うと必要な文字が一個減るんですね。「島」を見つける、理解しました！
AI
これが最初のステップ今度はここで考えた電荷量から、電位差の関係を見ていくよ！
AKINORI
コンデンサーの問題解法２：キルヒホッフの法則
次のステップとして、さっき考えた電荷量をもとに、電位差を見ていきます。
ここでポイントです。
回路中で電位差が生じているところにマークをしていきましょう！
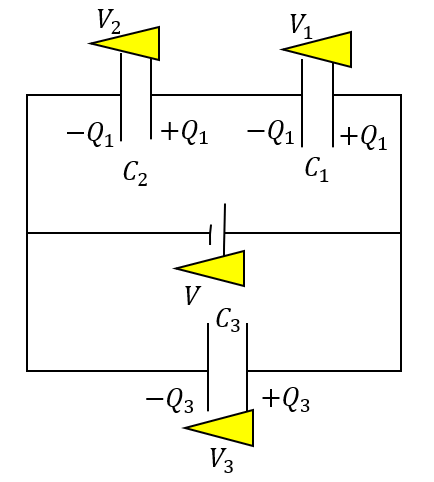
マークの付け方はなんでもいいですが、僕はこのように三角形のマークをつけています。
こう書くことで
三角形が広がるほうに電位は上がっていく
というのがはっきりするのでいいかなと思います。
電圧マークが書けたら、キルヒホッフの法則を使います。
キルヒホッフの法則については別の記事で説明しますが、簡単に言うと
「一周した電位＝０」です。
例えば図のように回路を一周してみます。
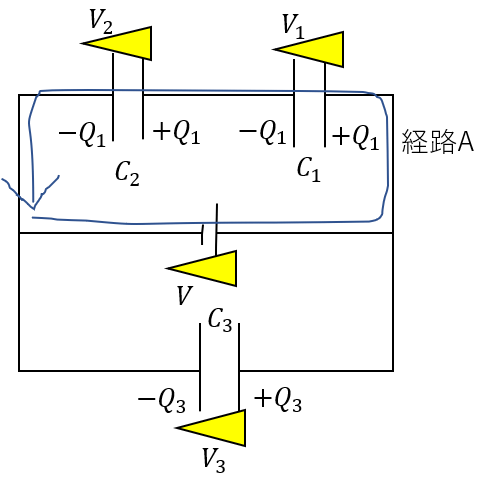
イメージとしてはデパートです。
1階のレストランから出発して最終的にこのレストランに戻ろうとすると
2,3階・・・と何階でも上がろうと、同じだけ下りなければ戻れませんよね。
それと同じです。
もとの電位に戻るには、電位が上がった分、下がる必要がありますね。
電位が上がる（三角形が広がる）向きならプラス
電位が下がる（三角形が狭まる）向きならマイナス
として、各電位を足していくと、必ず０になるのです。
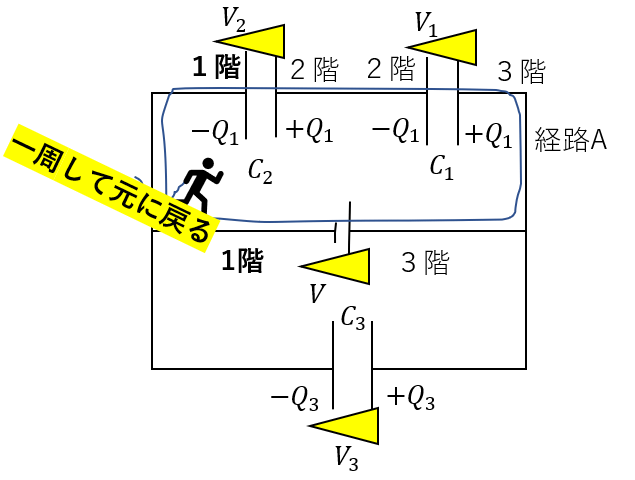
電源：三角形の大きくなる向きなのでプラス（\(+V\)）
コンデンサー\(C_1\)：三角形の狭まる向きなのでマイナス（\(-V_1\)）
コンデンサーは\(C_2\)：三角形の狭まる向きなのでマイナス（\(-V_2\)）
これらを足してそれが0になるのでこうなります。
\(V – V_1 – V_2 = 0\)
進む向きによってプラスマイナスがかわるので、
どういう向きに一周するかもしっかり図示しておくといいでしょう。（図のように矢印をかいてください）
なるほど！この一周する経路ってどんな経路でも良いんですか？
AI
もちろん！ただ、一筆書きで一周できるようにしてね。
AKINORI
別の経路も考えてみましょう。
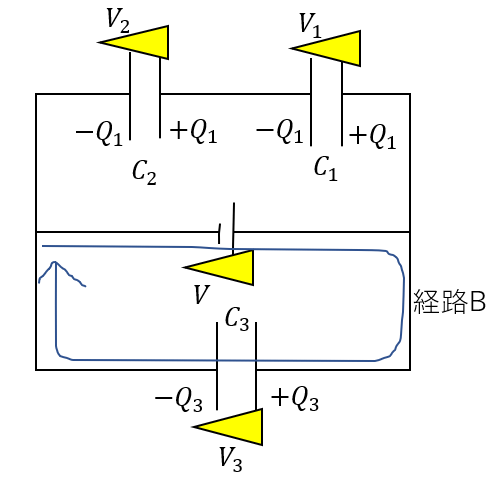
これも同じようにして
\(V – V_3 = 0\)
となります。
なるほど！意外と簡単ですね！
AI
そう！意識することはたった二つだし、やることもそんなに難しくないから方針が立てやすくていいね。
AKINORI
ここまで来たら後は楽勝です。
\(V – V_1 – V_2 = 0\)
\(V – V_3 = 0\)
この二式と、コンデンサーの重要公式である
\(Q = CV\)
を使えば電荷量は求まります。
一つ目の式を変形すると
\(V – \frac{Q_1}{C_1} – \frac{Q_1}{C_2} = 0\)
\(Q_1 = \frac{C_1 C_2}{C_1 + C_2}V\)
となります。
また、二つ目の式も同様にして
\(Q_3 = C_3 V\)
となりますね。
電荷量はどう定めればいいの？
ちょっと待ってください！最初の電荷ってどう定めればいいですか？さっきは何の迷いもなく電荷量を設定していましたけど・・・
AI
実は、電荷量の決め方、つまり符号は適当でいいんだ。答えは結局同じになるからね。
AKINORI
さっき、コンデンサーの電荷量を定義する際にこうしていましたね。
でも、この電荷の符号は適当につけてOKです。その分\(Q_1\)の答えがマイナスになるので「あ、逆だったんだな」と結果的にわかります。
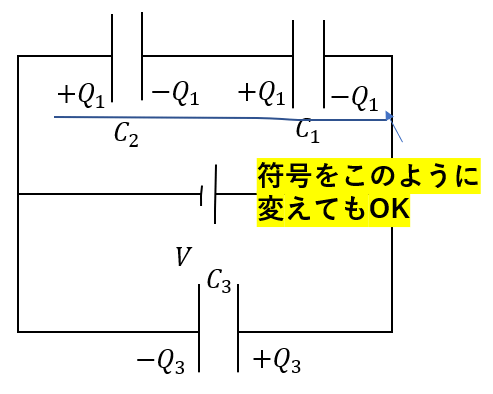
ただし、一回決めたら答えを出すまでは符号を変えないでくださいね。
電位差マークもこの設定した電荷で考える必要がありますので注意してください。
「負→正」で大きくなるように書いてくださいね。
あまりマイナスとか出るのは嫌なので、なるべく予想して電荷量を決めておくといいですね。
例えば電源の正極側にある極板はプラスに帯電くらいは予想つきますよね。
なるほどです！答えがマイナスになるかプラスになるかの違いで結局一緒なんですね！
AI
そういうこと。今日学んだことは入試問題でも絶対必要なテクニックなのでしっかり復習してね！！
AKINORI
スイッチがある場合はどうしたらいいの？
今回の問題は基礎の基礎問題です。入試問題では間違いなくスイッチ操作が絡んできます。
スイッチを閉じた直後、十分に時間が経過するとコンデンサーはどうなるのか？
そのあたりはこちらで説明しているので見てくださいね。
まとめ：どんなコンデンサーの問題でもこれを使え！
いかがでしたか？
今回の回路は比較的簡単だったと思うし、中には合成容量とか使った人もいるかと思います。
ですが、入試問題ではもっと複雑になったりスイッチ操作が加わったりすると混乱しますし、合成容量なんてそもそも使えなくなります。
この方法なら、絶対にどんな問題でも解けるので必ず使えるようにしましょう！
コンデンサー回路で意識すべきたった２つのこと
- 島（独立部分）を見つける→「電荷保存則」
- 電位差マークをつける→「一周した電位＝０」
2週間で入試で勝てる電磁気ノウハウを手に入れ偏差値を10上げるオンライン塾開講中！
