電位と電場の違いって？公式を導出すればわかるで！
電位の式を導出する方法が分かる
電場と電位の違いが分かる
電場と電位というのを学校で習ったんですがイマイチ分からないです。何が違うんですか？
AI
全然違うものだよ。電位っていうのはエネルギーのことです。
AKINORI
ふ～ん（わからん）
AI
まあ、ここでは電位というものを理解して、電位の公式を導いてみましょう！！
AKINORI
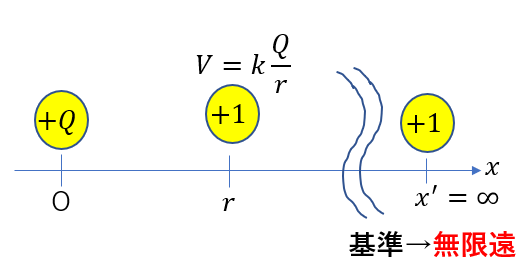
点電荷については電位の式をいきなり紹介される人も多いのでは？
\(V = k\frac{Q}{r}\)
いきなりこういう公式を言われて
「はい、覚えなさい！！」
って先生や、教科書に言われる。
んで、後付けのように電位の説明をさせられる。そんなんじゃ・・・
電場と電位の違いなんて理解できるわけがないです！！
電位のこの公式を導出する過程を理解すれば電位と電場の違いなんて一目瞭然です。
ということで、実際に電位を１から求めてみましょう！！
電位とは？
「電位」は「電場による位置エネルギー」のこと。電場は「力」のようなもので電位はエネルギーです。
AKINORI
あ！電場を考えるってことは、＋１[C]を置いて考えればいいんですね！！
AI
電場についてはこちらを確認しておいてね！
電位はエネルギー。ということは
を使って求めることができそうですね。
電場を考えるときは＋１[C]の電荷を置く。これが鉄則でした。
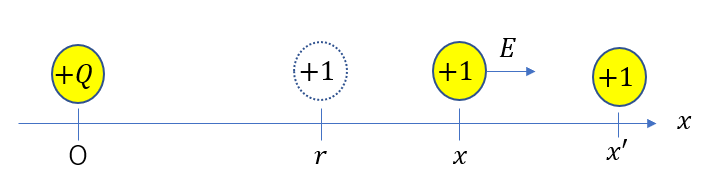
＋１[C]の受ける静電気力が電場になるので距離\(x\)の位置での電場の大きさは
\(E = k\frac{Q\cdot 1}{x^2} = k\frac{Q}{x^2}\)
ですね。
ここで、＋１[C]の電荷を距離\(r\)のところから静かに放すと、図の右向きに動き出しますね。
なのでこの電場は仕事をします。
位置\(x’\)での速さを\(v\)とすれば、エネルギー原理
（はじめの運動エネルギー）＋（された仕事）＝（あとの運動エネルギー）
から
\(0 + W = \frac{1}{2}mv^2\)
ですよね。
右辺はエネルギーです。なので、左辺もエネルギーとして扱ってあげたいわけですよ。
さらに、静電気力っていうのは保存力です。
なので、このエネルギーは特に「位置エネルギー」となります。
つまり、この仕事\(W\)を「電場による位置エネルギー」ということで「電位」と定めましょう！！
ということです。
あとは、この仕事\(W\)を求めるだけですね。
でも、電場って位置によって変化しますよね？「力×距離」で求められませんよね？
AI
そう、だからグラフの面積を使うしかないんだ。
AKINORI
電場の式をよく見ると
\(E = k\frac{Q}{x^2}\)
という風に、位置\(x\)によって大きさが変化しちゃうんですよ。
なので、グラフを書いて面積を求めるしかない。
あれ？でも今回グラフの面積求められないいなじゃいんですか？曲線になっちゃいます。
AI
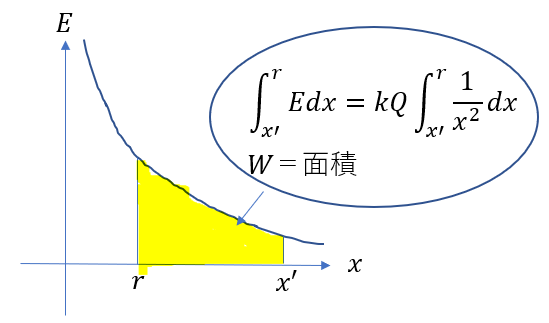
今回E – xグラフを書いて見ると、厄介なことに面積を見た通りには求められないんですよ。
これは積分を使うしかない
\(W = \int_r^{x’} E dx = kQ\int_r^{x’} \frac{1}{x^2} dx\)
これは数Ⅲをやればできる積分です。今回は結果だけ出しますね。
\(W = -\frac{kQ}{x’} + \frac{kQ}{r}\)
私が知ってる電位と比べるとなんか余分な項がありますね。
AI
そうだね。これは位置エネルギーならではの方法で消すことができるよ。
AKINORI
この\(W\)は位置エネルギーです。
位置エネルギーっていうのは基準点を好きに取って良い！
こういう特徴がありました。重力の位置エネルギーを思い出してください。
どこにとっても良いなら、式が簡単になるほうが良いですよね。
簡単にするには
\(\frac{kQ}{x’}\)
を消したいですよね。
これも数Ⅲの話になってしまいますが、これを消すには\(x’ \to \infty\)とすればいいです。
分母をどんどん大きくしていくと、全体の値はどんどん小さくなって０に近づいていきますね。
つまり\(x’ \to \infty\)を考えると０となります。
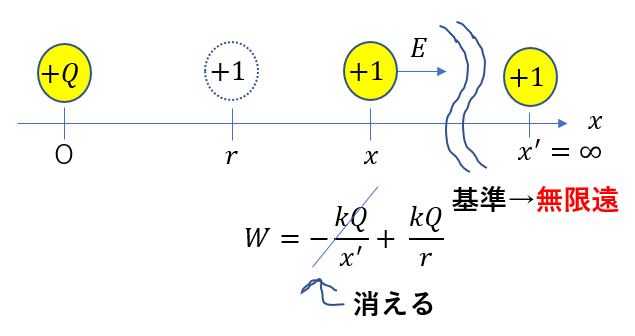
そうすれば、電位\(V\)は
\(V = k\frac{Q}{r}\)
となるわけです。
ただ、この時点で基準点を無限遠に取っているので、基準を変えてはいけません。
そうすると電位の式が変わってしまいます。
なるほどです
AI
高校物理では原則は微積を使わないので、これを覚えるように言われるんですね。僕は覚えるのは否定しないけど、意味を理解した上で覚えてね。
AKINORI
等電位面と電場
最後に、等電位面と電場の関係をお話したいと思います。
電位というのは
\(V = k\frac{Q}{r}\)
見ての通り、距離\(r\)に影響するものです。
さっきは一直線上で考えましたが平面でも同じことです。
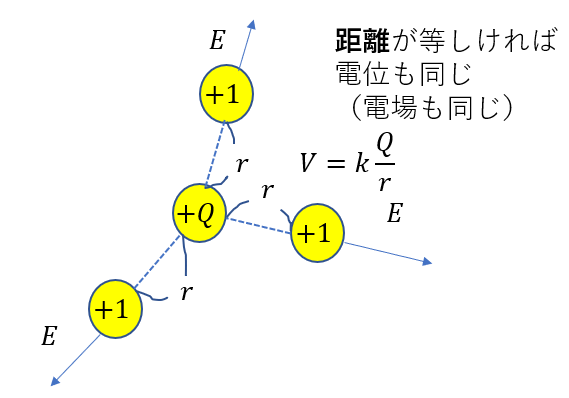
このように、電荷\(Q\)から距離が等しいところを結ぶことができます。
それは円です。
これを「等電位面」と言います。
そして、この円上では電位は変化しない。
つまり、電場は仕事をしません。
ということは、電場はこの線に対して垂直でないといけませんね。
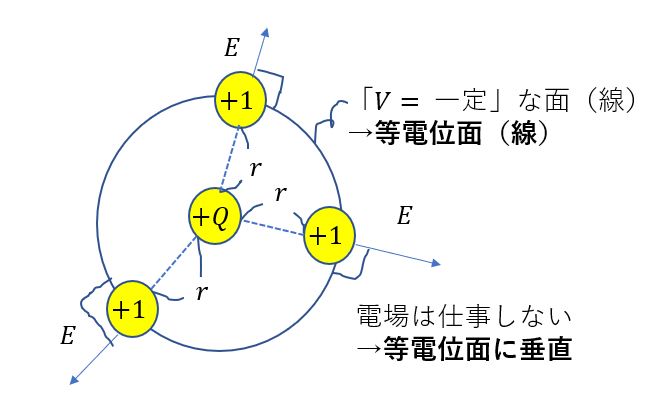
このように、
「等電位面と電場（電気力線）は垂直に交わる」
のです！！
へ～。これって問題で使えるんですか？
AI
正直、そこまで使えない。というより、使う場面がないのよね。ただ、電場と電位の違いというテーマだったので、どういう関係があるのかな？っていうことでこんな話を持ってきました！
AKINORI
まとめ
- 点電荷による電位
距離\(r\)における電位（電場による位置エネルギー）は
\(V = k\frac{Q}{r}\)
＊基準は無限遠
