実効値って?交流回路の抵抗の扱いを超解説!

・交流回路での抵抗の扱い方が分かる
・実効値の意味が分かる
電磁気の問題で圧倒的に多いのが「回路問題」です。じゃあ、回路問題って難しいのかな?って言われるとそんなことありません。
回路問題がきたらガッツポーズしてください。
直流でも交流でもやることは決まっていて
・キルヒホッフの法則
・抵抗、コンデンサ、コイルの性質
この二つを使えば余裕で解けるからです。
直流の回路に関しては別の記事でやっておりますので、ここでは交流について話をしていきます
- 抵抗
- コンデンサー
- コイル
それぞれの回路での性質を見ていきます。今回は抵抗です
コンデンサー、コイルはそれぞれこちらで確認!
交流回路における抵抗
抵抗でもコンデンサーでもコイルでも
交流回路の場合は以下の点について考えます
・電流と電圧の関係
・直流回路への変換
それを踏まえたうえで見ていきましょう。
\(V = V_0\sin{\omega t}\)の交流電源に抵抗\(R\)をつなげる。この時の抵抗の働きについて考えよう
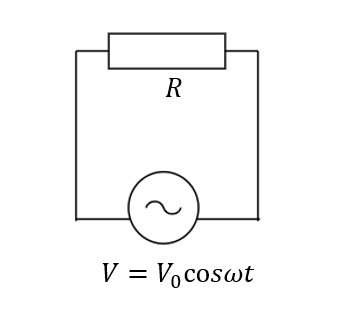
電流はどう表される?
まず、電流について考えます。もちろん回路なのでキルヒホッフの法則ですよね。
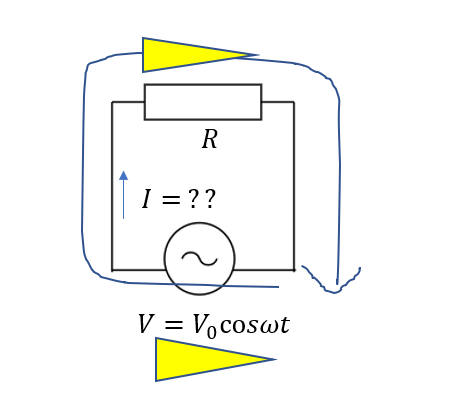
もちろん、交流電源なので起電力の向きや大きさは変化していきますが、ある瞬間の状態を考えれば十分です。
「一周した電位=0」なので、図のように一周すれば
\(V_0\sin{\omega t} – RI = 0\)
\(I = \frac{V_0}{R}\sin{\omega t}\)
\(I_0 = \frac{V_0}{R}\)(電流の最大値)と置けば
\(I = I_0\sin{\omega t}\)
となります。当然ながら電流も時間で変化することが分かりますね。
コイル・コンデンサーとの比較
コンデンサーとコイルとの違いを比べてみます。結論からいうと位相に違い特徴がみられます。
位相とは・・・
図形的に見ると「円運動における物体の角度」
グラフ的に見ると「最大値や最小値を取る時間」
数式的に見ると「sinやcosの中身」
位相って難しいのでとりあえずこのように理解しておいてください。今回は数式的に見ます。
電圧と電流はともに\(\sin{\omega t}\)ということで、sinの中身が一致していますよね。なので抵抗の場合、電圧と電流は同位相ということです。
同位相ということは、ある時間で電圧が最大値を取るなら電流も最大値を取る、電圧が最小値を取るなら電流も最小値をとる、といった具合に変化の仕方が同じということです。
これが抵抗の特徴です。
実効値は直流に見立てるためのもの
交流の分野に入るといきなり「実効値」っていう言葉が出てきます。これって何?と思いますよね。
実効値というのは「交流回路を直流回路に置き換える」ためのものです。日常生活では交流電流が使われています。そのため時間ごとに電流や電圧が変化し、消費電力を求めるのが非常に困難になります。直流回路はそこが楽です。
そのため、うま~く直流回路に置き換えて消費電力を求めよう!
と思ったときに出されたのが実効値ということなのです。
まあ、受験には日常生活なんてどーでもいいと思うので「交流を直流に置き換える」というイメージを持っておいてください、
ということで、抵抗の消費電力を求めます。抵抗の消費電力はこうです。
\(P = IV = I_0V_0\sin^2{\omega t}\)
さきほど言ったように時間で変化するので厄介です。
なので、長い時間をとって平均をとります。
\(\overline{P} = I_0V_0\overline{\sin^2{\omega t}}\)
理系のみなさんなら
\(\sin^2{\theta} = \frac{1-\cos{2\theta}}{2}\)
この公式くらい知ってますよね?
これを使うとこうなります。
\(\overline{P} = I_0V_0\frac{1 – \overline{\cos{2\omega t}}}{2}\)
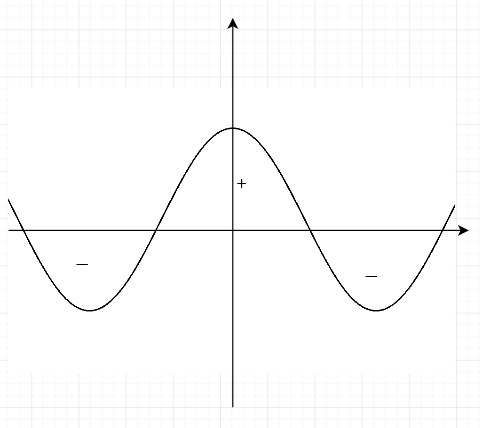
さて\(\cos{2\omega t}\)の平均ですが、このグラフを見ると・・・
プラスの領域とマイナスの領域が交互に並ぶよね。ず~~~~と長い時間を取れば(無限時間とれば)
+-+-+-+-・・・
となって打ち消しあって0になりますね。つまり\(\overline{\cos{2\omega t}} = 0\)です。ということで
\(\overline{P} = \frac{I_0V_0}{2}\)
となります。
そしてこれを直流のように扱いたいんですよね?これは電力なので「\(IV\)(電流×電圧)」っていう形にしたいんです。そこで
\(\overline{P} = \frac{I_0}{\sqrt{2}}・\frac{V_0}{\sqrt{2}}\)
と無理やりしましょう。そして
\(I_e = \frac{I_0}{\sqrt{2}}, V_e = \frac{V_0}{\sqrt{2}}\)
と置いてやれば
\(\overline{P} = I_e V_e\)
\(I_e , V_e\)はそれぞれ定数ですから、見事に直流っぽくみなすことができました。
「交流の電力消費は、直流で\(I_e, V_e\)の電力消費と同じ」まさに「交流→直流」の置き換えです。
交流も直流もやることは同じ
いかがでしたか?
見ての通り、やっていることは「キルヒホッフの法則」だけです。交流だから直流にはない「位相」とか「実効値」という概念は出てきますが、根本は全く同じわけです。
なので、しっかり直流回路の問題が解ければあとは交流の基礎知識を身に付けるだけで回路分野は終わるんです。行ける気がしませんか??
最後にまとめておきます。
・抵抗に流れる電流の位相と電圧の位相は同じ(変化の仕方が同じ)
・実効値は最大値の\(\frac{1}{\sqrt{2}}\)倍(交流→直流の変換)