【重要】キルヒホッフの法則とは!回路問題8割クリアできる解き方とは!?

キルヒホッフの法則の意味が分かる
キルヒホッフの法則の使い方が分かる
回路問題の解き方が分かる
こんにちは!受験物理Set Upです。
今回はですね。電磁気分野で一番大事なこと学んでいきます。そうです!
キルヒホッフの法則
です。
キルヒホッフの法則を制する者は電磁気を制す!
と言っても過言ではありません!(過言です(笑))
キルヒホッフの法則は回路問題で一番の土台に当たるものです。キルヒホッフの法則の理解、その使い方をおろそかにしていると後で痛い目に合います。
間違っても
(起電力の和)=(電圧降下の和)
なんて覚え方しないでくださいね。
キルヒホッフの法則の意味を理解する過程がそのまま問題の解き方につながりますからしっかり学びましょう!
今回は、キルヒホッフの法則の意味はもちろん、
キルヒホッフの法則を使った問題の解き方を分かりやすく教えていきます。
目次
キルヒホッフの法則とは?

キルヒホッフの法則は回路における電流や電位に関する法則です。
キルヒホッフの法則
- 電流は途中で増えたり減ったりしない
- 一周した電位=0
たったこの二つです。特に二つ目の「一周した電位=0」は一生お世話になるので確実に理解してください。
ではこの二つに関して詳しく見ていきましょう!
 AKINORI
AKINORI
電流は途中で増えたり減ったりしない

入試問題では回路問題が出ると、絶対に複雑な形をしています。回路がいろいろ分岐しています。
この分岐点では面倒なことに、電流が入ったり出たりするわけです。
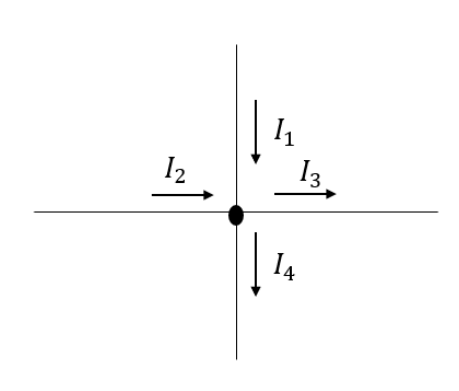
でもこの分岐点で、全体の電流が増えたり減ったりしませんよね?
例えば交差点での車を考えたとき、
- 交差点に向かう車の台数
- 交差点を抜ける車の台数
これが異なるわけないですよね。

合計4台の車が交差点に入れば、合計4台の車が交差点から出てくるわけです。
同じことが電流でも言えます。
- 分岐点に流れ込む電流
- 分岐点から流れ出る電流
これらは等しいんですよ。
ということで、さっきの図では
\(I_1 + I_2 = I_3 + I_4\)
が成り立ちます。
これがキルヒホッフの法則の第一法則です。
「電流は途中で増えたり減ったりしない!」
一周した電位=0

例えばこんな回路があるとします。これには次のように電圧がかかっています。

僕はこのようにマークしていますが、この電圧マークは自分の好きに書いてください。
ただしどっち向きに電位が大きくなるのかははっきり分かるようにしてくださいね。
この回路を一周して元に戻ったとき電位が0に戻る。
これがキルヒホッフの法則の2つ目です。

これはデパートをイメージしてもらえばいいです。
コンデンサーのところでも同じ説明をしているのでそちらをみてください。
回路を回るときに、
電位が大きくなる向きならプラス
電位が小さくなる向きならマイナス
としてそれぞれの電位差を足していったとき0になるということで
\(V_1 – V_2 – V_3 = 0\)
と表すことができます。
よく教科書などでは(起電力の総和)=(電圧降下の総和)
と考えると符号がごちゃごちゃになったり
コンデンサーや電源が2個あるときなどに絶対に混乱するので、今伝えた通りの方法で「一周した電位=0」と考えましょう。
これって交流のときでも使えるんですか?
 AI
AI
もちろんです!
 AKINORI
AKINORI
よく勘違いがあるのですが、これは抵抗のみの直流回路に限った話じゃないです。
交流だろうが、コイルがあろうがコンデンサーがあろうが成り立ちます。
なので回路問題にはこの「一周した電位=0」が強力なのです。
キルヒホッフの法則を使った回路問題の解き方
じゃあ、このキルヒホッフの法則を使って実際に問題を解いてみましょう!
 AKINORI
AKINORI
図のような回路において、各抵抗に流れる電流の大きさと向きを答えよ。
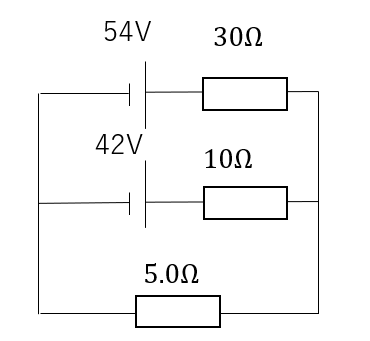
まず電流を定めてキルヒホッフの「電流の法則」を使おう。
電流を求めたいので、まず電流を設定しないといけませんね。向きはなんでもいいのでとりあえず図のように設定しましょう。

こんな感じ。
そして、さっき見たキルヒホッフの法則の電流の法則を使ってそれぞれの電流の関係式を立てます。
例えば分岐点Pを見ると
流れ込む電流=流れ出る電流
なので
\(I_1 = I_2 + I_3\)
となりますね。
電圧マークを書いて「一周した電位=0」
次に「一周した電位=0」を使います。
まず最初に電位差マークを書いていきます。
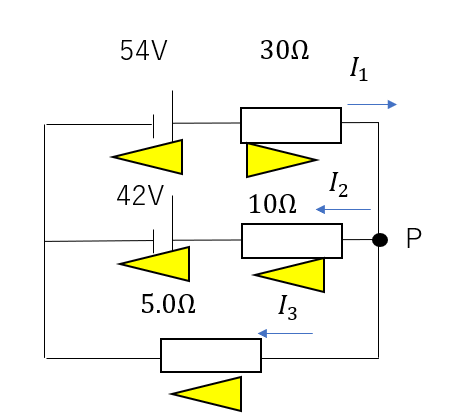
これは絶対にサボらないでやってください。
抵抗にも電圧がかかります。電流が流れる方向に電位が小さくなっていき、その大きさはオームの法則
\(V = RI\)
で求まります。
そしたら、向きも含めて、適当に回路を一周します。
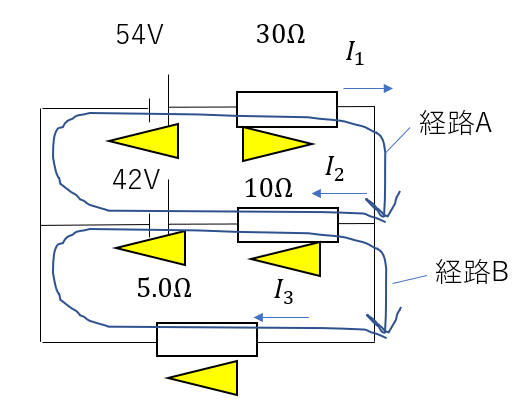
向きも設定しないと「電位のどっち向きに進むのか」が分からなくなってしまうので必ず向きも考慮してください。
今回は二つの経路A,Bを考えてみました。
ではいきます。
- 経路Aについて
\(-10I_2 – 42 + 54 – 30I_1 = 0\)
∴\(15I_1 + 5I_2 = 6\)
- 経路Bについて
\(-5.0I_3 + 42 + 10I_2 = 0\)
∴\(-10I_2 + 5.0I_3 = 42\)
これらとさっき求めた
\(I_1 = I_2 + I_3\)
という関係を使えば
\(I_1 = 1.2 , I_2 = -2.4 , I_3 = 3.6\)
と答えが出ます。
符号が実際の向きを教えてくれる!
あれ?マイナスが\(I_2\)はマイナスが付いてますね?これでいいんですか?
 AI
AI
このマイナスは「最初に自分で定めた向きとは逆に流れるよ!」っていうことを表しているだけなんだ。
 AKINORI
AKINORI

それを踏まえて答えると
- 上の抵抗・・・右向きに1.2A
- 真ん中の抵抗・・・右向きに2.4A
- 下の抵抗・・・左向きに3.6A
答えの符号で最終的な向きがわかるので、最初に設定する電流は好きに決めてOK!ただ、マイナスが出ると面倒なので、なるべくプラスになるように向きは予想して決めておくといいよ!!
 AKINORI
AKINORI
なんか回路問題いけそうな気がします!!
 AI
AI
ちなみに、回路を一周するときは一筆書きで一周できればどんな周り方でも構いません。
また回る向きも好きに決めて構いません。
キルヒホッフの法則で回路問題は楽勝

いかがでしたか?
キルヒホッフの法則は非常に重要な法則です。入試までずっとお世話になります。
回路問題が出たらこれを頻繁に使うことになります。これを使いこなせば回路問題は楽々解けます。
今見せたステップもがっつりマネしてください。
これが一番楽で安定して点数を稼げる解き方です。
- 電流は途中で増えたり減ったりしない(電流の法則)
- 一周した電位=0(電位の法則)








Comment
キルヒホッフの法則は I1+I2+i3=0と閉回路の任意の一点での電位は一つに決まる(接続していれば当然)
で解けます。大学生のころに実験物理の教官に、「等価回路」を解明してみたらといわれていました。
電池と抵抗を直列にして1組とします。これを3組並列に結びます。なんとこれで回路を流れる電流が計算できます。難しい方程式を解かなくて済むのです。つまり、重ね合わせの理やテブナンの法則は必要なくなります。
キンドル本で「キルヒホッフの法則と実験」を書きました。
連立方程式の解き方では計算が大変です。拙著『キルヒホッフの法則と実験』を参考にしてください。連立方程式をとかなくてすみます。中学生でも解けると思います。電子本のKindleで99円です。
電流の向きは「なんでもいい」とありますが、適当に決めたらI1=I2+I3を使えなくなりませんか?
第二法則について
色々なサイトや本を見ても、どうもしっくりこなかったのですが、こちらの解法だと良く分かりました。
まず、とにかく各回路に流れる電流の向きを決めて、各抵抗に三角形をつける。
電源は、電流の向き関係なく、マイナス側に三角形の先端がくる。
あとは、右回りもしくは左回りで、式を作る。
来週の資格試験に間に合いそうです。
ありがとうございました!
簡単な解き方はあります。拙著電子本「キルヒホッフの法則と実験」です。高校生のために¥99としました。
第一法則を 電流の代数和=0とし、第二法則を 電圧ではなく電位で書きます。すると0でない電位か求まりますから、電流値を求めることができます。これを基本に 重ね合わせの理とテブナンの法則が理解できます。
ありがとうございます。おそらくその表現の方がより厳密かもしれません。
あくまで高校物理なので、ここではあまり難しく考えず、図にして見た通りに理解できるようにしています。
やっと解くことが出来ました。
こんなことを何度も質問していたと思うと恥ずかしいです。
ありがとうございました‼️
私にはやっぱり解けませんでした。
これ以上、ご迷惑をおかけすることは出来ませんので、諦めます。
ありがとうございました。
I 1 =I 2 +I 3 なので、15I 1 +5.0I 2 =6のI 1のところに、I 2、I 3にあたる−10I 2 +5.0I 3 を代入しました。
この考え方が間違っているということでしょうか?
ますます分かりません。
違います。同じことの繰り返しですが、
\(15I_1 + 5I_2 = 6\)
\(-10I_2 + 5.0I_3 = 42\)
\(I_1 = I_2 + I_3\)
この連立方程式を解くだけです。
アドバイスありがとうございます。
せっかっくヒントを与えていただいたのに、やっぱりわかりません。
15I 1 +5I 2 =6のI 1の部分に−10I 2 +5.0I 3 を代入し、
−10I 2 +5.0I 3 =42 との連立方程式を解くと、I 2が−124.8とかという数字になってしまいます。
そのまま続けていくと、I 3が 241.2、I 1が42になってしまいます。
私の頭ではこれが限界です。何度もすみませんが、教えてください。
「\(15I_1 + 5.0I_2 = 6\)の\(I_1\)の部分に\(-10I_2 + 5.0I_3\)を代入し」の部分がよくわかりません。それはどこから来てますか?
先ほど申し上げたように、1つずつ文字を消去して(代入などして)いけば解けます。
早速の回答ありがとうございます。
符号の付け方につきましては、理解できました。
ありがとうございます。
計算ですが、何時間も考えておりますが、文字が違うため、どのようにして解くのか分かりません。
I 1 =I 2 +I 3を利用して、色々な形に変えて計算してみましたが、分かりません。
教えていただけないでしょうか?
よろしくお願いいたします。
代入して文字を1つずつ消去していけば解けると思いますよ。
例えば\(I_1 = I_2 + I_3\)と\(15I_1 + 5I_2 = 6\)で\(I_1\)を消去するなどすれば解けます
はじめまして。
教えてください。
経路A −10I 2 –42+54–30I 1 =0
経路B −5.0I 3 +42+10I 2 =0
とありますが、符号の付け方の考え方が分かりません。
また、I 1 =I 2 +I 3 という関係を使って計算するとありますが、
どのうようにして計算して答えを出すのかが分かりません。
教えていただけないでしょうか?
よろしくお願いいたします。
符号に関してはこの記事の「キルヒホッフの法則とは」の「一周した電位=0」に書いてあるのでもう一度読んでください。
また計算については、単純な連立方程式で解けます。練習として自力でやってみましょう。