電場って結局何?静電気力と電場の意味をわかりやすく説明します

静電気力と電場の正体が分かる
静電気力と電場の違い・関係がわかる
どうも。受験物理Set Upです。
電磁気分野でまず最初にやるのが、静電気力と電場だと思います。
静電気力は式を覚えるだけで終わるのでここで悩む人は少ないのですが、問題は電場です。
いきなり電場っていう概念が出てきてさっそく混乱する方が続出するのです。
電場って静電気力と何が違うんですか?そもそも電場って何ですか?もう分かりません!!
 AI
AI
こういう質問が多く届きます。
そこで今回は
静電気力と電場の概念について分かりやすく説明していきながら
どういう違いがあってどういう関係があるのか
お話していきたいと思います。
目次
静電気力は暗記してください

まずは静電気力について知りましょう。
電気にはプラスとマイナスがあるのは知ってますよね。
同符号なら反発。異符号なら引き合う。
という具合にお互いに力を及ぼしあいます。
静電気力は実は式として出すことができます。
静電気力の大きさ
\(F = k\frac{q_1q_2}{r^2}\)
\((k : 定数, q_1,q_2 : 電荷量 , r : 電荷間の距離)\)
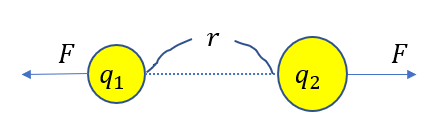
電荷量が同符号なら反発
異符号なら引き合う
ような力が働きます。
あれ?Akinoriさんはいつも導出してくれるのに今回はなしですか?
 AI
AI
実はこれは導出できない式なんだ。ごめん、これ暗記です!
 AKINORI
AKINORI
これはクーロンという方が実験的に導いた式で、導出なんて無いんです。
なので、式は暗記してください。
静電気力に関してはこれでおしまいです。
電場は「遠隔力→接触力」と考えるために生まれた

では今回のトピックであります。「電場」についてお話していきます。
静電気力というのはいわゆる「遠隔力」ですね。重力と同じように、離れている物体にも働く力です。
これに対して接触しているときに生じる力が「接触力(近接力)」と言います。
遠隔力は重力(万有引力)、静電気力、磁気力ありません。ほとんどが接触力です。
この遠隔力ですが、ちょっと疑問に思いませんか?
接触力はイメージ付きやすいけど、遠隔力ってどうなんだろ?離れていても力が生じるっていうのは信じられないな・・・
 AI
AI
ドラゴンボールじゃあるまいし、気で吹っ飛ばすなんてことできないですよね?(笑)
触れている物体にじゃないと力は働かないと考えるのが普通ですよね?
やっぱり偉大な物理学者たちも同じように考えていたわけですよ。
静電気力もなんか接触力のようにとらえたい!そっちの方がイメージしやすいし都合がいい!
 AKINORI
AKINORI
そこで生まれた概念がまさに「電場」なんです。
この電場によって静電気力を「遠隔力→接触力」にみなすことに成功したのです。
電場は「静電気力を及ぼす場」

どうやって静電気力を接触力と考えたかというと・・・
まず、ある電荷を置いたらそこには「電気的な場」ができると考えました。
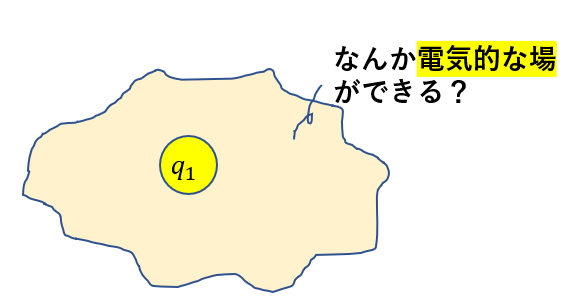
そして、この「場」に別の電荷を置くとその「場」によって力を受けると考えたのです。
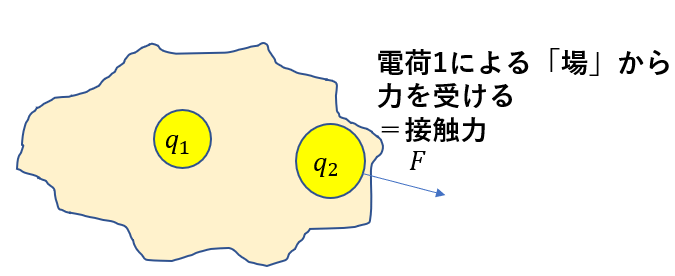
この「場」から受ける力を「静電気力」とし、この「場」を「電場」としたのです。
最初に示した場合だと
「電荷1が電荷2に力を及ぼした」という「遠隔力」の解釈になってしまいますが
このように電場を考えることで
「電場が電荷に接触して力が生じる」というふうに
静電気力を接触力とみなすことができるのです。これが電場の根本の概念になります。
電場はあくまで「静電気力を及ぼす場」であり、静電気力とは全くの別物なんです。
電場を式に表そう

ただ、物理は式にして初めて意味があります。式にしないと使いようがないし、何も発展しないわけです。
そこで電場を式に表してみましょう。
電場はベクトルである
一つ疑問に思ったんですが、その「場」っていうのは電荷を置いた瞬間にできるものなんですか?
 AI
AI
いい質問だね。実はそうではないんだ。この電場の広がり方を深く考えることで電場を式に表すことができるんだ
 AKINORI
AKINORI
電荷を置いた瞬間に電場が全体に広がるということはありません。
池に小石を投げ込んだ時の波と同じように広がっていきます。

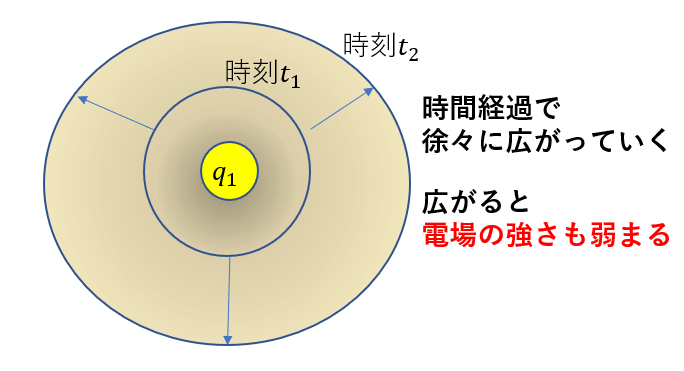
小石を池に投げ入れると、中心から円形にだんだんと外側に広がっていきますよね?
そして外に広がるごとに波の勢いは弱まっていきます。
電場でも全く同じ性質を持っています
このように解釈することで次のようなことが言えます。
- 電場は時間経過で広がる→向きがある
- 電場は離れるほど弱くなる→大きさがある
向きがあって大きさがある・・・ベクトルってことですね
 AI
AI
ということで電場はベクトルなんですね。
ベクトルとなれば力学でもやったように軸を取ってプラスマイナスを考慮したり、分解することができるということです。
電場の大きさは?
ここまで来たら後は大きさを式にできれば良いですね。これはある程度予想がつきます。
電場はあくまで「静電気力」を生じさせるものです。なので、大きさもやっぱり「静電気力」の大きさと似てないと気持ちが悪いですよね。
また、電場は「ある電荷を置いたときに生じる」ものです。
静電気力は、電荷量がそれぞれ\(q_1, q_2\)の電荷があればその両方に影響されました。
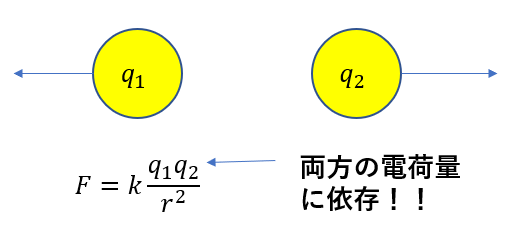
ですが
電場は、置いた電荷の電荷量にのみ影響されるべきです。置いた電荷が作るものですからね。
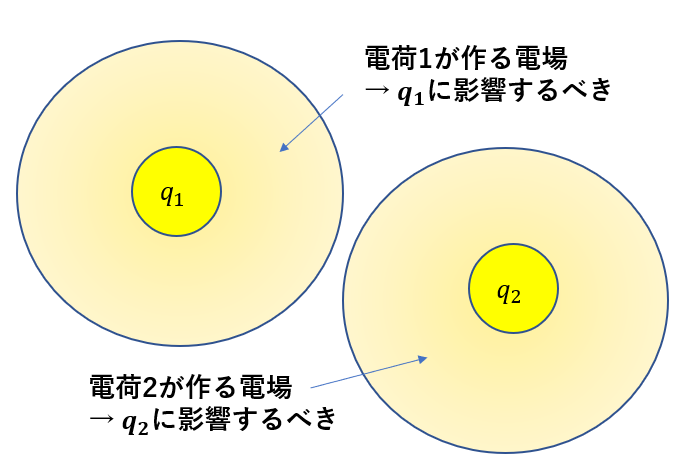
静電気力の式の形を崩さず
置いた電荷にのみ影響する
これらをまとめると、電場の大きさ\(E\)はこのように表すことができます。
電荷量\(q_1\)の電荷が作る電場の大きさ
\(E = k\frac{q_1}{r^2}\)
\(r^2\)が分母に来ているから、遠くなるほど大きさが小さくなるということも現れていますね。
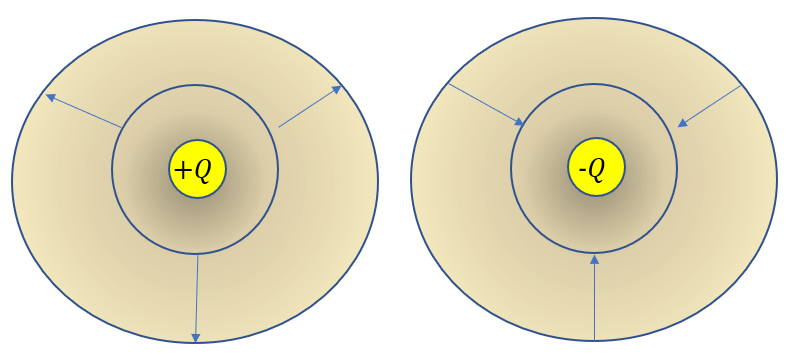
向きに関しては先ほど示した通り、電場は中心から広がっていきます。
- 電荷が正・・・電荷を中心に広がっていく
- 電荷が負・・・電荷に向かって入り込む
電荷の正負で向きは変わります。
静電気力と電場の関係も楽々分かる!

最後に静電気力と電場の式を見比べてみましょう。
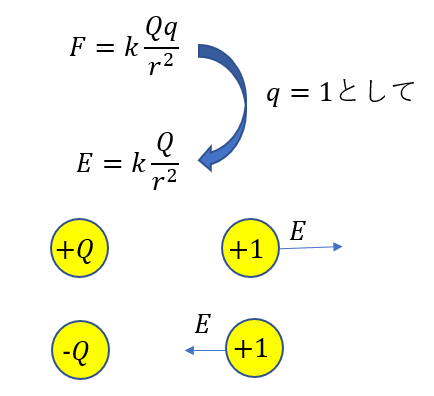
これを見て分かるように
+1[C]の電荷の静電気力が電場
と考えることができます(形式的に)。
ここまで話をしてきましたが、電場はぶっちゃけ分かりにくいですよね。イメージがしにくいです。
ですが、
+1[C]の電荷の静電気力が電場
ということを使えば、問題などで実際に電場を考える際にはとりあえず+1[C]の電荷を置いて考えれば良いんです。
これは非常に大事なので頭に入れておいてくださいね。
深く知れると面白い!

いかがでしたか?
「電場がそもそも何者?」というところが分かったので良かったです。教科書などにはこういう説明がなかったのでためになります。
 AI
AI
もちろん、問題を解く際には電場の式さえ知っていればいいんです。
ですが、せっかく勉強しているなら根本を理解しておいた方が良いですよね。深く知っておくことで損することは絶対ないので、今回学んだ電場の話も一つ、あなたの知識として身に付けておいてください。
- 電場とは
「静電気力」を及ぼす「電気的な場」→ 接触力
・大きさ
\(E = k\frac{Q}{r^2}\)
・向き
正電荷・・・電荷を中心に広がる向き
負電荷・・・電荷に向かって入り込む向き
*電場を知るには+1[C]の電荷を置け!!