電気振動を分かりやすく教えます!コンデンサー2つあるときだって楽勝

こんにちは!オンライン塾を運営している、あっきーです
 あっきー
あっきー
電気振動の原理が理解できない
図・グラフ・式のそれぞれで理解したい
電気振動のエネルギー保存が分からない
コンデンサー2つあるときの対処法が分からない
 リケジョになりたいAIさん
リケジョになりたいAIさん
このような悩みはありませんか?
電気振動は授業の最後の方で扱われるため説明を省かれることが多いです。
ですが、電気振動の問題は出ますし、「コンデンサーが2つある電気振動の固有振動数を求める」という問題も出たりします。
電気振動が解けない理由はいたって単純で、授業で省かれるせいで理解が追い付いていないからです。
この記事では、電気振動の原理を分かりやすく教えるとともに、問題で必要となるポイントもすべて明かします。
最後まで読むことで、以下のことが得られますよ。
電気振動の原理が理解できる
電気振動のグラフ・式のポイントをつかめる
コンデンサーが2つあるときなど、イレギュラーなものも対処できる
電気振動の応用問題も解けるようになる
目次
電気振動とは?

電気振動というのは電気回路において次のように回路をつないだものです。
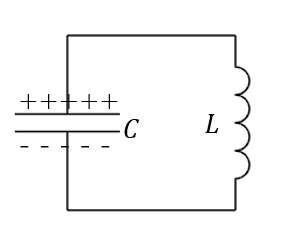
コンデンサーとコイルを並列につなぐことでコンデンサーの電荷が行って返ってという振動が起こります。
この電気振動を図・グラフ・式でそれぞれ見ていきたいと思います。
電気振動では電流が周期的に流れる

\(t = 0\)
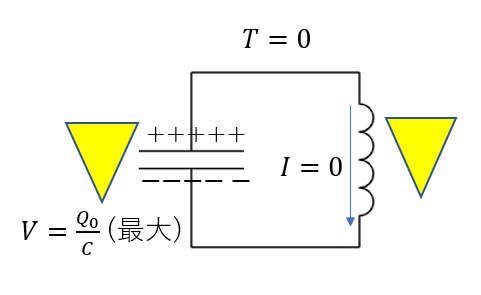
コンデンサーに最大の電荷が貯まっている状態を\(t=0\)として、時間的にどんな変化が起こるか見ていきます。
電荷の蓄えられたコンデンサーは電池と同じ役割を果たすので、本来なら電流が一気に流れ出るわけですが、この場合はそうではありません。
電流が流れ出る瞬間、コイルには誘導起電力が発生します。その電流を押さえようとしてはたらきます。
ですから、いきなり電流が流れ出ることは無く、\(t=0\)では電流は0となります。
一方で、電荷の移動がないのでコンデンサーの電圧は最大の値をとります。
\(t = \frac{1}{8}T\)
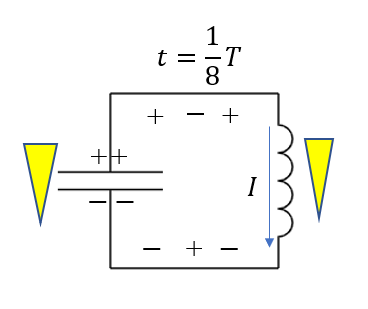
次に時間が経って\(t = \frac{1}{8}T (T:周期)\)となると、電流が流れだします。
図のように下向きに電流が流れ、これを妨げようと誘導起電力が上向きに生じます。
\(t=0\)のときはコンデンサーに最大の電荷が貯まっていたので、急激に電流を流そうとするので、誘導起電力も最大になりました。
しかし、この状態では先ほどと比べて、電流の変化が小さくなるので、誘導起電力の大きさは小さくなります。
\(t = \frac{2}{8}T\)
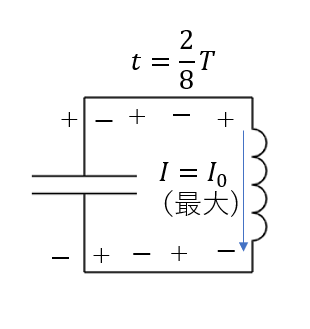
この状況では、コンデンサーの電荷が一瞬0になります。ですから、電流の変化が一瞬なくなり、コイルの誘導起電力も0になります。
今まで、誘導起電力によって電流が妨げられていたわけですがそれがなくなったのです。
つまりこの状況では電流が最大となります。
\(t = \frac{3}{8}T\)

ここまでくると、コンデンサ―の極板に蓄えられる電荷が逆になってきます。最初は上の正、下に負だったのが逆転していますね。なのでコンデンサ―の電圧も向きが変わります。
また、先ほどまではコイルに対して下向きの電流が増えていましたが、この辺りから徐々に小さくなってきます。
するとコイルは下向きの電流を増やそうとするため、誘導起電力も下向きに発生します。
\(t = \frac{4}{8}T\)
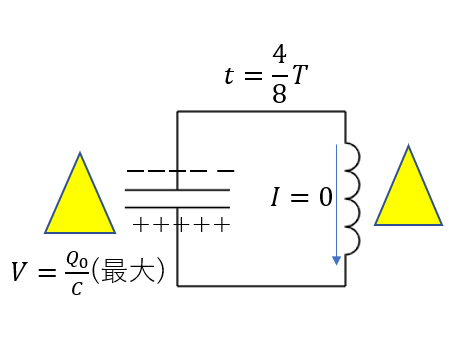
周期の半分過ぎると、\(t=0\)と真逆の状態になります。
コンデンサ―に蓄えられた電荷が逆転し、すぐに電流を流そうとします。
ですが、急激に流そうとすると大きな誘導起電力が発生し、電流はいきなり流れることはなく\(I=0\)となります。
このときの、コンデンサーの電圧と誘導起電力は最大で\(V = \frac{Q_0}{C}\)となります。
これ以降はここまでの状況とすべて逆になります。
\(t = \frac{5}{8}T\)
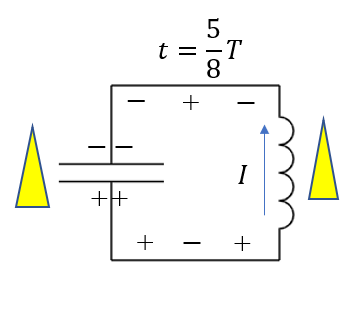
この状態では電流が流れだします。図のように上向きに電流が流れ、これを妨げようと誘導起電力が下向きに生じます。
\(t=\frac{4}{8}T\)のときはコンデンサーに最大の電荷が貯まっていたので、急激に電流を流そうとするので、誘導起電力も最大になりました。
しかし、この状態では先ほどと比べて、電流の変化が小さくなるので、誘導起電力は小さくなります。
\(t = \frac{6}{8}T\)
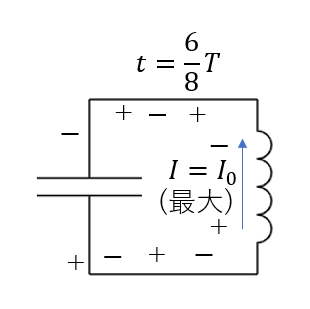
この状況では、コンデンサーの電荷が一瞬0になります。ですから、電流の変化が一瞬なくなり、コイルの誘導起電力も0になります。
今まで、誘導起電力によって電流が妨げられていたわけですがそれがなくなったのです。
つまりこの状況では電流が最大となります。
\(t = \frac{7}{8}T\)
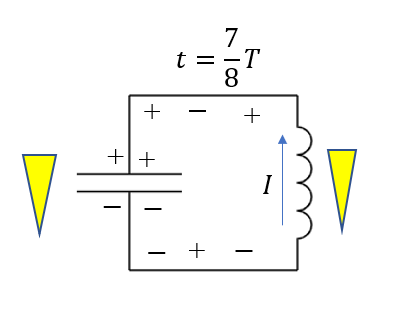
ここまでくると、コンデンサ―の極板に蓄えられる電荷が逆になってきます。下に正、上に負だったのが逆転していますね。なのでコンデンサ―の電圧も向きが変わります。
また、先ほどまではコイルに対して上向きの電流が増えていましたが、この辺りから徐々に小さくなってきます。
するとコイルは上向きの電流を増やそうとするため、誘導起電力も上向きに発生します。
\(t = \frac{8}{8}T\)
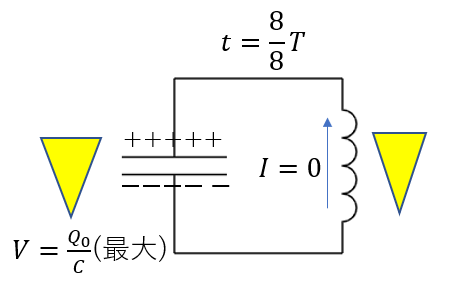
一周して、\(t=0\)と同じ状況に戻りました。
これが何度も繰り返されていきます。これが電気振動です。
*現実には、コイルや導線にも抵抗があるんで、その抵抗によりだんだん電流が小さくなっていきます。そのためどこかでこの振動はストップします。振動がだんだん弱くなる現象を減衰振動と呼びます。
電気振動をグラフにしてみると?

図を使ってイメージができましたね。これをグラフにまとめてみましょう。
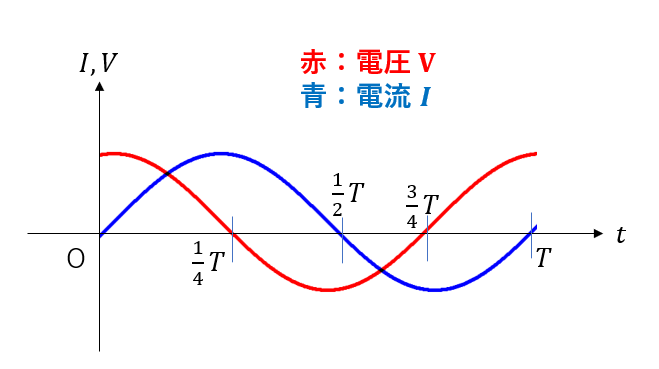
電圧は下から上向きを正に、電流は時計回りを正としています。
例えば\(t = 0\)では、電圧が最大で電流が0ですね。これは図で見せた通りです。
余談ですが、電流と電圧の位相は\(\frac{\pi}{2}\)ずれていますね。
電気振動は共振回路と同じ

図・グラフで説明ができたので、次は式で特徴をとらえましょう。
この回路の周期\(T\)を考えてみます。
あれ?この回路の形って交流の共振回路と同じじゃありません?
 リケジョになりたいAIさん
リケジョになりたいAIさん
お!よく気づいたね。
 あっきー
あっきー
実は電気振動の回路は交流で出てきた並列共振回路と全く同じ形になっています。
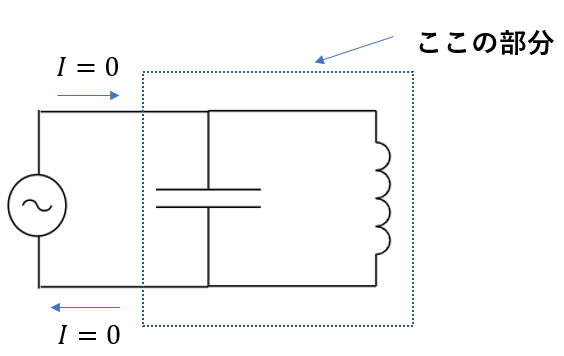
交流のLC並列回路はこのような形の回路です。
そして共振並列回路というのは図のように、電源の電流が0になって点線で囲った回路のみで電流が流れる場合を表します。
点線で囲った部分で電流が流れるというのは、まさにここまで説明した通り電気振動ですよね。
電気振動は共振並列回路と同じなのです。
この共振回路の角振動数は
\(\omega = \frac{1}{\sqrt{LC}}\)
と表せます。
したがって、周期は次のように表せます。
\(T = \frac{2\pi}{\omega} = 2\pi \sqrt{LC}\)
基本的に振動数を使うことが多いので、振動数でも表しておきましょう。
\(f = \frac{1}{2\pi \sqrt{LC}}\)
この振動数は共振回路と同じ固有振動数と呼びます。
ここでは共振回路に関しては詳しく説明しないので、共振回路についてより詳しく知りたい方はこちらを見てください
電気振動のエネルギー保存

もう一つ、電気振動には大きな特徴があります。
それはエネルギー保存です。
最初に電荷を蓄えているのでコンデンサーはエネルギーを持っていますね。
その後電荷が流れてコンデンサーのエネルギーは小さくなってしまいますが、その分コイルのエネルギーが増加します。
このように、コンデンサーとコイルのエネルギーは全体で常に一定に保たれますね。
(静電エネルギー)+(コイルのエネルギー)=一定
はじめ\(Q_0\)の電荷がコンデンサーにたまっていて、ある時間でコンデンサーの電荷が\(Q\)、電流が\(I\)のとき次のように式を表せるわけです。
\(\frac{Q_0^2}{2C} = \frac{1}{2}LI^2 + \frac{Q^2}{2C}\)
*ここで証明しますので、興味のある人だけ読んでください

このグラフから\(V = V_0\cos{\omega t}\)。
\(Q = CV\)より
\(Q = CV_0\cos{\omega t} = Q_0\cos{\omega t}\)
よって、コンデンサーのエネルギー\(U_C\)は
\(U_C = \frac{Q^2}{2C} = \frac{Q_0^2}{2C}\cos^2{\omega t}\)
同じようにグラフから\(I = I_0\sin{\omega t}\)。
\(I = \frac{dQ}{dt}\)、つまり\(Q\)を\(t\)で微分したら\(I\)になるので
\(I = – Q_0\omega \sin{\omega t}\)。
つまり、\(I_0 = -Q_0\omega\)
よってコイルのエネルギー\(U_L\)は
\(U_L = \frac{1}{2}LI^2 = \frac{1}{2}LI_0^2 \sin^2{\omega t}\)
\(= \frac{Q_0^2}{2}L\omega^2 \sin^2{\omega t}\)
先ほどの\(\omega\)を使うと次のように表せる。
\(U_L = \frac{Q_0^2}{2C}\sin^2{\omega t}\)
よって
\(U_C + U_L = \frac{Q_0^2}{2C}(\sin^2{\omega t} + \cos^2{\omega t})\)
\(U_C + U_L = \frac{Q_0^2}{2C}\)
コンデンサーが2つある場合はどうなるの?

電気振動の問題でイレギュラーな問題が出ることもあります。
その一つの例に「コンデンサーが2つある場合の電気振動」が問われることもあります。
横浜国立大学の2009年入試に出たこともあります。
やることは一緒なのですが、別の記事で説明します。
まとめ:電気振動も理解しよう

いかがでしたか?
電気振動はどうしても最後の方に習う単元なので、授業でも簡単な説明だけで終わってしまって理解が追い付かないことが多いと思います。
ですが、入試問題の範囲にもちろん含まれます。
交流回路を苦手にする受験生は多いのでしっかり理解しておきましょう。