共振回路とは？RLC並列回路について分かりやすく解説

2019年10月14日

WRITER

あっきー

　

この記事を書いている人 - WRITER -

あっきー

オンライン物理塾長あっきー。高3秋から1か月で40点点上げ、センター試験では満点を取り、その経験を活かし塾講師として活躍。塾・学校・参考書の内容やカリキュラムに違和感を感じ数多くの高校生を救うため、大学2年生で「受験物理Set Up」を開設。多くの高校生が活用するサイトに発展し、現在「合格への道」で勉強法に特化した受験サポートを行う。

共振回路、RLC並列回路やRLC直列回路。これらに苦しんでいませんか？

共振回路の意味を授業ですっ飛ばすことも少なくありません。

ですが、この共振回路やRLC並列回路・直列回路ってとても大事です。

そして、超簡単に理解することができます。

というのも実生活でも欠かせないのがこの共振回路だからです。

今回の記事では、RLC回路と共振回路の説明と、入試問題ではどのようなことを聞かれるか分かりやすく説明します。

共振回路とは？

まず、共振回路とは何者なのかざっくり説明します。

そもそも「共振」という言葉を知っていますか？

例えばブランコです。

ブランコはタイミングよく後ろから押すことで大きく揺らすことができます。

一方でタイミングが悪いと急激に振れが小さくなります。

波動のところで出てきた弦の振動もそうですね。

ある振動数の波を与えると弦は大きく揺れます。

一方でそれ以外の振動数だと、弦はあまり揺れません。

このように、周期的に振動するものについて固有の力や振動を与えることでその振動が大きくなることを「共振」と言います。

交流回路も周期的に振動するものなので同じように共振を考えることができるのです。

共振回路を考えることで何が得られるの？

交流回路で共振を起こすことで、電流や電圧を大きくすることができます。

電流を大きくするか、電圧を大きくするかで特徴が変わってくるのですが、それは具体的にこれから説明していきます。

交流回路の共振は実生活で非常に重要な役割を果たしているので知っておくといいでしょう。

それを踏まえてRLC直列回路とRLC並列回路を見ていきましょう。

RLC直列回路

RLC直列回路に関しては別の記事で詳しく解説しています。

インピーダンスの話と共振回路の話をセットで説明しているのでこちらを確認してくださいね。

交流回路解説！RLC直流回路のインピーダンスとは？

以降でRLC並列回路を詳しく説明していきます。

RLC並列回路

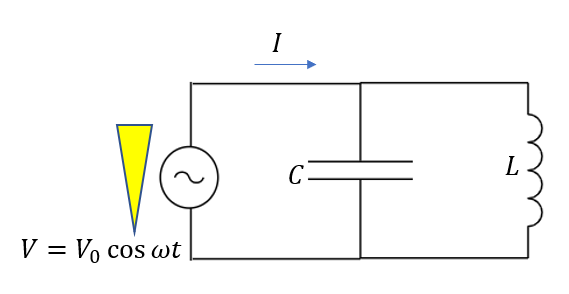
RLC並列回路とはこのような回路を表します。Rとありますが抵抗は今回考えません。

この回路に置いてまずはRLC直列回路と同じようにインピーダンスなるものを考えてみましょう。

つまり、直流に置き換えるとどのような抵抗を置くことになるのかを考えるということです。

電流\(I\)を求めてみよう

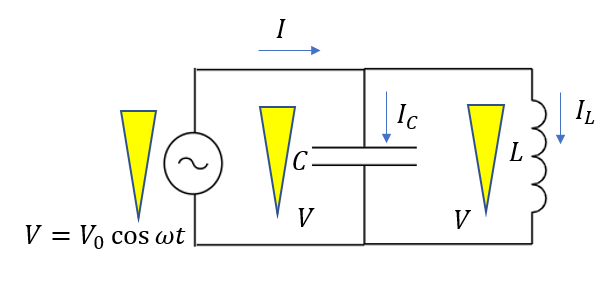
電源の電圧が\(V = V_0\cos{\omega t}\)と与えられている状態で電源から流れる電流\(I\)を求めます。

この\(I\)はコンデンサーとコイルに流れる電流\(I_C, I_L\)を使って

\(I = I_C + I_L\)

と表せるので、この\(I_C,I_L\)を求めればうまくいきそうです。

今回の場合各素子にかかる電圧は電源の電圧\(V\)と等しくなります。

これを元に\(I_C, I_L\)を求めてみましょう。

コンデンサー

まず、交流回路におけるコンデンサーは直流に置き換えると\(R_C = \frac{1}{\omega C}\)という抵抗値をもつ抵抗に置き換えられます。直流に置き換えるとは実効値の関係を表すということなので、以下が成立します。

実効値は「最大値の\(\frac{1}{\sqrt{2}}\)倍」ですから、最大値\(V_0, I_{C0}\)について以下のように表せます。

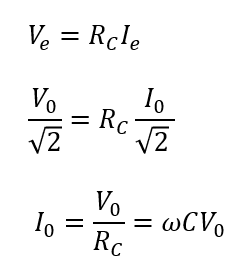
そして、コンデンサーの電流はコンデンサーにかかる電圧より位相が\(\frac{\pi}{2}\)進むことを考慮すると次のように表すことができます。

コイル

まず、交流回路におけるコイルは直流に置き換えると\(R_L = \omega L\)という抵抗値をもつ抵抗に置き換えられます。直流に置き換えるとは実効値の関係を表すということなので、以下が成立します。

実効値は「最大値の\(\frac{1}{\sqrt{2}}\)倍」ですから、最大値\(V_0, I_{L0}\)について以下のように表せます。

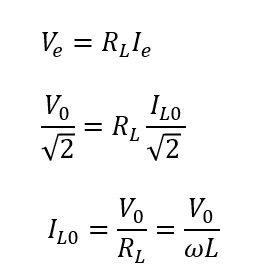
そして、コイルの電流はコンデンサーにかかる電圧より位相が\(\frac{\pi}{2}\)遅れることを考慮すると次のように表すことができます。

ここまでの話はすべてこちらの記事で詳しく書いてありますのでチェックしておいてください。

コンデンサーのリアクタンスって何よ！交流回路のコンデンサーを理解する

位相がずれる、リアクタンスってどゆこと？交流回路のコイルを徹底解説

\(I_C,I_L\)が求まったので\(I\)を式にできますね。

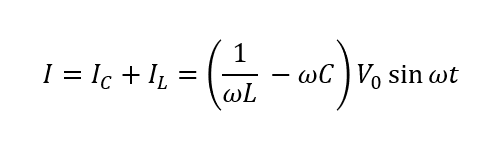
直流に置き換える→実効値を考える

ここから実効値を考えることで直流に置き換えてみます。

実効値を考えるには電流と電圧の最大値が必要です。

上の式から\(\sin{\omega t} = 1\)のときに電流が最大値を取ります。

実効値に直すには両辺\(\frac{1}{\sqrt{2}}\)をかければ良いですね。

そして\(V=RI\)の形にしてみます。

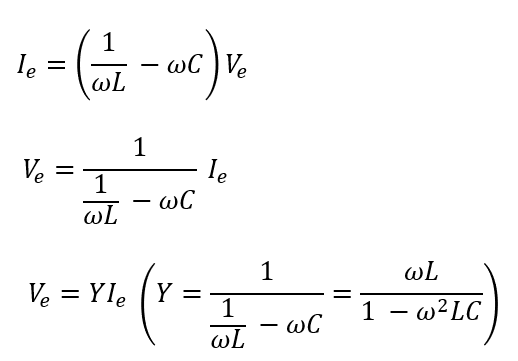
最後の式でオームの法則のような形にすることができました。

つまり、今回の並列回路を直流に置き換えたときに、コイルとコンデンサーは\(Y\)の抵抗値を持つ抵抗に置き換えることができるというわけです。

並列共振回路と固有振動数

では次にこの回路の「共振」を考えます。

最初に伝えた通り、共振を起こすことで電圧や電流を大きくすることができます。

今回は電圧を大きくすることを考えてみます。

電圧をとにかく大きくするにはどうしたらいいでしょう？

ポイントは先ほど求めたリアクタンス（抵抗）です。

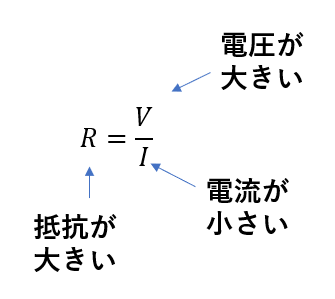
このようにリアクタンス（抵抗）が大きくなれば電圧は大きくなることがわかります。

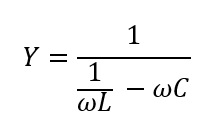
このリアクタンスを極限まで大きくするには・・・

分母が０になれば良いんですね。

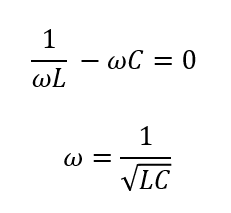
この\(\omega\)は交流の角周波数というものですが、これは交流電源を操作することで変えられます。

つまり、この角周波数にすることで電圧を最大に高められるということです。

これが共振です。

交流並列回路では何が起こる？

この共振が起こったときはどのような状況が起こるのでしょう？

\(Y\)が無限大になるので、\(V\)が限りなく大きくなり、\(I\)は０に近づきます。

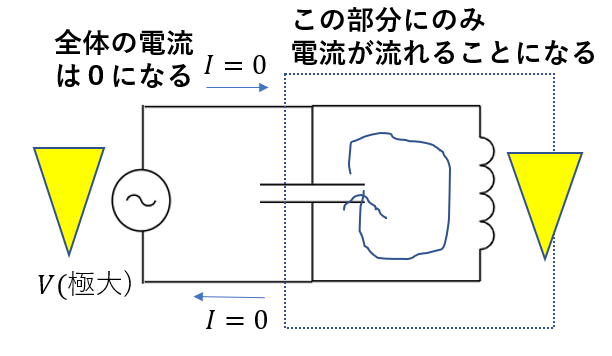
このように、全体の電流\(I\)が消え、コイルとコンデンサーの間だけで電流が流れる状態が起こります。

交流並列回路という問題から考えると→電気振動

まずは、完全に入試問題を解くための考え方です。

実はこの並列共振回路は電気振動と全く同じ形になっています。

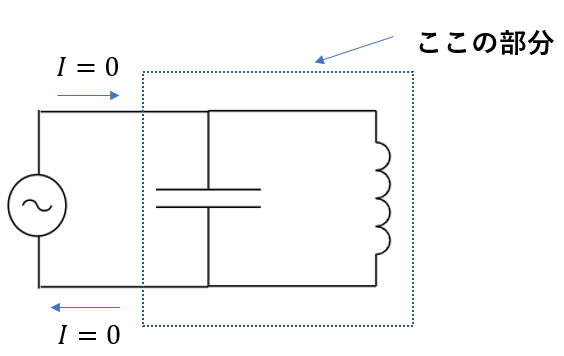
点線で囲った部分だけを見たら電気振動の回路になっていますね。

電気振動の角周波数も実は

\(\omega = \frac{1}{\sqrt{LC}}\)

と表されます。

その理由はこのように、

RLC並列回路が共振したときのコイルとコンデンサーの閉回路を取り除いた部分が電気振動の回路になるからなのです。

ということは逆に言い換えれば、電気振動の問題は

RLC並列回路に置き換えればいい

ということになります。

特に角周波数を求める問題が出たときは、一度並列回路に戻して、共振する条件を求めることで導くことができるようになります。

電気振動に関してはこちらをチェックしてください

電気振動を分かりやすく教えます！コンデンサー2つあるときだって楽勝

実生活という点から考えると→ラジオ

もう一つの視点は実生活です。

実はこの並列回路はラジオなどに使われています。

ラジオの局は電気信号の周波数で分けられています。

そして、最初の段階ではその電気信号が入り混じっています。

ラジオで「ザーー」と雑音に聞こえる理由は複数の電気信号を受信しているからです。

ですが、チャンネルを回すとラジオが聞こえるようになりますね。これは特定の周波数の電気信号だけを取り出すことができたからです。

この「特定の周波数の電気信号を受信する」役割を持つのが並列共振回路なのです。

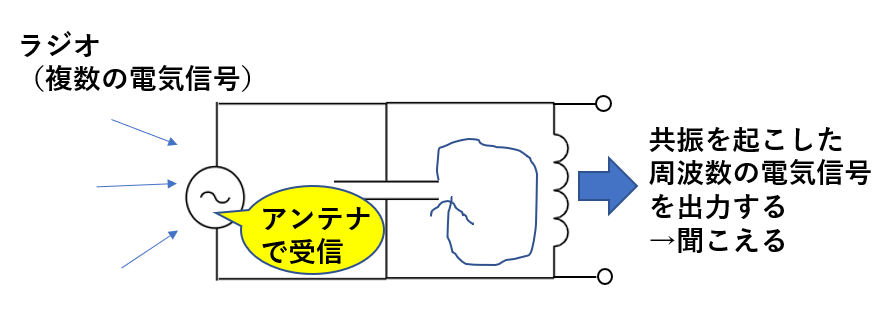
このように、LC並列回路はラジオを選曲するために使われる基本構造なのです。

また共振時の角周波数は\(\omega = \frac{1}{\sqrt{LC}}\)でした。

つまり、\(L,C\)を変化させることで、様々なラジオを聞くことができるのです。

\(L\)はコイルそのものを変えないといけないので変えることは難しいですが、

\(C\)は極板の間隔を広げたり、左右にずらすことで変化させることができます。

このように、ラジオなどの選局に使われていて、実生活で非常に役に立っているのです。

LC並列回路はある周波数以外をカットする働きがあります。

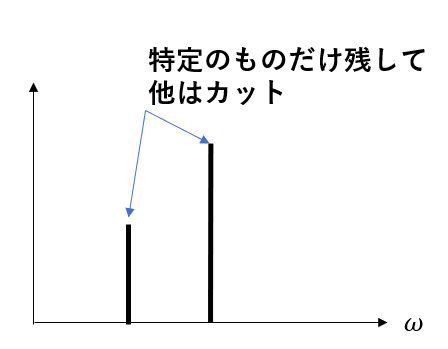
一方でRLC直列回路では「特定の周波数を大きくする」役割があります。

詳しくはこちらをチェックしてくださいね。

交流回路解説！RLC直流回路のインピーダンスとは？

以上2つの見方があります。

2つコンデンサーがある場合は？

最後に応用としてコンデンサーが2つある場合を考えてみます。

これは電気振動の問題でたまにコンデンサーがもれなくもう1つついてくるときがあるので簡単に解説します。

結論から言うとコンデンサーを合成して\(\omega = \frac{1}{\sqrt{LC}}\)の\(C\)にその合成容量を入れればOKです。

ここではそれを示していきます。

（微分の考えが出てきてしまいますので、分からない人はパスしてOKです。）

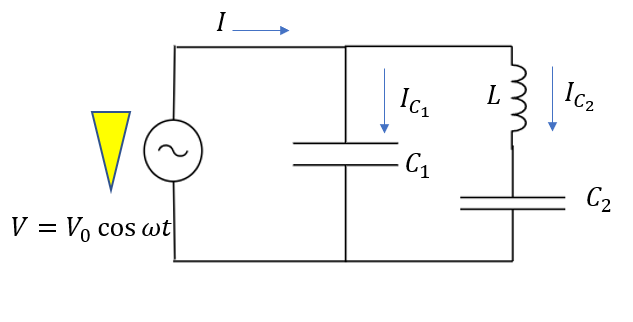
まずはコンデンサー\(C_1\)について

これは難しくありませんね。コンデンサーには交流電源の電圧\(V\)が同じくかかります。

最初に考えたLC並列回路と全く同じ形で、ここに流れる電流\(I_{C_1}\)は表せます。

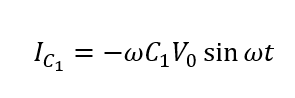
コイルとコンデンサー\(C_2\)について

ここが複雑になってきます。

コイルには誘導起電力が生じます。その大きさは

\(V_L = L\frac{d I_{C_2}}{dt}\)

です。（\(\Delta\)を用いた形でも良いですが、それは微分の記号と同じ意味を表します）

また\(C_2\)の電気量を\(q\)とすると、コンデンサー\(C_2\)の電圧は

\(V_{C_2} = \frac{q}{C_2}\)

となります。

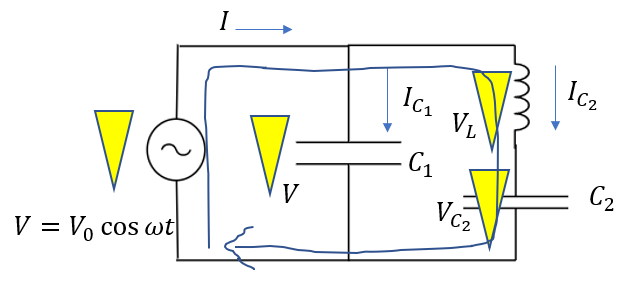
図のようにキルヒホッフの法則を使えば

\(V – V_L – V_{C_2} = 0\)

∴\(V_L + V_{C_2} = V\)

となります。具体的に式を代入すると以下のようになります。

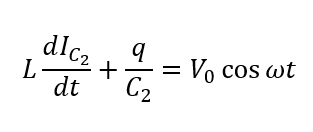
ここで両辺を\(t\)で微分します。この時\(I = \frac{dq}{dt}\)に注意して式を整理します。

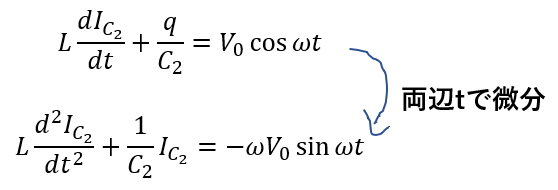
共振条件を使って角周波数を求める

もうすぐです。頑張りましょう。

電流について

\(I = I_{C_1} + I_{C_2}\)

が成立しますね。

ですが\(I_{C_2}\)を求めるのは高校生の知識では無理です。計算も大変です。

そこで共振の条件を使いましょう。

先ほどの例を見ての通り、共振を起こすとき、\(I =0\)となります。

なので

\(I_{C_2} = -I_{C_1} = \omega C_1 V_0\sin{\omega t}\)

となります。

これを先ほど微分を使った式（微分方程式）に代入します。

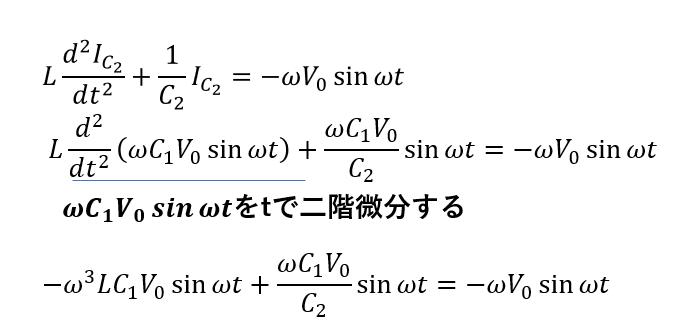
\(I=0\)という条件からここまで導きました。\(I=0\)は共振するための条件です。

つまり、時間\(t\)によらず常に\(I=0\)でなければいけないのでsinの係数を比較すると・・・

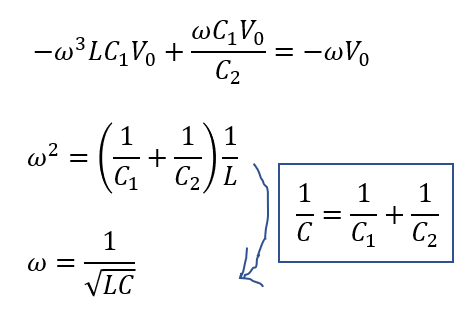
このように角周波数を求めることができます。

2式目から3式目の過程で

\(\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2}\)

となっていますね。

これはコンデンサーの直列接続の合成をしていることになります。

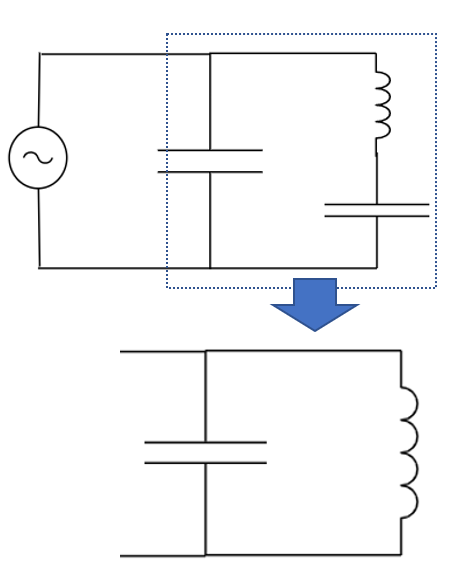
一見並列に見えますが、共振回路は点線の部分を見ることになるのでコンデンサーを直列接続とみなす必要があります。

電気振動でコンデンサー2つある場合の周波数も、この並列回路の共振と同じです。

電気振動についてはこちらを確認してくださいね。

電気振動を分かりやすく教えます！コンデンサー2つあるときだって楽勝

まとめ

いかがでしたか？

RLC並列回路と共振回路について理解ができたでしょうか？

入試という視点で見てしまうと交流は理解が難しいです。

そこを実生活と関連させてみると意外とあっさり理解できてしまうことが多いです。

もちろん、問題を解ければ入試は良いのですが、暗記だけで問題に臨んでも初見問題には対応できないのでこの辺りもしっかり理解しておきましょう。