【高校物理】ガウスの法則の意味って？電場との関係をわかりやすく解説

2019年3月11日

2019年9月25日

WRITER

あっきー

　

この記事を書いている人 - WRITER -

あっきー

オンライン物理塾長あっきー。高3秋から1か月で40点点上げ、センター試験では満点を取り、その経験を活かし塾講師として活躍。塾・学校・参考書の内容やカリキュラムに違和感を感じ数多くの高校生を救うため、大学2年生で「受験物理Set Up」を開設。多くの高校生が活用するサイトに発展し、現在「合格への道」で勉強法に特化した受験サポートを行う。

高校物理の電磁気分野の初めの方にガウスの法則というのを習います。

このガウスの法則はなかなか理解に苦しむ内容なんですね。

ガウスの法則の概念がいまいちわからないということもあり、参考書や教科書ではわかりやすく説明されていないことが多いです。

しかも、問題集ではこれに関する問題はほとんどなく

いきなり入試問題に出てきて手を付けられず終わる。

という受験生泣かせのところなんですね。

そこで、今回はそもそも「ガウスの法則とは？」という意味の部分を、他の参考書にはない方法でわかりやすく説明していきます。

ガウスの法則は「電場を分かりやすく書き換えた」

ガウスの法則というのは結論からいうと

電場を分かりやすく書き換える

というものです。

ここからは電場が関係してくるので電場について全く知らないという方はこちらを確認ください↓↓

電場って結局何？静電気力と電場の意味をわかりやすく説明します

どんな形状の電荷でも成り立つ式を考えた

電場\(E\)はこの記事で説明した通り、二つの点電荷に働く静電気力から考えたものでしたね。

ですから、「点電荷」でしか成り立たない式なわけです。

ですが、電場って別に電気の貯まった棒でも板でも球体でも生じるわけです。それらも式にしてあげたいと思ったのがガウスさんなのです！

ガウスの法則棒でも面でも球でも電場を一般的に表す方法を見つけ出したのです。

そしてガウスはどんな形状の電荷でもこんな関係式が成り立つことを示しました

「電場×表面積＝電荷量」

これがどのように導出されるか、

そしてどういう意味なのかを詳しく見ていきましょう。

ガウスの法則と電場の関係

ここでは点電荷の場合を考えます。

点電荷では\(E = k\frac{Q}{r^2}\)というのが式として分かっています。

つまり初めに紹介した

電場×表面積＝電荷量

と考えてもちゃんと同じ式が成立することを確認していきます。

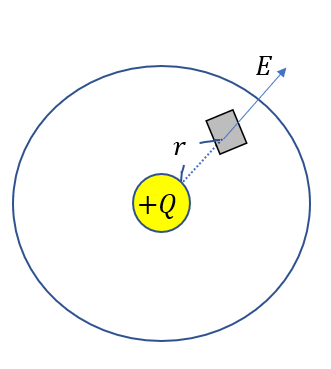
\(+Q\)の点電荷が距離\(r\)の位置に作る電場の大きさを考えたいと思います。

電場は円状に広がっていくので、距離が同じであればどの東西南北のどこの方向にあっても大きさは同じです。

そこで、点電荷を中心に半径\(r\)の球体を考えます。

そして、図のように面1m²を垂直に貫く電場を

\(D = \varepsilon_0 E\)

とします。

この\(\varepsilon_0\)は真空の誘電率という定数です。高校生では「なんかの定数なんだ」という認識で大丈夫です。

電場は四方八方に生じているのですが、この\(D\)は「電場のうちある面１m²を垂直に貫く電場をピックアップしたもの」で、性質は電場と変わらないです。1m²あたりの電場です。

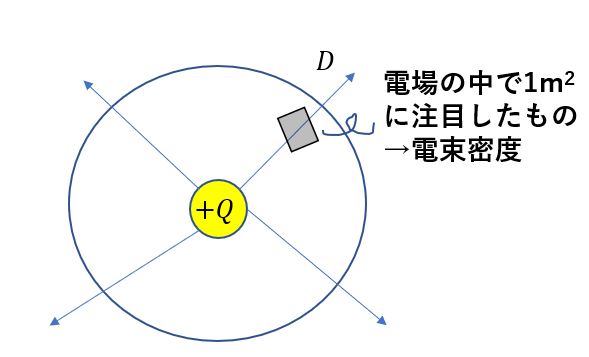
この\(D\)を電束密度と言います。（説明は後程）

この\(D\)は1m²あたりの電場なので、これに表面積を掛けてやれば電場全体が出ます。

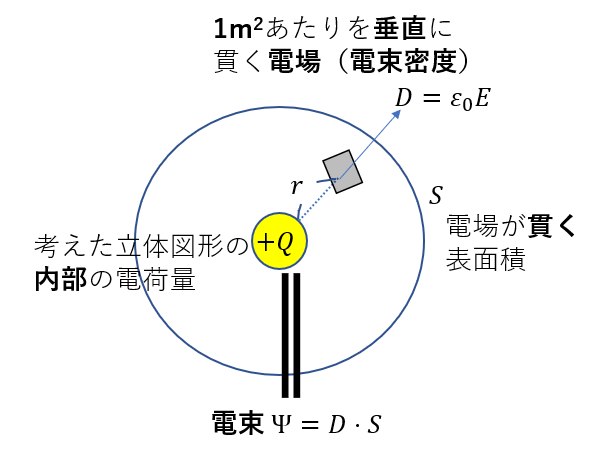
そしてガウスはこの電場全体が囲んだ図形内の電荷量に等しいということを見つけたのです。

つまり、

\(D S = Q\)

ということです。

\(D = \varepsilon_0 E\)であり、

\(S\)はここでは球の表面積なので、

\(S = 4\pi r^2\)ですね。

なので、具体的に

\(\varepsilon_0 E \cdot 4\pi r^2 = Q\)

となります。すると・・・

\(E = \frac{1}{4\pi \varepsilon_0} \frac{Q}{r^2}\)

この\(\frac{1}{4\pi \varepsilon_0}\)

は定数なので、改めて\(k\)と置けば・・・

\(E = k\frac{Q}{r^2}\)

このように式も一致したので点電荷ではガウスの法則

\(DS = Q\)

が成立することがわかりましたね

ついでに

静電気力や電場で出てきた\(k\)というのはこの途中で見た通り

\( k = \frac{1}{4\pi \varepsilon_0}\)

とかけることもわかりましたね。

棒、面、球状でも成立するの？

このガウスの法則は電荷の形がどんなものであっても成立することが分かっています。

ただ高校生の範囲では説明するには無理がありますので、ここは省略しますが数式的に証明されていることなので間違いはありませんし、例外もありません。

なので安心して使ってくださいね。

もっと言えば、電荷を囲う図形の形状も全く関係ありません。自分の好きに取っても構いません。

先ほどの点電荷の場合も球じゃなくて、立方体でも、もっといびつでもなんでも構いません。

ただ、その電荷の形状に合ったものを選ばないと、計算が複雑になってできない場合があるので好きに選んでも良いと言っても計算できるように選ぶ必要があります。

ガウスの法則は分かりやすくて超万能

説明が長くなってしまったので要点をまとめましょう。

ポイントこれです。

\(DS\)（ゲーム機ではない）

というのは実は電場全体ということで「電束」という名前がついています。聞いたことないかもしれませんが、「磁束」というのは習った人もいるかもしれません。それの電気バージョンと思ってもらえればOKです。

このガウスの法則にはいくつか注意点があります。

• 立体図形はなんでもOK

先ほど説明した通り、電荷を囲う形状はなんでも構いません

ただ、図形によって計算ができなくなるので注意です。

• Dは定義に注意

\(D\)の定義は「1m²あたりの電場」と言いましたが厳密にはこうです。

1m²あたり垂直に貫く電場

「垂直」です！

つまり、

「全電場が垂直に貫くように立体図形を決めろ！！」

これが問題で重要になります。問題演習の際に確認しましょう。

• \(Q\)は図形内部の電荷量

問題では、平面の電荷について考えるケースがあります。

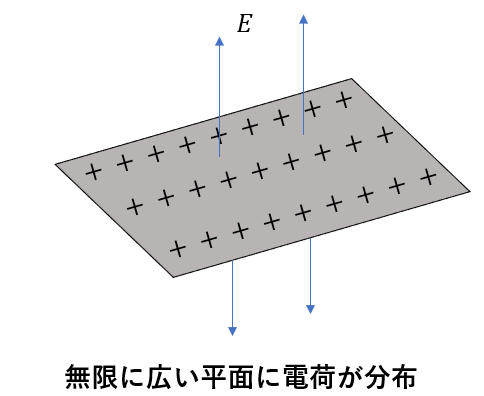
この電荷が作る電場の大きさを考えるときに、もちろん図形を考えますよね。

でも無限に広いので、すべてを囲うのは無理です。

なので、一部分を囲います。

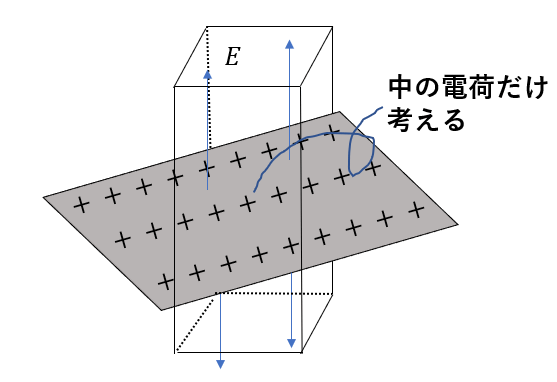
この時に、電荷が図形の内と外で分かれますよね。

ここで使うのは内部の電荷です。

外側は完全に無視してください。

実際に問題演習を別でやってみましょうね。

問題で使ってみてこそ自分のものになる

いかがでしたか？

そこらへんの教科書や参考書では書いていない内容だったと思います。こちらの方が分かりやすいと思っていただければ嬉しいです。

とはいえ、実際に使ってみないと自分のものになりません。受験は理解しても実際に使えなければ点数はもらえないのです。

なので、実践問題でガウスの法則の使ってくださいね。