ガウスの法則の問題解説!東京理科大の過去問で理解しよう
ガウスの法則の使い方が分かる
ガウスの法則の理解が深まる
入試レベルの問題も楽々解ける
こんにちは。
Akinoriさん!ガウスの法則の記事でこの法則の意味がわかりました!
 AI
AI
それは良かったです!
 AKINORI
AKINORI
でも、実際に使ってみないと本番でできるかわからないので不安です・・・
 AI
AI
だよね。やっぱり演習で適用できるようにしないとね。今回はいきなり入試問題にチャレンジしてみよう!
 AKINORI
AKINORI
ガウスの法則についてはこちらの記事で教えています。
ただ、ここではガウスの法則の意味と使い方について説明をしただけです。
理解しても実際に問題で使いこなせなければ意味がありません。
そこで、今回は東京理科大の入試問題を持ってきました。良問です。これが解ければガウスの法則はまず問題ないと思います。
必ず上の記事を見ておいてくださいね。
東京理科大のガウスの法則の問題
図のように、半径\(a\)の導体球を置き、外半径\(c\)の球形導体殻でおおう。内側の導体球の中心と外側の導体殻の中心は一致しており、内側の導体球と外側の導体殻にはそれぞれ\(Q,q > 0\)の電気量が蓄えられている。真空の誘電率を\(\varepsilon_0\)として以下の問いに答えよ
なお、電荷は導体球や導体殻の表面に一様に分布し、導体内部は電場が生じないことが知られている。

(1)導体殻内側および外側のの電気量の大きさをそれぞれ求めよ
(2)導体は球形をしているので、原点Oに関して対称的である。このことから原点Oからの距離\(r\)の位置における電場の強さは\(a < r < b\)のときどう表されるか?また\(c < r\)のときはどのように表されるか?
(物理重要問題集2019 問100 東京理科大(改))
もちろん使うべきはガウスの法則です。絶対にやってはいけないのは
\(E = k \frac{Q}{r^2}\)
を使うことです。これは「点電荷」の場合にのみ成り立つ式です。
今回はどう見ても「点」じゃないですよね。こういう場合はガウスの法則を使う以外ありません。それを頭に入れておいてまずは自力で解いてみましょう。
電気量についてもガウスの法則で解こう
問題文にあるように、導体表面に電荷が現れ、導体内部の電場は必ず0になります。
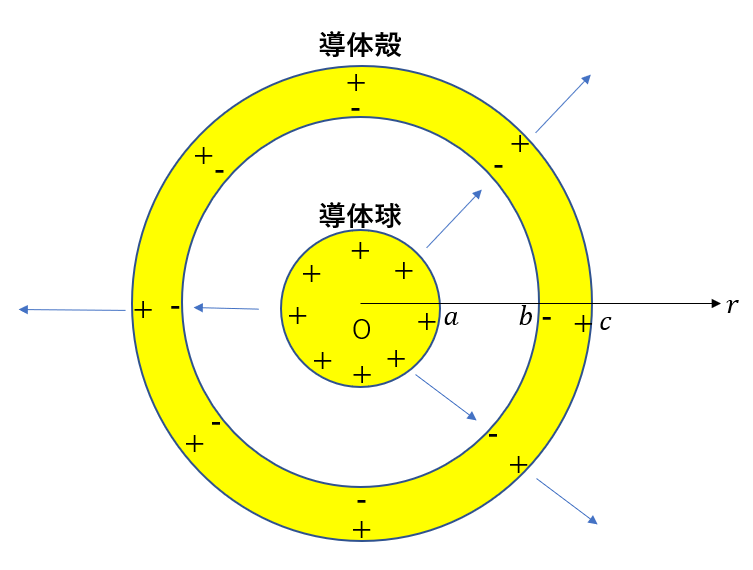
図のようになりますね。
内側の導体球は正に帯電していますから、導体殻の内側は負の電荷が、外側には正の電荷が現れることは理解できますね。
そして、二つの導体の間と外側に電場が外向きに生じているのも分かりますね。
これを踏まえて(1)を考えましょう。
もちろん使うのはガウスの法則です。ガウスの法則ではまず、好きな立体図形で囲っていきます。
今回はこのように囲いましょう。
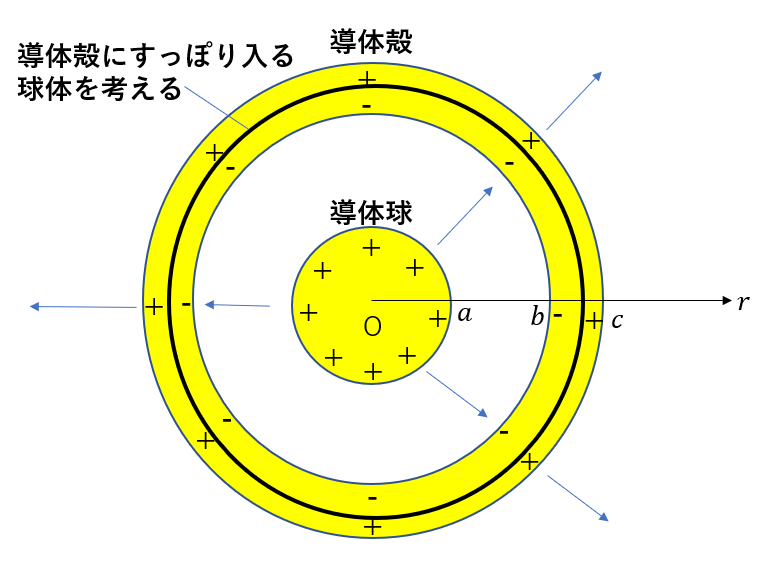
このように導体殻にすっぽり入る球体\(a < r < b\)を考えてみます。
これでガウスの法則を適用してみます。ガウスの法則の法則はこうでしたね。

左辺は電場がそもそもないので0になります。
右辺は今設定した球体内の電荷量の総和になります。導体球の電荷量は\(Q\)と与えられてて、求めたいのが導体殻の電荷量なのでこれを\(Q_{in}\)とすると
\(Q + Q_{in} = 0\)
つまり
\(Q_{in} = – Q\)
となりますね。確かに負の電荷が現れていますね。
外側の電荷量\(Q_out\)も考えます。
導体殻のもともとの電荷量は\(q\)と問題文にあります。そして、電荷は外部に出入りできないので、電荷量は常に一定のはずですよね(電荷保存則)
つまり
\(Q_{in} + Q_{out} = q\)となり
\(Q_{out} = Q + q\)
と答えが出ました。
困ったらガウスの法則で求める
では(2)に進みます。
電場を求める問題なので明らかにガウスの法則を使うことが分かりますね。
最初に伝えましたが、これは球体であり、点ではありません。
なので、\(E = k\frac{Q}{r^2}\)は使えません。
ガウスの法則を適用するわけですが、先ほどと同様にまずは自分で立体図形を決めます。
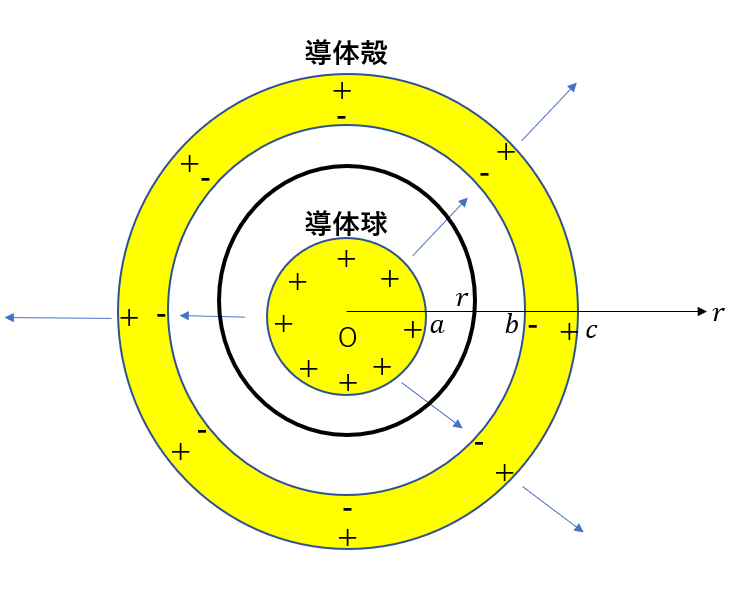
まずは\(a < r < b\)の電場を求めたいので、図のように二つの導体の間にある半径\(r\)の球体を考えます。
先ほどと同じようにガウスの法則\(DS = Q\)を適用します。
\(D\)は\(D = \varepsilon_0 E\)です。
また\(S\)は球の表面積なので
\(S = 4\pi r^2\)となります。
そして右辺の\(Q\)は図形内部の総電荷量で、今回は導体球の電荷量\(Q\)に相当します。
ということでそれぞれ式に代入すると
\(\varepsilon_0 E \times 4\pi r^2 = Q\)
∴\(E = \frac{1}{4\pi r^2} \frac{Q}{r^2}\)
はい、求められましたね。
あ。解けてる・・・あれ?これって点電荷の場合と同じじゃん!
 AI
AI
そう。実は球体なら点電荷の場合と同じように表せるんだ
 AKINORI
AKINORI
何となくそんな気がしていたかもしれませんが、点電荷と同じ形なんですね。
次は外側の部分\(c < r\)を考えます。やることは全く同じです。
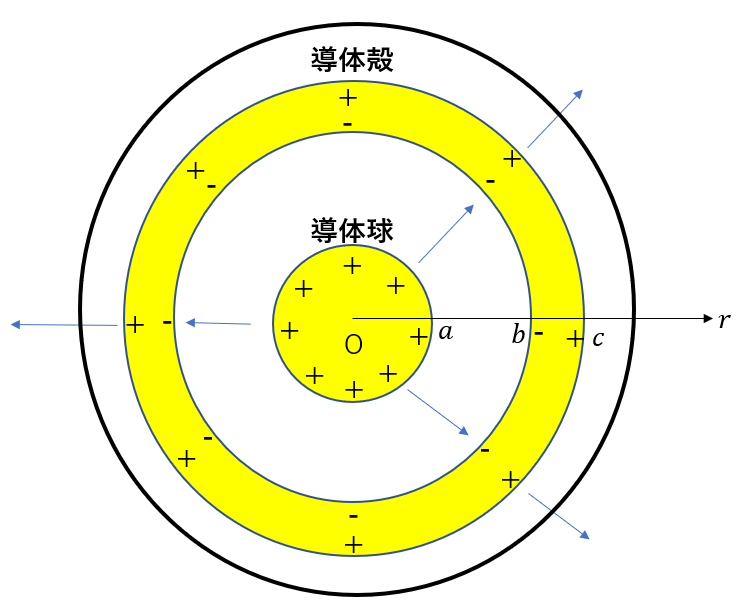
同じように半径\(r\)を考えます。
\(D, S\)は先ほどと同じです。
変わるのは右辺の\(Q\)だけですね。立体図形の内部の電荷の総量なので
\(Q + q\)
となります。
なので答えは
\(\varepsilon_0 E\times 4\pi r^2 = Q + q\)
\(E = \frac{1}{4\pi \varepsilon_0} \frac{Q + q}{r^2}\)
となります。
なんか簡単すぎてびっくりしました!ガウスの法則の問題なんてなんでも解ける気がします。
 AI
AI
ちなみに、この手の問題は最後に「これをコンデンサーと見立てたときの電気容量を求めよ」と来ることが多いです。ここではテーマに逸れるので説明しませんが、考えてみてもいいですね。
ガウスの法則をうまく活用しよう
いかがでしたか?
これは物理重要問題集から持ってきましたが、その解説にはこう書いてあります。
「点電荷であると見なし・・・」
何の根拠もなくいきなりこのように仮定しているので腑に落ちない人もいるのでは?と思います。
ガウスの法則を使って求めた結果、たまたま点電荷の場合と同じ式になっただけです。
球体じゃなかったらこんな仮定は間違っているわけです。
ですが、ここで問題を解いたあなたなら仮定とか一切せずとも、どんな形状の電荷でも解くことができますね。
これでガウスの法則は攻略です。おめでとうございます!