磁束密度って何ぞや？磁場との違いを分かりやすく説明してみた！
Akinoriさん。今日ね、学校の授業で「磁束密度」っていうの習ったんですけど、これ全然意味わからないんです。磁場と何が違うわけ？っていうか「磁束」って何ですか？
AI
・・・今日は勢いがすごいね。僕も最初は磁束密度ってなんだよって思ってました。なのでわかりますよ、その気持ち。今日は磁束密度について考えてみよう！
AKINORI
学校の授業や、教科書でいきなり出てくる「磁束密度」これについてイメージがわかなくて理解できない！！
そんな風に悩んでいませんか。
磁場と磁束密度の違いってなんやねん！！
少なくとも僕はこうやって思ってましたね。
ということで今回は、磁束密度って何？
という疑問を解決したいと思います。
磁気と電気は似すぎてる！？
まず先に言っておくと、磁気と電気はめっちゃ似ています！！なので、電気で言えたことは基本的に磁気にも言えます。
AKINORI
ということなので、まずは電気について必ず確認しておいてください！！
電気に関しては電荷があって、正と負の二種類ありましたね。
磁気に関しても磁荷があって、NとSの二種類があります。
そして、二つの電荷が及ぼしあう静電気力はこうやって表せましたね。
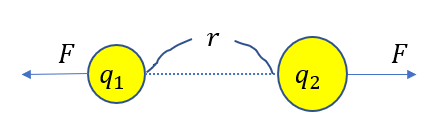
\(F = k\frac{q_1q_2}{r^2}\)
\((k = \frac{1}{4\pi \varepsilon_0})\)
この関係が、磁気にも言えるというのです！！
磁荷量\(q_1, q_2\)をもった ”点磁荷” が及ぼしあう静磁気力は・・・
\(F = k_m\frac{q_1q_2}{r^2}\)
\((k = \frac{1}{4\pi \mu_0})\)
- 同極なら反発
- 異極なら引き合う
この\(\mu_0\)は「真空の透磁率」というもので、電気でいう「真空の誘電率」\(\varepsilon_0\)です。
また、磁場も全く同じように、静磁気力を遠隔力と考えるのは嫌なので、
磁荷を置くと磁場というのが現れ、その場によってほかの磁荷が力を受ける。
こう考えたわけですね。
そして、電荷量\(q_A\)の点電荷が作る電場の大きさ\(E\)はこう表せました
\(E = k\frac{q_A}{r^2}\)
これは、＋１[C]の電荷が受ける静電気力と同じということでしたよね。
全く同じように、
磁荷量\(q_A\)の ”点磁荷” が作る磁場の大きさ\(H\)は・・・
\(H = k\frac{q_A}{r^2}\)
＊＋１[Wb]の点磁荷が受ける静磁気力
なるほど！電気と磁気は何らかの関係があるみたいですね！
AI
そうだね。二つは非常よく似ていて、関連が深いことが分かるね。
AKINORI
さっきから思ったんですがなんで “点磁荷” って書いてあるんですか？普通に「” ”」をつけないでいいのに・・・
AI
これが、電気と磁気の一番の違いで、磁荷には”点磁荷”ていうのが本当は存在しないんだ。
AKINORI
電荷は、正電荷、負電荷を単体で取り出すことができます。
電子とかはまさに「負電荷」ですよね。
ですが、磁荷はそうはいかないんです。
磁荷はN極とS極が絶対にペアで存在するんです。
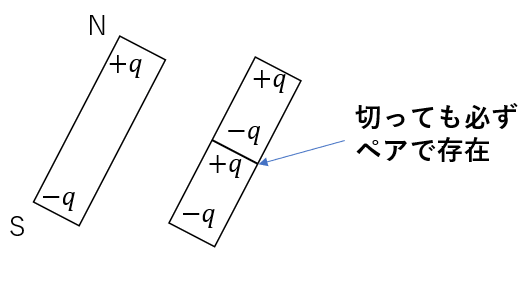
そうすると、N,S極それぞれが作る磁場を合成しないと本来の磁場って出ませんよね。
それだと電場のようなきれいな式が得られないです。
ですが、”点磁荷”を考えることで、点電荷の電場と同じような磁場の式を導けるのです。
ここまでの話は最初に紹介した記事を見ている前提で話しているので、意味わからない人はこの記事を読んでください。
この後の話もこれを読んでる前提で話します。
磁束密度もやっぱり同じ？
じゃあ、いよいよ本題ね。電気のところで「磁束密度」に似たことやらなかった？
AKINORI
そう言えば、Akinoriさんの記事で「電束密度」ってやった気がする。確かガウスの法則で・・・ってまさか！？
AI
そう！同じことがやっぱり磁気のところでも言えるんですね。
AKINORI
高校の教科書ではなぜか「磁束密度」は出てきて、「電束密度」が出てきません。
だから、いきなり磁束密度が出てきて困るんですよね。
ですが、電気分野にも当然「電束密度」という概念はあります。
また、電場については「ガウスの法則」があるのに、磁場についてはガウスの法則が書かれていません。
ですが、磁気分野にも当然「ガウスの法則」があります。（ただ、今後出てこないです（笑））
電気分野で出てきたガウスの法則はこういうやつでした。
ガウスの法則
\(DS = Q\)
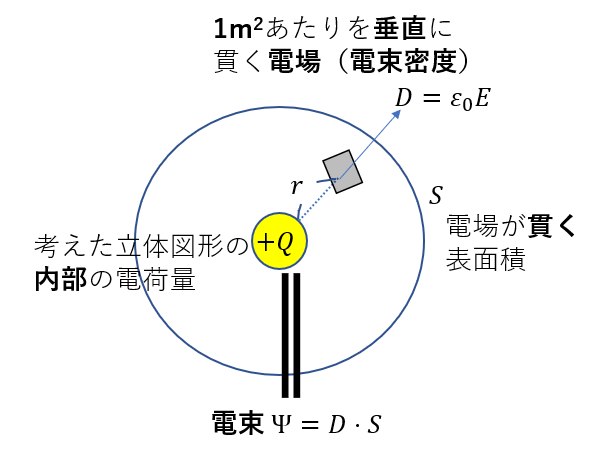
\(D,S,Q\)にはいろいろ注意することがあったんですが、それはさっき紹介した記事に書いてあるので省略します。
となれば、当然同じことが磁場にも言えるわけですよ。
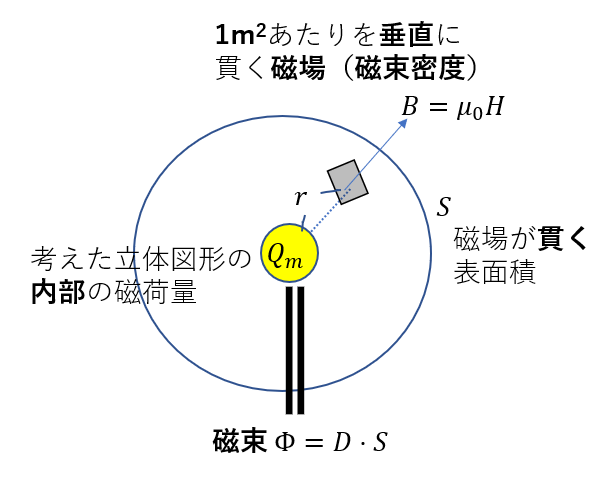
電場でのガウスの法則と比べれば
- 磁束密度：\(B = \mu_0 H\)
- 磁束：\(\Phi = BS\)
と表せるのが分かりますね。
電場の場合と同じように、これをみれば
磁束密度\(D\)は磁場のうち、ある面１m2を垂直に貫く磁場をピックアップしたものです。
ですから、性質は磁場と変わらないです。
磁束密度と磁場は見方の違いだけです。
そして、ガウスの法則は
\(BS = Q_m\)
と表せるわけです。
が、このガウスの法則は今後使いません。
なんでですか？
AI
それは右辺の\(Q_m\)を考えればわかるよ。
AKINORI
右辺の\(Q_m\)は「立体図形の内部の磁荷量」です。
さて、思い出してください。磁荷ってどのように存在するんでしたっけ？
必ずペアで存在する！！
ということは、プラスマイナスで相殺されて\(Q_m = 0\)となります。
つまり、右辺は必ず０なのです。
つまり、立体図形を考えると、何も得られない式になってしまうので、今後使いません。
（だから、教科書では載っていないのかな？）
でも、そしたら\(B = 0\)ということになっちゃいません？でも、磁場が生じているのは確かですよね？
AI
これはあくまで「立体図形を考えると磁束が０」という意味で、磁場が０という意味ではないんです。
AKINORI
今後も磁束を扱う場面があります。その時は、立体図形ではなく「面」を考えます。
また、今後は「磁荷」っていうことは考えないのでこの話はそんなに深く考えないでOKです。
ただただ、磁束密度を理解するためにこういう話を持ってきただけですので。
まとめ
電気と磁気は非常に深い関係性があります。電気で言えた式は、磁気に関してもだいたい言えますよね。
そう考えれば磁束密度も磁束も理解がスムーズにできるはずです。
そして、磁場と磁束密度の違いでしたが、そんなに違いがないです。見方の違いだけですので、本質は同じです。磁束密度＝磁場という認識で問題ありませんね。
それでは！！
