くし形コンデンサーの問題を解説します!

今回は、コンデンサーの演習問題をしていこう!!
くし形コンデンサー
今回扱うのは、「くし形コンデンサー」っていうものです。
「くし形」だから何か特別なことをするわけじゃないんですけど、コンデンサーをしっかり理解できていないと解けません。
頑張りましょう!!
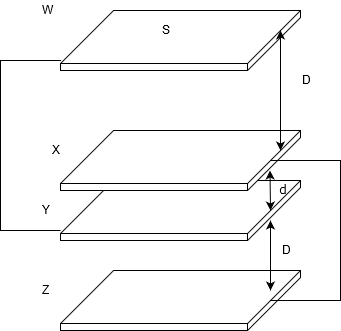
| 問題 面積Sの4つの金属板を図のように並べる。金属板WとY、XとZは導線でつながっており、WとX、YとZの間隔はともにDであり、XとYの間隔はdである。また真空の誘電率を\(\varepsilon_0\)とする。WのX側の表面には電荷Q(>0)が現れるとして、次の問いに答えよ。
(1) WX間の電場の大きさを求めよ。 (2) XY間の電場の大きさを求めよ。 (3) XのY側に現れる電荷を求めよ。 (4) YのZ側の電荷を求めよ。 (5) WとYを一方の極板、XとZをもう一方の極板としたときのコンデンサーの電気容量を求めよ (セミナー物理2016 問454) |
今回のポイントは次の3つ
- 「一周した電位=0」
- 向かい合う電荷の大きさは同じ
- 合成容量の求め方
まずは自力で解いてみよう!!
何にも手が付かない人は次の記事をチェックしよう
解答
(1)
これは、コンデンサーの超基本的なことです。
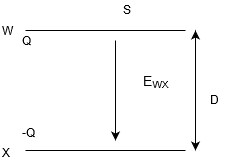
ガウスの法則が分かっていれば解けます。一応ガウスの法則をおさらいしておこう。
詳しく理解するにはこちらをチェック。
| ついでに確認! |
ガウスの法則とは・・・
「電場E = 1[m2]あたりの電気力線の本数」
です。
ちなみに、電荷Q[C]から出る(入る)電気力線の総本数は\(4\pi kQ\)本です。
ですから、今回の問いの電場\(E_{WX}\)はこう書けるわけです。
\(E_{WX} = \frac{4\pi kQ}{S}\)
今回は、真空の誘電率\(\varepsilon_0\)を使わないといけないんですが、
\(\varepsilon_0 = \frac{1}{4\pi k}\)と書けます。
ですので、
\(E_{WX} = \frac{Q}{\varepsilon_0 S}\)
が答えですね。
(2)
ここで、使うのはポイントの1,2です。
- 「一周した電位=0」
- 向かい合う電荷の大きさは同じ
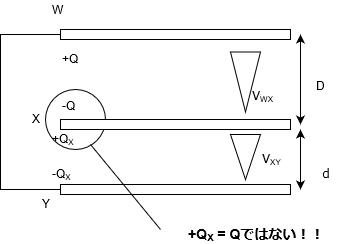
ここで、注意してほしいことがあります。
確かに、向かい合う極板の電荷の大きさは同じです。
でも、実はこれって厳密ではないんですよね。なので、ここで修正しておきます。
「向かい合う極板の表面の電荷は同じ」
この表面ってのが重要です。
よく見れば、Xの上下で電荷の大きさを変えていますよね。一見
\(Q_X = Q\)
って感じになりそうですよね。でも、これは違います。
XはZと導線でつながっていますから、電荷はXとZを自由に行き来できるんですよ。
だから、Xで必ずしも上下で電荷の総和が0になる必要がないんだ。
もし、XがZとつながっていないのであれば\(Q_X = Q\)です。(ただ、その場合極板間隔は同じになるよ)。
ま、それが分かったところで、後は「一周した電位=0」とすればいい。
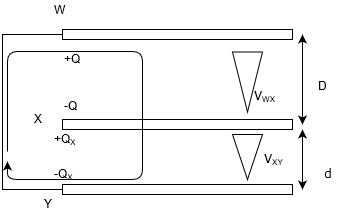
\(-V_{WX} – V_{YZ} = 0\)
\(V_{YZ} = -V_{WX}\)
さて、コンデンサーには一様な電場が生じているよね。
なので、\(V_{WX} = E_{WX}・D\)、\(V_{XY} = E_{XY}・d\)となるわけだ。
| ついでに確認! |
∴\(E_{XY}・d = -E_{WX}・D = -\frac{QD}{\varepsilon_0 S}\)
\(E_{XY} = -\frac{QD}{\varepsilon_0 Sd}\)
(このマイナスってのが次の問いで重要になります!!)
今回は大きさを聞かれているので
\(|E_{XY}| = \frac{QD}{\varepsilon_0 Sd}\)
が答えです。
(3)
さて、これは(2)がしっかり解けていれば問題ないです。さっき\(E_{XY}\)、つまりXY間の電場がマイナスで出ていたよね。
これは、自分で考えていた電場の向きとは逆だったって意味なんだ。
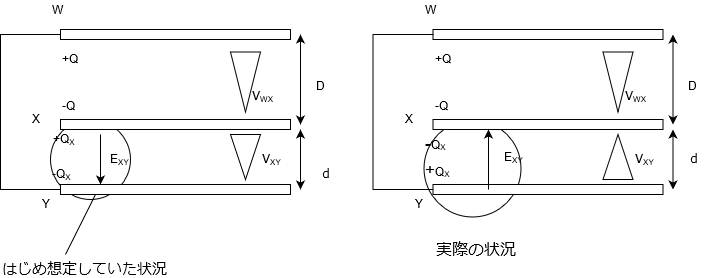
ってことは、BのC側の電荷は実は\(-Q_B\)と、マイナスの電荷だったってことだ。
だから、今回の問いでは、マイナスで答えないといけないってこと。
これに気を付けていれば大丈夫。
というより、しっかりした解き方ができていれば、こんな感じで勝手に答えが出るから安心してね。
(1)と同様、ガウスの法則を使えば(わかりにくいので、とりあえず大きさだけ)
\(| E_{XY} |= \frac{Q_X}{\varepsilon_0 S}\)
∴\(Q_X = \frac{QD}{d}\)
実際は\(-Q_X\)が答えとなるので
\(-Q_X = -\frac{QD}{d}\)
これが答えですね。
(4)
これは(1)~(3)と同じことをすればいいだけだ。
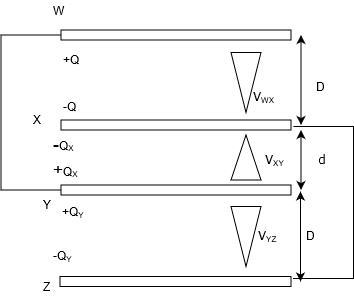
求めたいのは\(Q_Y\)ね。
でも、同じ解説をするのはつまらないので、ちょっと工夫します。
この図を180度回転させてみてください。
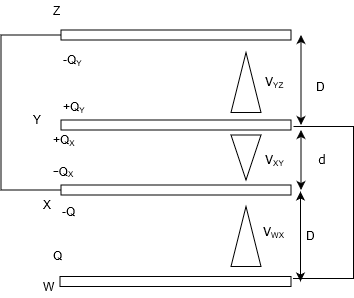
・・・
最初の状態と似すぎじゃん!!
どれくらい似てるかっていうと、電荷の符号がすべて逆になっているだけで、あとはおなじですよね。
だから、\(Q_Y = Q\)になるよね。
これが答えです。これが納得いかないならば、(1)~(3)の作業をもう一度行ってみてください。
(5)
これはちょっと難しい。
まず、問題の意味なんだけど、
たとえばWとX, YとZを互いに向かい合わせにコンデンサーを作って合成しろ
ってことなんだ。
コンデンサーの合成を行うには、とりあえず簡潔な回路にしてしまうのがベスト。
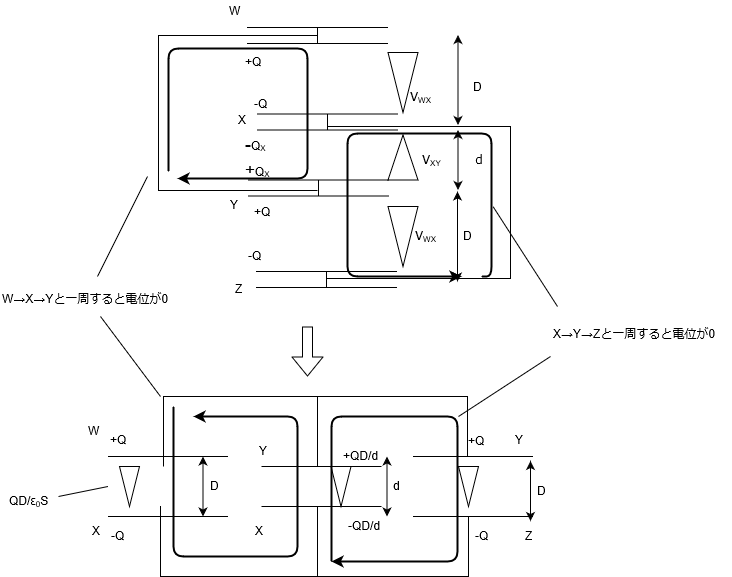
このとき、性質を変えないように変形しないといけない。
だから、「一周した電位=0」に注目して分けるといいと思う。
ではでは、合成容量を求めよう。
合成容量はとにかく全体を見て考えてやれってことだ。
全体で貯まる電気量は
\(Q_s = Q + Q + \frac{QD}{d} = Q\left(2 + \frac{D}{d} \right)\)
また、全体の電圧は
\(V_s = \frac{QD}{\varepsilon_0 S}\)
ってことで、\(Q = CV\)より
\(C = \frac{Q_s}{V_s} = \varepsilon_0 S \left(\frac{2}{D} + \frac{1}{d} \right)\)
これが答えです。
以上で、終わりです。
ちょっと難しかったかもしれないけど、やっていることは単純です。
やっぱり「一周した電位=0」は重要だ!!