テブナンの定理とは?回路問題で簡単に電流を求める方法

どうも!オンライン物理塾長あっきーです
 あっきー
あっきー
回路問題で電流を求めるときにキルヒホッフの法則使うと計算が面倒になります!何とかなりませんか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
複雑な回路では、電流を求めるのにキルヒホッフの法則を使うと式が多くなってしまいます。
計算ミスもしやすくなって怖いですよね。
実は複雑な回路において電流を求める際に使える裏ワザがあるのを知っていましたか?
この記事では、複雑な回路問題で電流を素早く簡単に求める方法を教えます。
また例としてホイートストンブリッジの検流計に流れる電流を求めていきます。
アッと驚く裏ワザですので最後まで読んでくださいね。
テブナンの定理が理解できる
複雑な回路で素早く電流が求められる
ホイートストンブリッジ回路の検流計の電流が求められる
目次
キルヒホッフの法則を使えばすべて求められる

回路問題で電流や電位差を求めるにはキルヒホッフの法則を使うのが普通です。
キルヒホッフの法則が一番本質的でどんな問題でもこれを使えば間違いありません。
しかし、1つ大きなデメリットとして回路が複雑になるほど式が煩雑になります。
そのデメリットを解消する方法というのがテブナンの定理です。
複雑な問題で電流を求める方法:テブナンの定理
![]()
テブナンの定理は「複雑な回路を単純な回路に置き換える方法」のことです。
学校や参考書では取り上げられない話なので、知らないかと思います。
特定の電流だけを知りたい場合に使える
テブナンの定理は特定の電流だけを知りたいときに使えます。
一方でキルヒホッフの法則はすべての電流を知りたいときに使えます。

例えば、ホイートストンブリッジの検流計に流れる電流を知りたいとき、キルヒホッフの法則を使おうとすると式がめちゃめちゃ多くなります。
しかし、検流計に流れる電流だけ知りたいのであればテブナンの定理が非常に有効なのです。
テブナンの定理の使い方を見ていきましょう。
テブナンの定理の使い方
次のような回路で抵抗\(R_1\)に流れる電流\(I_1\)を求めてみましょう。
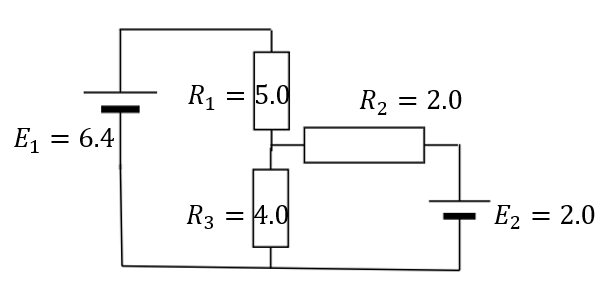
テブナンの定理は次の手順で使います。
- 求めたい電流の領域を切り取る
- 切り取った部分の電位差を求める
- 元の電源を外して合成抵抗を求める
- 1,2,3の抵抗と電池を直列につなぐ
求めたい電流の領域を切り取る
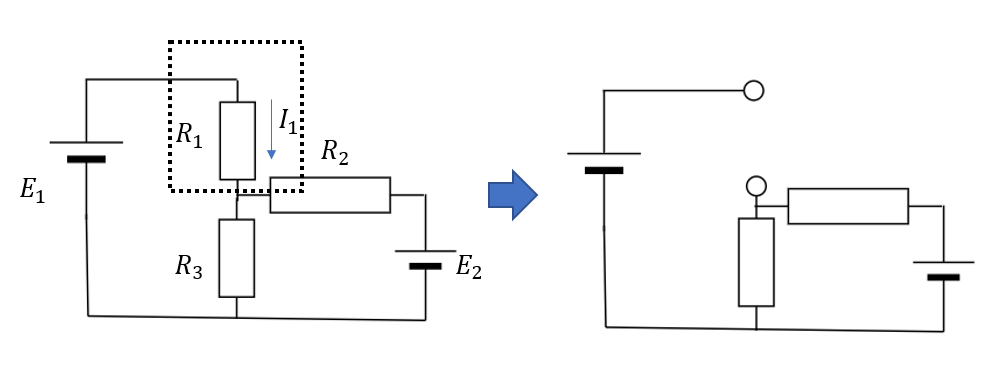
抵抗\(R_1\)の電流を求めたいのでこの領域を切り取ります。切り取ったら断線扱いになります。
切り取った部分の電位差を求める
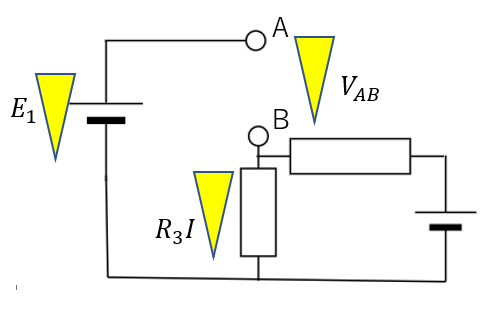
切り取った部分AB間の電圧を求めます(開放電圧)。
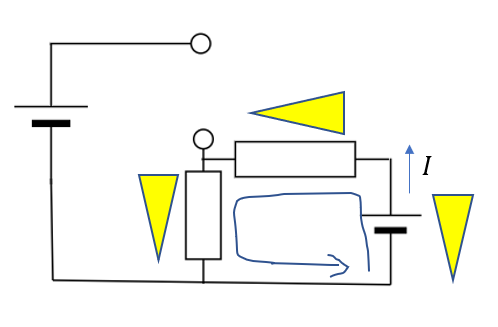
まず図のようにキルヒホッフの法則を使って電流を求めます。
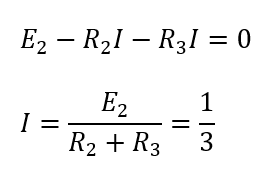
これで抵抗\(R_3\)の電圧降下も求まるので電位差\(V_{AB}\)が求まります。
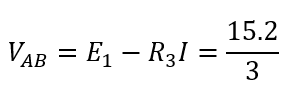
元の電源を外して合成抵抗を求める
次に元の回路の電源をすべて外し、\(V_{AB}\)を電源と見立てたときの合成抵抗を求めます。
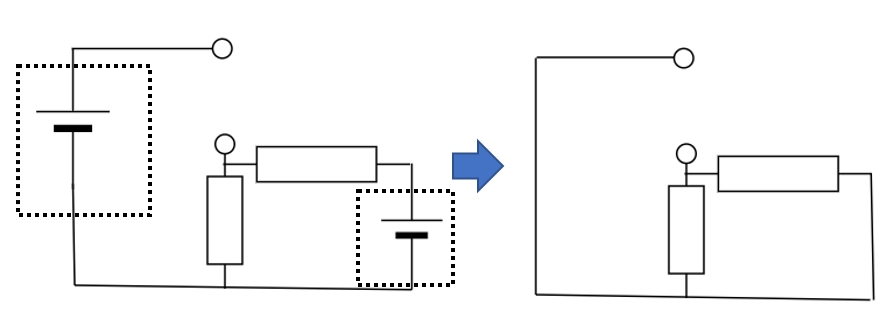
電源を外しますが断線にするのではなく、導線として扱います。
この回路を合成抵抗ですが、これは並列となっています。
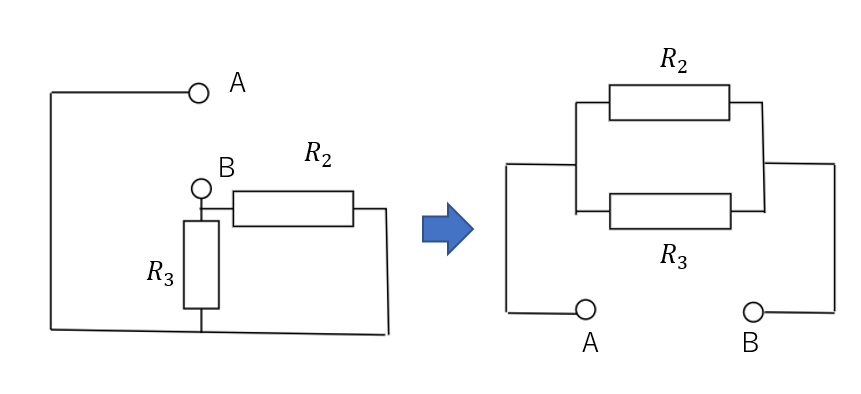
これが分かれば合成抵抗は簡単に求められますね。
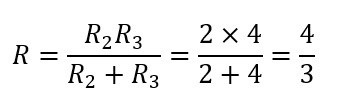
1,2,3の抵抗と電池を直列につなぐ
1で外した抵抗、3で求めた合成抵抗、そして2で求めたABの電圧を持つ電源を直列につなぎます。
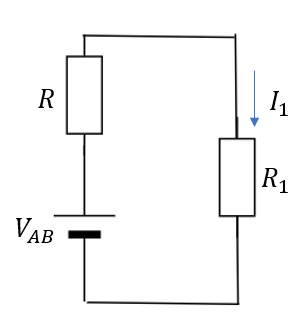
この回路で求めた電流が最初に求めたかった電流となります。
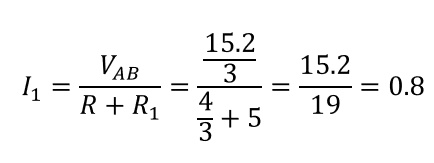
これがテブナンの定理です。
こうすることで特定の電流を素早く簡単に求めることができます。
ホイートストンブリッジの検流計の電流を求めてみる
これを利用するとホイートストンブリッジの検流計に流れる電流を求めることもできます。
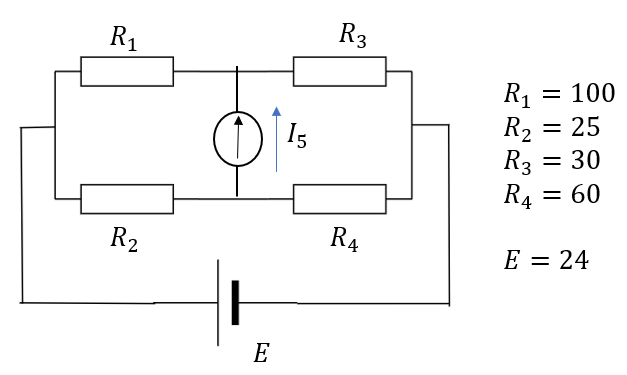
このような回路で検流計の電流\(I_5\)を求めてみます。
ホイートストンブリッジについてはこちらを読んでくださいね。
求めたい電流の領域を切り取る
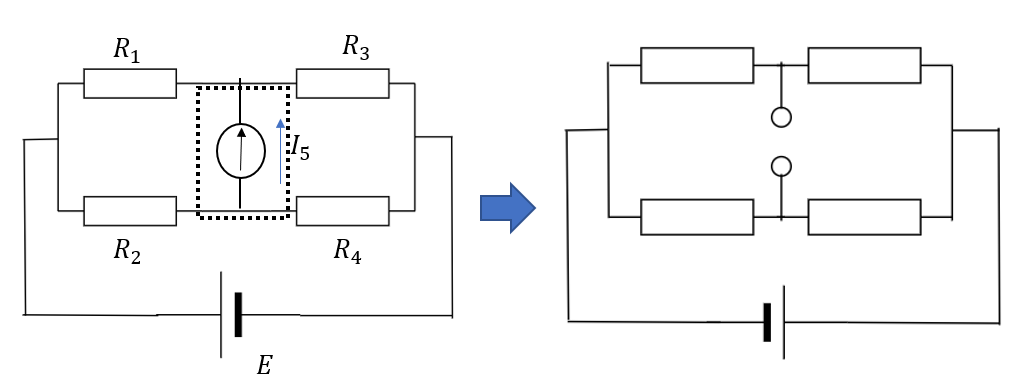
検流計の部分を切り取ります。
切り取った部分の電位差を求める
次に切り取った部分の電位差\(V_{AB}\)を求めます。
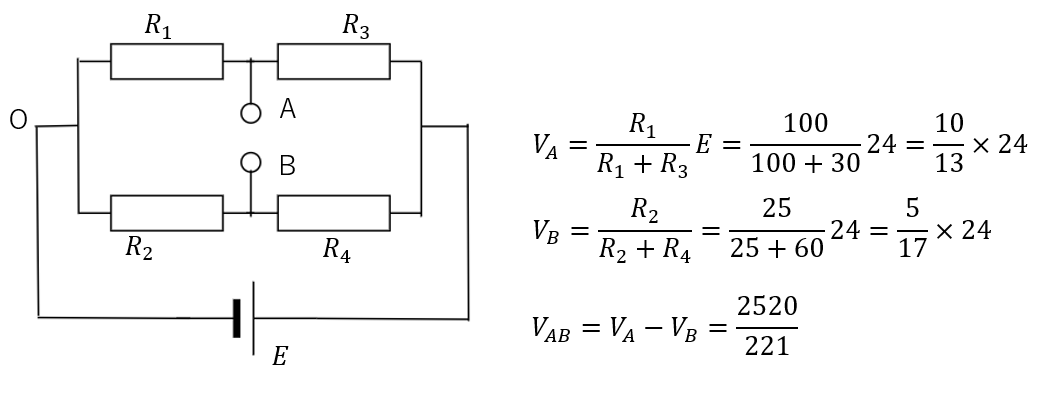
点Oを基準して各電位\(V_A,V_B\)を求めてその差を取れば電位差が求まります。
元の電源を外して合成抵抗を求める
次に元の電源を外して合成抵抗を求めます。
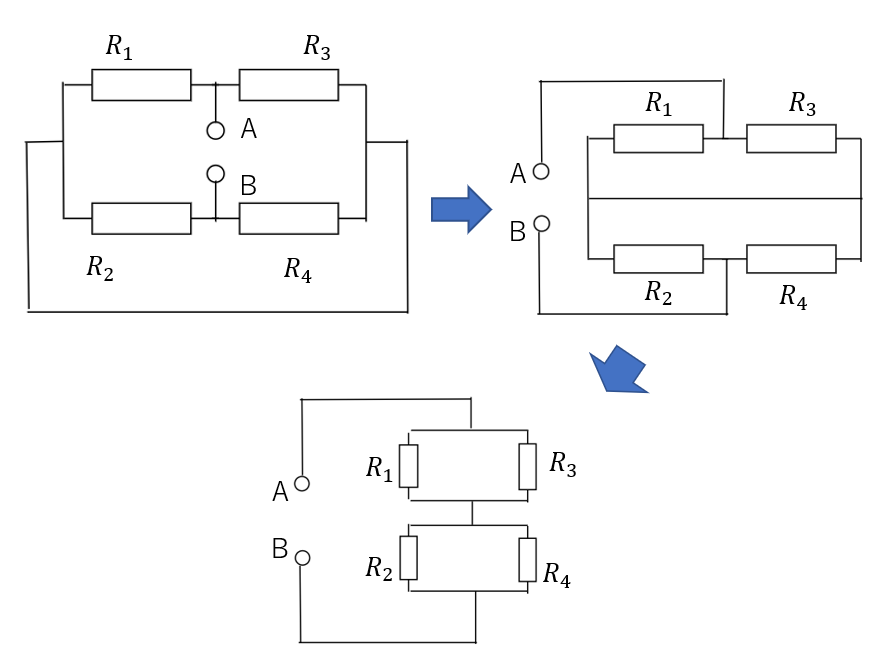
まず電源を外して、ABを電源としたときの回路を作ります。
このままだと見にくいので図のように回路を見やすくします。
最後の図を見れば合成抵抗を求められますね。
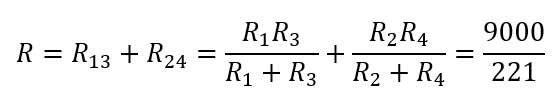
1,2,3の抵抗と電池を直列につなぐ
先ほどと同様につなげばOKです。
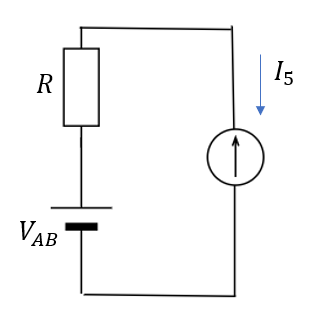
この\(I_5\)を求めれば検流計に流れる電流が求まります。
簡単ですね。
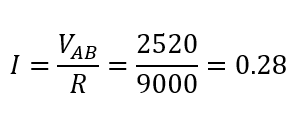
この例では検流計の抵抗を無視しているのでキルヒホッフの法則でも簡単に求められます。
しかし、検流計の抵抗を無視できない場合はこのテブナンの定理を使った方が圧倒的に速いです。
検流計の部分を抵抗ごと抜き取れば、STEP3までは同じで、最後のところで付け加えるだけです。
実際はテブナンの定理は使わない

ここまでテブナンの定理の紹介をして申し訳ありませんが、テブナンの定理は基本的に使いません。
大学入試レベルでは複雑と言ってもキルヒホッフの法則で十分計算できる問題ばかりです。
また、テブナンの定理は特定の電流しか求められません。
入試問題では基本的にすべての電流を考える必要があるのでテブナンの定理の使い道はかなり限定されます。
しかし、計算が早くなり別の問題に時間をかけられるので知っておいて損はないと思います。
まとめ:テブナンの定理の4ステップ

いかがでしたか?
これはあくまで応用の話です。
まずはキルヒホッフの法則を完璧に使いこなせるようにしましょう。
テブナンの定理の使い方
- 求めたい電流の領域を切り取る
- 切り取った部分の電位差を求める
- 元の電源を外して合成抵抗を求める
- 1,2,3の抵抗と電池を直列につなぐ
*特定の電流を求めたいときに使う









