「一つの系見る」(質点系)とは?2物体を扱うときの裏ワザを教えます

どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
物理の問題を解いていたら「一つの系で見ると」や「一つにまとめて考えると」という解説があったんですが、意味が分かりません!
 リケジョ志望のAIさん
リケジョ志望のAIさん
「1つの物体として見る」「一体化する」という言葉を問題の解説で見たことありませんか?
なんとなくイメージはわかるけど、正確な意味が分からないし使い方もよく分からないと悩んでいませんか。
それは当たり前です。学校ではこの詳しい説明って教えてくれませんから。
この「一体化」の正確な意味が分かれば自然と使い方も見えてきます。
この記事では、「物理の系」の中の「1つの系として見る」を解説します。
最後まで読むことで、物理の複雑な問題も解けるようになり、ライバルと差を広げられます!
「物体を一つとして見る」の意味がわかる
入試レベルの複雑な問題が解ける
目次
1つの系で見る(物体を一体化)するとは?

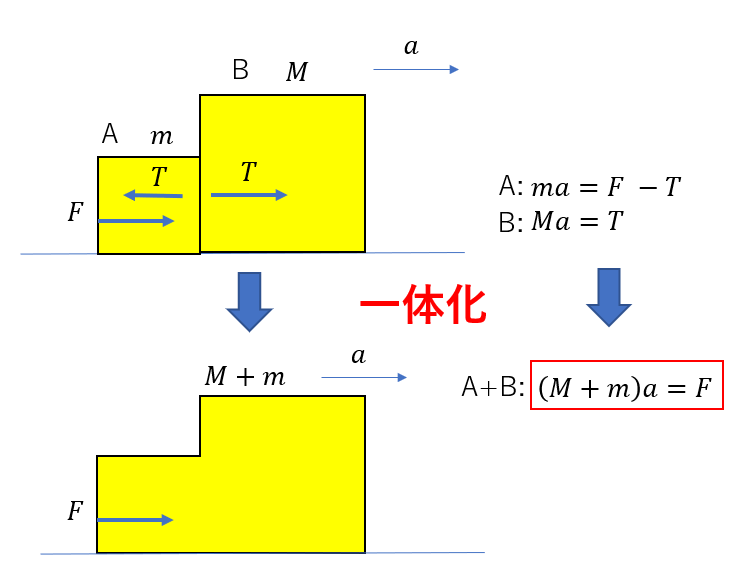
例えば図のように、二物体が接していてAに右向きの大きさ\(F\)の力を加えます。
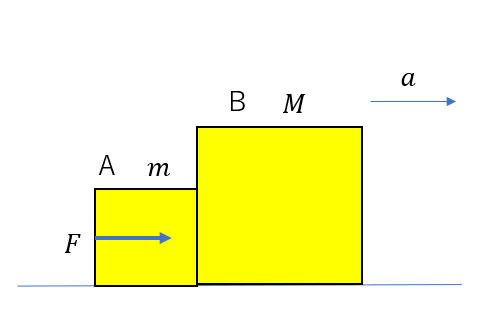
この時に加速度を求める場合、基本は2物体それぞれの運動方程式を立てて求めますね。
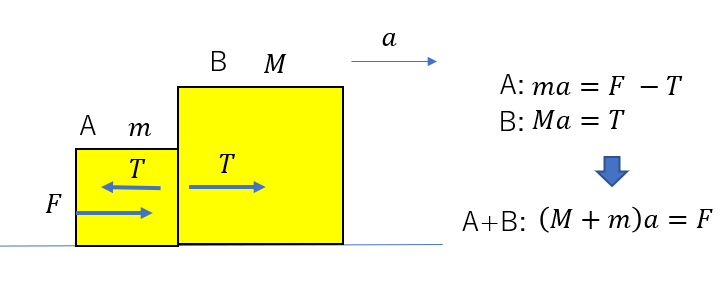
ここで、AとBの運動方程式を足した式(A+B)がきれいな形になっていますね。
これは質量が\(m+M\)の物体に合力\(F\)がはたらいている場合と同じ式になっています。
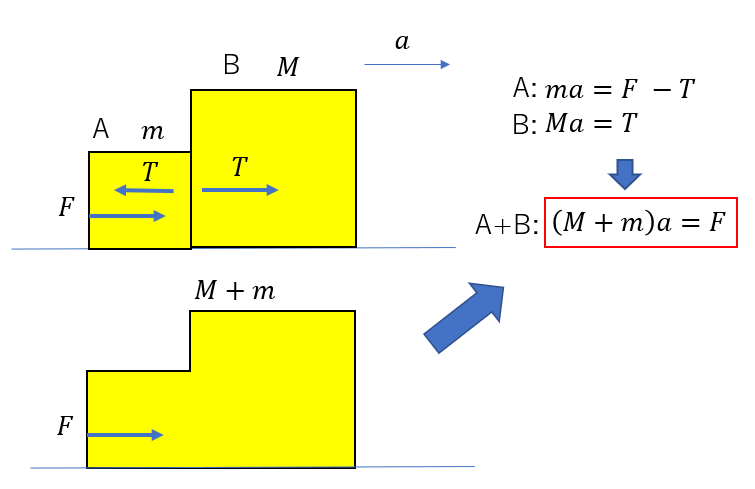
まさにAとBを一体化して見た場合ですね。
1つの系で見ると内力が打ち消される

先ほどの例では互いに及ぼしあっていた力(内力)が打ち消されていました。
一体化すると内力が打ち消されることが予測できますね。
もう一つ例を見てみましょう。
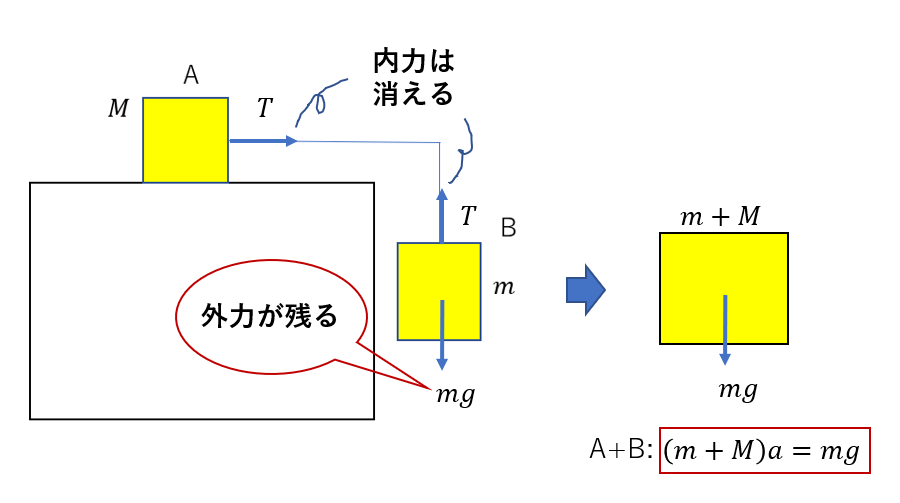
質量\(M, m\)の二つの物体A, Bがあり、図のように、二つの物体は軽い糸でつながっている。摩擦力は無視するとして、この二つの物体の加速度の大きさを求めよ。ただし、重力加速度の大きさを\(g\)とする。

これもまず、A,Bそれぞれの運動方程式を立ててみます。
これは運動方程式を立てていきます。
今回は、A,Bの加速度の大きさは等しいので、加速度の大きさを\(a\) , 張力の大きさを\(T\)と置くと、それぞれの運動方程式はこのようになります。
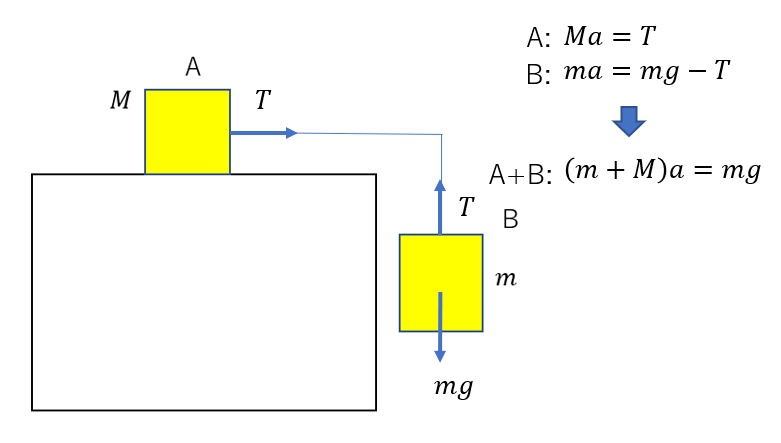
先ほどと同じで、AとBの式を足すと質量が\(m + M\)と一体になって、糸の張力(内力)が打ち消されていますね。
一つの系で見る=式を足す

2つの例を見て分かったかと思います。
この2式を足す操作が、一つの系で見るということなんです!
物体を足し合わせることと式を足し合わせることがリンクしているのが分かります。
イメージと式がリンクしているのは物理の面白いところですね。
一つの系で見たときの運動方程式

式を足し合わせることで内力が打ち消されているのが分かりますね。
これは内力は必ず作用反作用の関係にあるからです。
そして、残るのは外力のみとなります。
一般的に1つの系で見たときの運動方程式は次のように表せます。
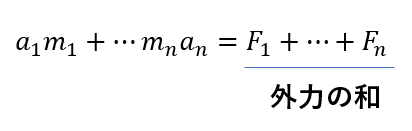
「各物体の運動方程式の左辺\(ma\)を足したものが外力の和に等しい」
このようになります。
一体化したときの運動方程式の使い方

ですが、これではあまり使い勝手がよくありません。
ですがある条件を加えると力を発揮します。
それは加速度の大きさがすべて等しいときです。

このように加速度の大きさが等しいと、1つの物体について立てた運動方程式と同じ形になります。
これなら使い勝手がよさそうですね。
注意1:右辺は一体化前の外力の和です
この式を使う注意点を1つだけ教えます。
先ほどの糸でつながった物体を見てみましょう。

1つの物体として考えるから、右辺を\((m + M)g\)としてしまうミスが多いです。
右辺はあくまで一体化する前の外力の和なので注してください。
この場合はBにはたらいていた重力の大きさ\(mg\)です。
もちろん内力も書いちゃダメですよ。
注意2:加速度の向きを正にする
これは後でやる問題演習のところで詳しく説明します。
物体の運動方向がバラバラの場合、外力の合力を求めるのに注意が必要です。
加速度の向きを正にして考えるので、外力がその向きと逆にあればマイナスをつける必要があります。
1つの系のエネルギー保存則

運動方程式に関して見てきましたが、エネルギーについても同じことが言えます。
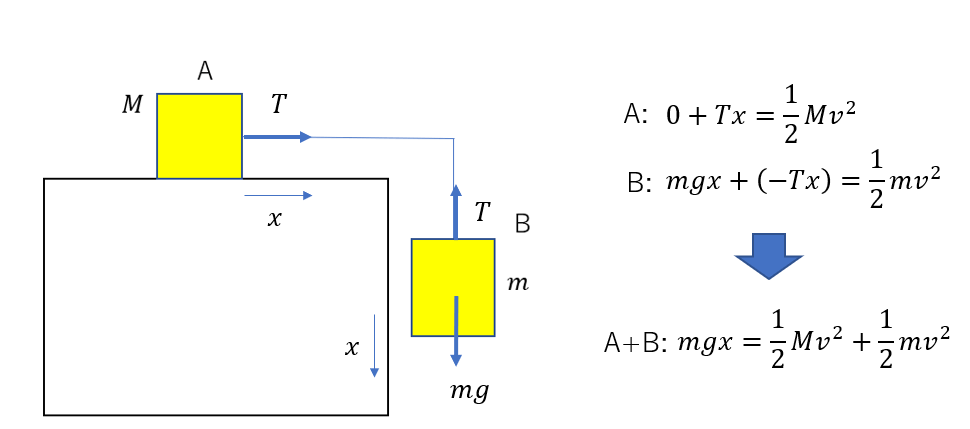
先ほどの糸でつながった2物体について考えます。
AとBが静止した状態から、距離\(x\)だけ動いて速さ\(v\)になったとします。
AとBそれぞれについてエネルギー保存則を立てると図のようになります。
(エネルギー保存則についてはこちらを確認してください)
AとBのエネルギー保存の式を立てると、足すことによって内力がした仕事は打ち消されます。
一般に1つの系で見たときのエネルギーエネルギー保存則は次のように表せます。

式の形は1つの物体で考えた場合と同じです。
ポイントはエネルギーは総和であること。そして、非保存力かつ外力の仕事を考えるということです。
先ほどの例もこれにしたがっています。
1つの系を使うメリット

この1つの系は必須ではありません。
見ての通り、1物体に関して式を立てていけば解けますし、その方が確実です。
しかし、1つの系で考えることで式が複雑にならず、一発で答えを出すことができます。
時間短縮にもなるのでその分別の問題に時間をかけることができます。
1つの系を使った問題
では最後1つ問題演習をしましょう。
水平な机の上に直方体の物体Aをおき、その上に直方体の物体Bを置く。Bには物体Cが、Aには物体Dがそれぞれ糸で繋がれていて、CとDは滑車を通して吊り下げられている。A,B,C,Dの質量はそれぞれ\(2m,3m,m,2m\)である。AとBの間にのみ摩擦が生じる。AとBを静止させた状態から静かに手を放すとBはA上を滑らず、Aとともに左へ運動した。この時、Aの加速度を求めよ。ただし、糸、滑車の質量は無視する。
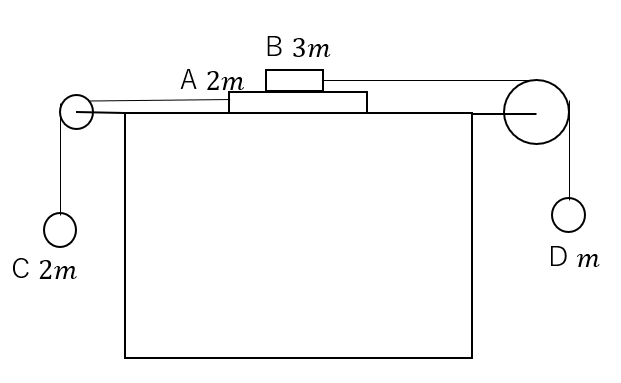
1つの系を使った問題解説

この問題はもちろん運動方程式を考えれば解けます。
しかし、その場合4つの式が必要になってかなり面倒です。
問題文から加速度の大きさはすべて同じだと分かりますので、物体を一体化して考えてみましょう。
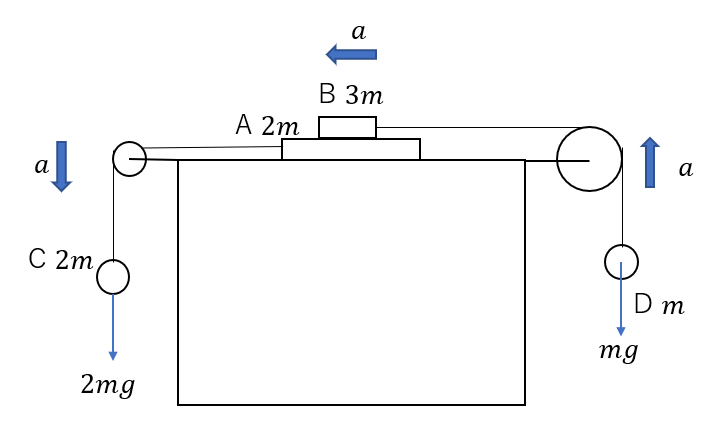
すべての力を書くとごちゃごちゃするのでここでは外力だけ書いています。
もちろん実際にはすべての力を書きだしてください。
後は運動方程式を立てるだけなんですが、一つ注意点です。
先ほどの運動方程式を立てるときの注意点2つ目に関係してきます。
1つの系で見た運動方程式は左辺はすべて正で足しています。つまり、各物体の加速度の向きを正にして足しているのです。
なので、外力の符号がその向きによって変わってきます。
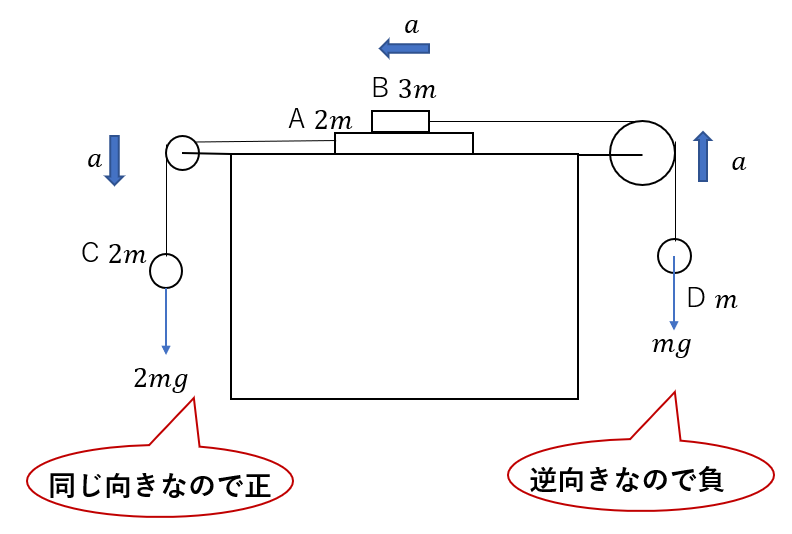
Dについては加速度向きとは逆向きに外力がはたらいてます。
つまり、一体化したときの運動方程式を立てる場合は\(-mg\)として適用しなければいけません。
これが先ほどの注意点2の意味です。
それを踏まえて運動方程式を立てましょう。

このように答えが出せました。
張力と摩擦力は内力だとわかるので、瞬時に答えを出すことができますね。
物理の系は他にもある
この1つの「系」ですが、物理の系にはさまざまなものがあります。
物理の系がそもそも何か?
またどんなものがあるか知りたい方はこちらの記事を見てください。
まとめ:1つの系で見る=式のスケールをでかくする

いかがでしたか?
1つの系ででみることで、式のスケールを大きくしていることが分かりますね。
1つの系でみると式が単純化できますが、運動方程式を正確に立てられない状態でこれを使ってもしょうがないです。
まずは1物体ずつ立てるところからはじめ、慣れてきたらこのような応用テクニックも身に付けても良いですね。
1つの系(一体化してみる)
- 運動方程式

- エネルギー保存則

オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!









