相対速度と相対加速度の公式とその意味とは?

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
相対速度や相対加速度ってどういう意味があるんですか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
今回はこのような悩みを解決していきます。
結論から言うと、相対速度と相対加速度はそれぞれ次のように表されます。
\(\vec{v’} = \vec{v} – \vec{v_0}\)
\(\vec{a’} = \vec{a} – \vec{a_0}\)
これは知っていると思いますが、実はこの「相対」という言葉には高校生の9割がしらない大事な意味が隠されています。
わりと難関大レベルではこの意味を理解できているかで差がつきます。なので、必ず最後まで読んでライバルと差をつけましょう!!
目次
物体を見る方法は無数にある
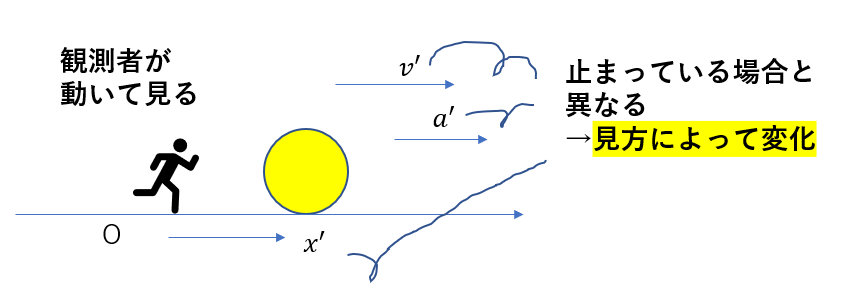
普通は物体を観測するとき、自分は「止まって見る」はずです。そんなこと今まで意識していないと思いますが、「止まって見ている」のです。
ですが、物体の見方というのは別に「止まって見る」だけじゃないですよね。
動いて見てもいいですよね?
観測の仕方は無数にあるんです。
そして、見方によって物理量が変化する場合があるんです
主に、位置、速度、加速度のようなベクトル量は変化します。向きが関係するわけですから、当たり前といえば当たり前です。
止まって見る場合、単に速度\(\vec{v}\)や加速度\(\vec{a}\)と呼びますが、
本当は「止まっている人から見た」速度、加速度なわけです。
人が動いていると、速度も加速度も、そして位置も変化します。
電車とかイメージしてもらうと分かります。自分がホームで待っているときに、電車が通過する速さと自分が電車に乗っていて、逆方向に通過していく電車で見える速さって全然違いますよね。
後者の方が早く感じるわけです。
物理では、こういう「見方」のことを「系」と言います。そして、高校生で知っておいてほしいのが系が3つです。
- 慣性系
- 相対系
- 質点系
慣性系は「止まって見る」ということです。
相対系は今回詳しく見ていきます。
質点系はいわゆる「一つにまとめて見る」という意味です。
たまに、問題集の解説とかで「一つの系で見ると・・・」って書いてあります。これは「質点系」と呼んだりします。
一つの系で見ることは別の記事で説明しています。
では、今回「相対系」についてみていきましょう。
相対速度と相対加速度の公式
まず、相対系を使うと速度や加速度が変化するんでした。
そこで、その動いて見た場合の速度や加速度を導入しましょう。これは相対速度、相対加速度と言います。
ただ、相対系を使う上では、速度や加速度を変化させないといけないんでした。見方によって速度が変わるんでしたね。
これを式に表してみましょう!
物体の床に対する(つまり観測者が止まって見た場合の)物体の速度が\(\vec{v}\)で一定だとする。図のように、観測者が速度\(\vec{v_0}\)で動くとき、観測者から見た物体の速度\(\vec{v’}\)を求めよ。
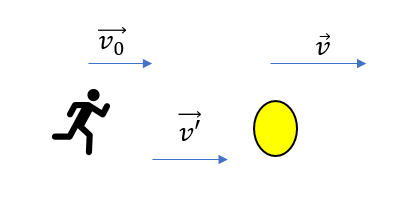
問題にある3つの速度の関係を図にしてみるとこうなります。
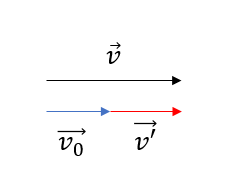
つまり、
\(\vec{v_0} +\vec{v’} = \vec{v}\)
なので
\(\vec{v’} = \vec{v} – \vec{v_0}\)
となるわけです。
これは「観測者から見た物体の相対速度」と言います。
「観測者を基準」にするので、観測者の速度\(\vec{v_0}\)を引く感じですね。
全く同じように、相対加速度も求められます。
\(\vec{a’} = \vec{a} – \vec{a_0}\)
相対速度や相対加速度は運動を簡単にできる(かも)
相対速度や相対加速度の公式は問題ありませんね。しかし、大事なのはこの意味です。
相対速度や相対加速度にはどんな意味があって、問題ではどのように使うのかというのをこれからお話していきます。
これもさっきの電車の例で考えましょう。
ホームで待って通過する電車は当然ですが、高速で通過します。
では、その電車を「全く同じように並走する電車に乗って見る」とどうでしょう。
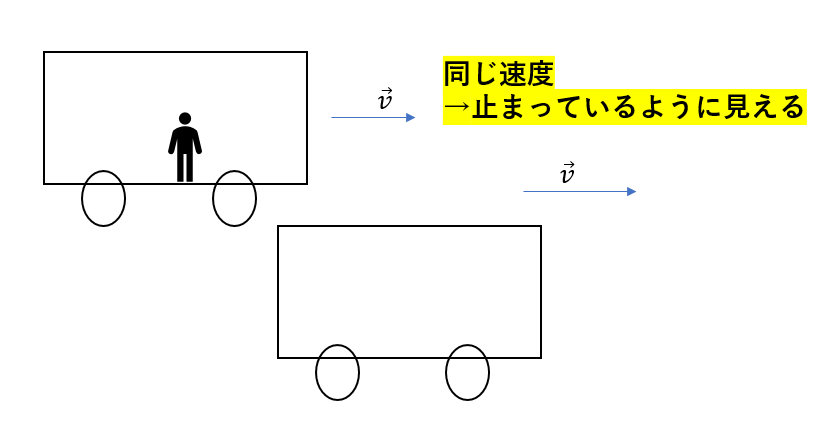
・・・
止まって見えるのがイメージできますね。
動いているのと、止まっているのと、どっちの方がイメージしやすく、簡単ですか?
それは止まっている方ですよね。
こうやってうまく見方を変えると運動が簡単になるんです。
相対系も「止まって見る」の言い換え
そして、もう一つ。
相対系は動いて見るですが、これは「止まって見る」と同じことを言っているんです。
矛盾しているじゃねえか!!って怒らないでください・・・
この考え方は重要なんです。
さっきの例をみてください

観測者から見た物体の相対速度は
\(\vec{v’} = \vec{v} – \vec{v_0}\)
でした。
これは言い換えれば
止まっている人から見た物体の速度が\(\vec{v’} = \vec{v} – \vec{v_0}\)
ということと同じではありません?
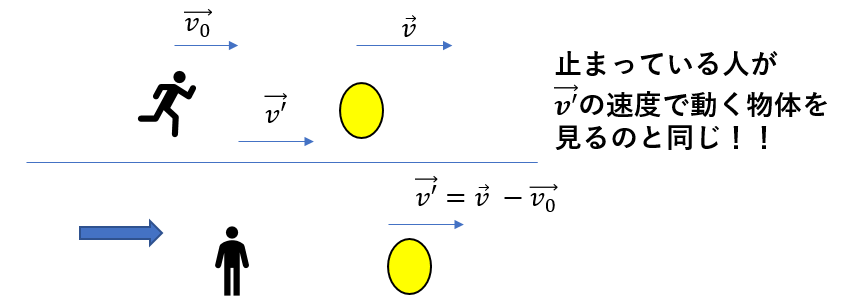
このように、あたかも自分が止まっているように見れるのです。
自分が動いている状態っていうのはどこかイメージしにくいところはありますが、止まっているならイメージしやすいですよね。
こう考えると、相対速度とは「補正した速度」とも見れるわけです。
「自分が止まって見る分、自分の速度を引いて物体の速度を補正してね」ってことなんです!!
相対速度の問題で使ってみよう
では、この考え方を実際に問題で使ってみましょう!
図のように、上面が平らな段差のついた台Cがあり、図に示された位置に、段差と同じ厚さの物体Dが段に接して置かれている。このとき、台Cの上段に面と物体の上面は、一続きの水平面になっている。物体Dの質量は\(M\)であり、物体Dと台Cとの間の摩擦は無視できるとする。ここで、質量\(m\)の小物体が、台Cの上段の面上を運動してきて、速さ\(v\)で物体Dの上面に乗り移り、Dの上面をすべってからDの上で(Dに対して)静止した。重力加速度の大きさを\(g\)、小物体とDの上面との間の動摩擦係数を\(\mu’\)として、次の問いに答えよ。ただし、小物体がはじめに運動していた向きを正とする。
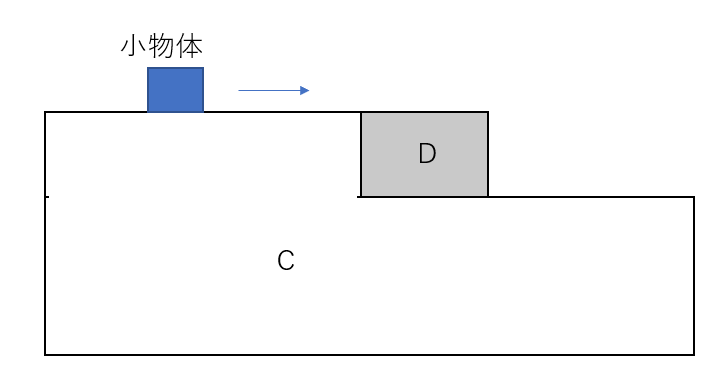
(1) 小物体がDの上を進んでいるときの、Cに対する、小物体とDの加速度をそれぞれ求めよ。
(2) 小物体がDの上を滑り始めてから、Dに対して静止するまでの時間を求めよ
(1)摩擦力の扱いに注意
(1)は運動方程式を立ててあげればいいですよね。
ただ、ここでは摩擦力の扱いに注意してください。
Step 1
まずは小物体から
Step 2
軸は問題文で与えられているので右向きに取ります。
Step 3
力をすべて図示しておきましょう。
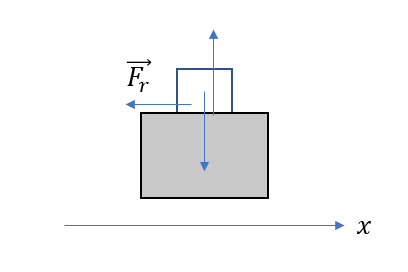
軸方向の力は動摩擦力\(\vec{F_r}\)だけですね。
摩擦力の大きさは\(F = \mu’ N = \mu’mg\)です。
向きは軸と逆向きです。(小物体が移動する向きと逆向き)
というわけで、\(\vec{F_r} = (-\mu’mg)\)
となるわけですね。
Step 4
合力は\(\vec{F} = \vec{F_r} = (-\mu’ mg)\)
です。
Step 5
運動方程式\(m\vec{a} = \vec{F}\)を適用すれば
\(ma = – \mu’mg\)
∴\(a = -\mu’g\)
今回は加速度
を求めるのでこれでOK(大きさじゃないよ!!)
ちなみに、ベクトル量を答えるときは\(\vec{a} = (〇)\)と答えるのは、あっているんですがちょっと怖いので、成分である〇の部分を答えてください!
同じように、Dについても考えます。
ここでの注意点は力の図示です。
Dにも摩擦力が働いているのですが、これは作用反作用の法則にしたがいます。
そもそも、摩擦力っていうのは二物体の接触で起こっているので「〇〇が△△から受ける力」と言い換えることができるんですね。
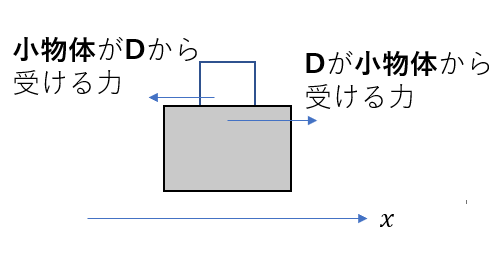
このように、作用反作用の関係にあります。なので、Dが受ける力は
\(F = (\mu’ mg)\) ということです。
なので運動方程式を適用すると
\(Ma = \mu’ mg\)
\(a = \frac{\mu’ mg}{M}\)
となります。
(2)Dに対して静止するとは・・・
(2)が今回の本題です。
二つの物体がどんな運動するかは、見方によって難易度が変わります。
今回はまさにそのパターンです。
止まって見るのでは、イメージがしにくいですよね。
なぜなら、今回
二つの物体が同じように運動していないから!
ただ、あなたは今回武器を一つ手に入れましたね。
そうです「相対系」です。
ここで物体Dに乗って見るとどうでしょう??
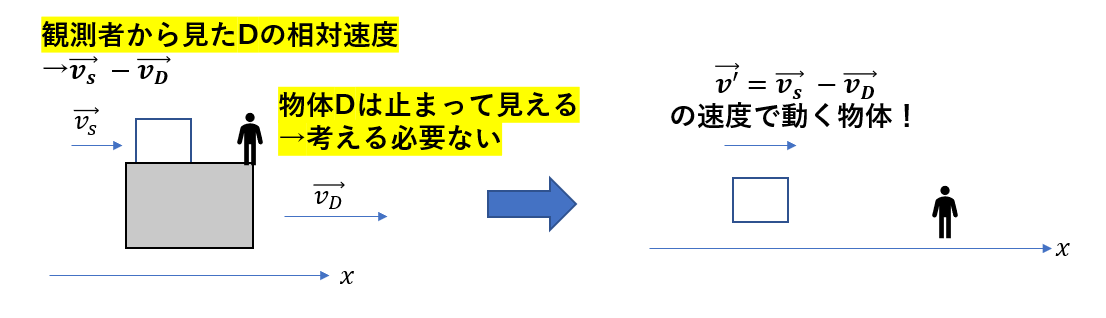
Dに乗って見るということは次の意味があります。
・Dの速度は0→考える必要なし
・小物体の速度は相対速度となる
Dに乗った観測者からみたらDは動いてないですよね。
ですから、この時点でDは考える必要ないんです。
また、相対系では「止まって見る」に置き換え可能でした。
すると、・・・
二物体だったのが一物体の問題に単純化できる!!
一物体なら楽勝ですよね。
小球が静止するのはもちろん\(\vec{v’} = 0\)のとき、つまり
\(\vec{v_D} = \vec{v_s}\)
となるときです。
この\(\vec{v_D} = (v_D) , \vec{v_s} = (v_s)\)は(1)から等加速度運動ってことが分かるので、公式に当てはめれば求められます。
\(\vec{v} = \vec{v_o} + \vec{a}t\)
でしたよね。これに成分を代入していくと
\(v_D = \frac{\mu’ mg}{M}t\)
\(v_s = v – \mu’ gt\)
\(v_D = v_s\)なのであとはtについて解けば終わりです。
\(t = \frac{Mv}{\mu’ g(m + M)}\)
ということでした。
相対系を使うと「二物体」の運動を「一物体」に置き換えることができるんですね。
 AI
AI
そうだね。基本的に、どっちかの物体に乗って見るとうまくいくよ!
 AKINORI
AKINORI
まとめ:相対速度と相対加速度
いかがでしたか?
相対速度と相対加速度の公式だけではなく、その意味も理解できたでしょうか?しっかり復習して理解を深めましょう!
●Aから見たBの相対速度の公式
\(\vec{v_{A→B}} = \vec{v_B} – \vec{v_A}\)
*相対加速度、さらには相対位置も同じ
●相対系の意味
→物体を別の「止まって見る」場合に置き換える
●相対系の使い方
二物体あってイメージがしにくいとき
・どちらかの物体に乗って見る
・乗ってない物体を別の「止まって見る」場合に置き換える
→「二物体」が「一物体」に単純化できる!!
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!










Comment
2物体が異なる運動をしている時には、相対系で見ることで、1つの物体について考えるだけで良くなる。結果、早く解けてミスも減る。
そうですね!かなり応用向きですが、知ってないといけないテクニックですのでしっかり理解してください!
いや、もうマジで物理のエッセンスなんかより全然分かりやすい!!全部読みます!これからも素晴らしい記事宜しくお願いします!
ありがとうございます!どんどん記事を更新していきますね。
もうすぐこのサイトで塾を開く予定です。塾と言っても人数はかなり制限して一人ひとり向き合えるようにしようと思っています。
もし興味がありましたら、直接メールを送っていただけますか?
メルマガの返信でもOKです。