【受験生必見】熱力学の公式と解法を一気にまとめてみた

こんにちは。受験物理Set Upです。
いや、もう多くの人にこのサイトを利用いただけて本当にうれしいです!
 AKINORI
AKINORI
私こそ、こんなにも教えてもらってうれしいです!
 AI
AI
僕は受験生の味方になるべく、このように高校物理の教えているのですが、やっぱりよくある参考書の説明では意味がありません。誰もが物理を得点源にできる。そんなサイトを目指しています。
物理で手っ取り早く点数を稼ぎたいのであれば僕は熱力学を集中してやることをオススメします。
その理由は簡単で、
たった2つのことを意識するだけで、ものの1週間で熱力学の問題で満点を取れる
からです。
え?ほんとですか?
 AI
AI
はい!本気です。マジです。
 AKINORI
AKINORI
僕が大学受験、塾講師、大学の勉強で物理に長く触れてきました。だから分かります。
もうやってること同じじゃん!!
というわけで今回。
熱力学で出てくる重要公式とその使い方、そして解放までをここで一気にまとめちゃいたいと思います!!
受験生は必見ですよ!!
熱力学の二大公式とは?
まず、公式のまとめです。熱力学ではとにかくこの2つの公式を絶対に使ってください。
状態方程式:\(PV = nRT\)
熱力学第一法則:\(Q =\Delta U + W\)
まずこの二つは何があっても忘れてはいけません。
特に第一法則に関しては、それぞれの文字がどのような物理量なのかをしっかり知ることです。
\(W\)は「する」仕事なのか「される」仕事なのか
\(Q\)は「もらう」熱量なのか「放出する」熱量なのか
などなど、文字ではなくどんな量なのかまで理解をしておきましょう。詳しくはこちらに書いてあります。
熱力学で注目するべきことは2つしかない
そしてここからが重要です。はっきり言います。
熱力学の問題は2ステップですべて解けます!
楽勝ですよね。どういう2ステップかというと
- 変化の過程で「一定」を探す
- 公式を適用する
はい、終わりです。楽勝ですね。
本当にこれだけで終わりなんです!!
実際に見てみましょうか。
状態方程式の使い方
そもそも熱力学の問題は「気体の状態を変化させてその様子を追う」というのがテーマにあります。
そして、変化させるには何かしら条件を一定にします。
その「一定」探すのです。
体積0.01m3の密閉容器に温度300Kにした理想気体を入れる。これを圧力一定で温度を400Kに上げた場合、体積はいくらになるか?
例えばこんな問題があったとします。分かりやすいように図を書きます。どんな分野の問題でも図は丁寧に書いてくださいね。
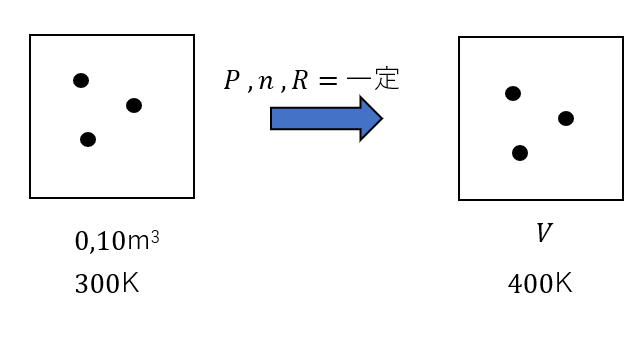
このように分子レベルまで図を書きあげます。
そして、変化の矢印を書いて、その近くに何が一定なのかを書きます。
今回の場合\(P, n ,R\)が一定なのは明らかですね。(この図の書き方はパクってください)
これで「一定」を見つけることができました。
後は二大公式を適用するだけです。今回は状態方程式が一番合っているでしょう。
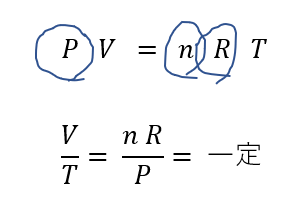
このように、\(P, n ,R\)は一定なのでこのように式変形すると・・・
\(\frac{V}{T} = 一定\)
という関係が現れますね。\(\frac{V}{T}\)は変化前後でイコールなんです。
なので、変化前後の値を代入してイコールで結べばいいんです。
超簡単ですよね。状態変化は何回も起こるものもあればグラフで表される場合もあります。でもやることは同じです。
「一定」を探して公式を適用するだけなのです!!
↓もっと詳しく知りたい方はこちら↓
第一法則の使い方
この「一定」を探して公式を適用する方法はもちろん第一法則でも全く同じです。
容積が変化しない密閉容器に単原子分子理想気体を入れる。最初の状態では圧力、温度、体積は\(P_0, V_0, T_0\)である。気体に熱を加え、温度を\(T_1\)になったとき、気体が得た熱量を求めよ。
もちろんまずは図を書きます。
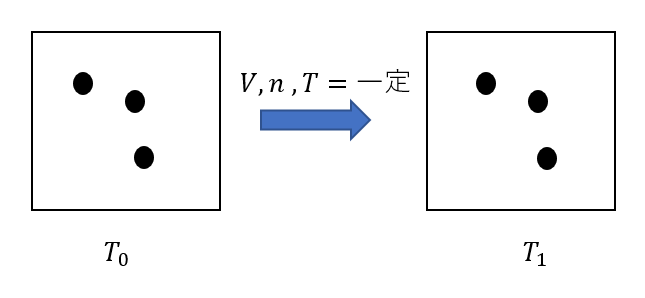
そして、一定を探すわけですが、今回は「容積不変の密閉容器」がポイントです。
容積不変→体積が一定
密閉容器→物質量が一定
ですね。つまり、\(V,n, R= 一定\)となります。
「一定」を探すことができたので公式を適用します。熱量を求めたいので第一法則を使うのがベストですね。
\(Q = \Delta U + W\)
これですが、\(V = 一定\)という条件から
\(W = 0\)
というのが得られます。体積が変化しなかったら仕事はしませんからね。
また単原子分子であれば内部エネルギーの変化量は
\(\Delta U = \frac{3}{2}nR \Delta T = \frac{3}{2}nR(T_1 – T_0)\)
と表すことができるわけです。
つまり
\(Q = \frac{3}{2}nR(T_1 – T_0)\)
となります。
やっぱり「一定を探して公式を適用する」。これだけで解くことができました
もっと詳しい説明はこちらです。
とにかく徹底しよう
いかがでしたか?
とにかくこれを徹底してください。
「一定を探して公式を適用する」
変化が複雑になるほどこの方法は力を発揮します。
一つ一つ確認しながらこの2ステップを踏むことで必ず熱力学は突破できるのでこれを徹底して問題に取り掛かってください。









