熱力学第一法則とは？お金で考えてわかりやすく解説します
熱力学第一法則がエネルギー保存則だと分かる
熱力学第一法則を忘れない覚え方を知れる
「した仕事」「された仕事」の２パターンある理由が分かる
問題での使い方が分かる
あの。熱力学第一法則ってあるじゃないですか？あれちょっと覚えにくいんですけど、どうしたらいいですか？覚えないといけませんか？
AI
熱力学第一法則は残念ながら覚えないといけないね。でも、言い覚え方を知ってるから紹介してあげるよ！
AKINORI
熱力学には完璧に使いこなせなければいけな二大公式があります。
- 状態方程式
- 熱力学第一法則
これです。今回はその一つである熱力学第一法則を学んでいきましょう
熱力学第一法則はなんのことはありません。力学でやった仕事とエネルギーを熱力学バージョンにしたものです。
正直な話
クソ簡単です。
だってお金と同じなんですもの（笑）
ということで、僕が
「熱力学第一法則とは？」というところを超わかりやすく解説し
絶対に忘れない覚え方を
ここで見せていきます！！
↓状態方程式についてはこちらで↓
目次
熱力学第一法則＝エネルギー保存則
まず言いたいのは
熱力学第一法則はエネルギー保存則
です。
そうなんですか！？
AI
そう。だから、力学でやったエネルギー保存則を使って熱力学第一法則を導きたいと思います。
AKINORI
エネルギー保存則についてはこちら↓
こんな状況を考えていきます。
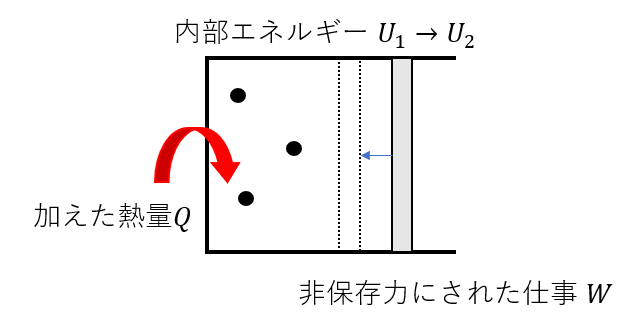
今、理想気体があって、滑らかに動くピストンが付いた容器に入っている。気体には熱量\(Q\)を与え、外部から\(W\)の仕事をされる。この変化によって気体の内部エネルギーは\(U_1\)から\(U_2\)に変化した。それぞれの物理量の関係式を立てよ。
熱量とか内部エネルギーとかなんですか？
AI
その二つを補足しておこうか
AKINORI
内部エネルギーは「力学的エネルギー」
まず気体の「内部エネルギー」です。
これは「力学的エネルギー」だと思ってくれて大丈夫です。
気体は多くの分子が飛び交っているので、運動エネルギーがありますね。また、それ以外にも分子間の静電気力による位置エネルギーもあります。
内部エネルギーについては別のところでお話するので、とりあえず気体がもつ「力学的エネルギー」という認識で問題ないです。
熱量も「エネルギー」
次に熱量ですね。
これはエネルギー（もしくは仕事）の一種だと思ってください。
運動エネルギー、位置エネルギーと同じように「熱エネルギー」ということですね。
つまり熱量を与えたらエネルギーが増えるということです。
これは仕事と同じことですよね。
仕事をすればエネルギーが増える
そういう意味では、熱量は仕事と見てもいいわけですね。
じゃあ、本題に入ろう！！
AKINORI
もちろんエネルギー保存則を使いたいんです。
エネルギー保存則はこうでしたね。
（はじめの力学的エネルギー）＋（非保存力にされた仕事）
＝（あとの力学的エネルギー）
これを使うために情報収集します。
- はじめの力学的エネルギー・・・\(U_1\)
- 非保存力にされた仕事・・・\(Q + W\)
- あとの力学的エネルギー・・・\(U_2\)
補足した通り、内部エネルギーは力学的エネルギーのことですから、
はじめ（あと）の力学的エネルギーは\(U_1\)や\(U_2\)です。
また、非保存力にされた仕事では\(W\)以外に熱量があります。熱量を与えるってことは「仕事をされる」というのと同じな\(Q\)も「非保存力にされた仕事」に含みます。
あとは適用するだけです。
\(U_1 + (Q + W) = U_2\)
∴\(Q + W = U_2 – U_1\)
さて、右辺を見てみましょう。
あ！「後－前」の形だからこれは変化量ですね！！
AI
そう！なので\(\Delta U = U_2 – U_1\)とおこう
AKINORI
内部エネルギー変化量を\(\Delta U\)としておけば
\(\Delta U = Q + W\)
あ！私が知ってる式だ！
AI
これが熱力学第一法則です。こうやってエネルギー保存則から導けるんだね
AKINORI
これがよく教科書とか問題集のまとめに書いてある形です。
もちろんこれでもいいんですが、ちょっと変えます。
式変形して
\(Q = \Delta U – W\)
この\(W\)は気体がされた仕事ですね。
つまり、\(-W\)は気体がした仕事です。
なので、\(-W\)を気体がした仕事として改めて\(W\)と置き換えると
\(Q = \Delta U + W\)
こっちを熱力学第一法則としましょう。
＊このサイトではこっちを使います！！
今の状況では\(Q\)はもらった熱量ですよね。じゃあ、失ったらどうなんですか？
AI
その時はマイナスにすればいいよ！
AKINORI
あくまでこの第一法則で使っている文字の意味は
\(Q\)：もらった熱量
\(\Delta U\)：内部エネルギーの変化量
\(W\)：気体がした仕事
です。
\(Q\)については、失ったらマイナスになります。
\(\Delta U\)は変化量なので、どんなことがあっても「後－前」で表します。なので、当然マイナスになる場合もあります。
\(W\)はここでは気体がした仕事なので、された場合はマイナスになります。
このように、正負が関係するので注意してください。
- 熱力学第一法則
\(Q = \Delta U + W\)
＊注意
\(Q\)：もらった熱量 → 失ったらマイナスにする
\(\Delta U\)：内部エネルギーの変化量 → 絶対「後－前」なのでマイナスのこともある
\(W\)：気体がした仕事 → されたらマイナス
内部エネルギーと仕事について
ここで、仕事と内部エネルギーを具体的に式にしてみます。
気体のした仕事
これは純粋に定義から考えましょう。
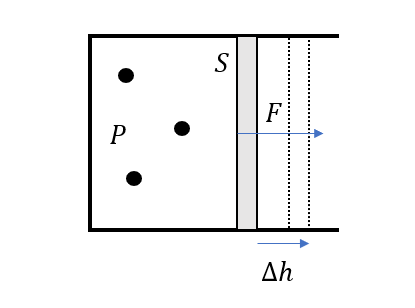
圧力が一定で、断面積\(S\)のピストンを\(\Delta h\)だけ押し出します。
この時の気体のした仕事を考えましょう！！
まず気体がピストンを押す力の大きさを考えましょう。
これは
\(F = PS\)
ですね。
今回、圧力\(P\)も断面積\(S\)の一定なので、力の大きさ\(F\)も一定です。
なので仕事は「力×距離」で求められます。
\(W = PS\Delta h\)
さて、このうち\(S\Delta h\)に注目すると・・・
「底面積×高さ」
つまり、下の図の体積ですね。
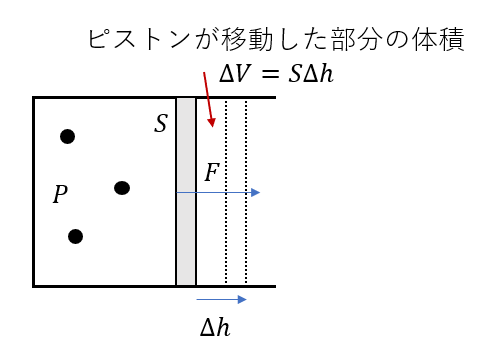
つまり、体積の変化量です
\(\Delta V = S\Delta h\)
と置けば
\(W = P\Delta V\)
これが気体のした（された）仕事です。
「力×距離」
と比較すると関連がありますね。
今までの仕事は「物体一個」を考えていたけど、今は「気体」というたくさんの分子を考えています。
ですから力や距離といった物理量を気体スケールに変えればいいわけです。
もちろん、「圧力×移動体積」と書けるのは圧力が一定のときだけです。
圧力が一定じゃないとき（一定のときでも）仕事は
P-Vグラフの面積で出せます。
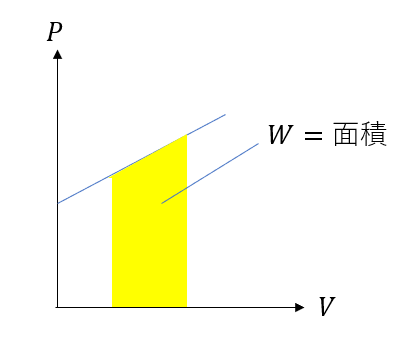
熱力学ではグラフを使った問題がかなり出ます。
なので、グラフから求めるやつは結構お世話になるので頭に入れておいてください。
内部エネルギー
これは、別の記事で説明します。結論だけ言うと
単原子分子理想気体の内部エネルギー
\(U = \frac{3}{2}nRT\)
熱力学第一法則はお金で考えよう！
Akinoriさん。熱力学第一法則はわかったんですが、なんでわざわざ式を変形したんですか？
AI
それは、今変形したような形の方が理解しやすいからなんだ。この式は「お金」に例えることができるんだよ。
AKINORI
おかね・・・？（私大好き！！）
AI
もう一度、第一法則を確認しましょう。
これをお金に例えてみましょう。
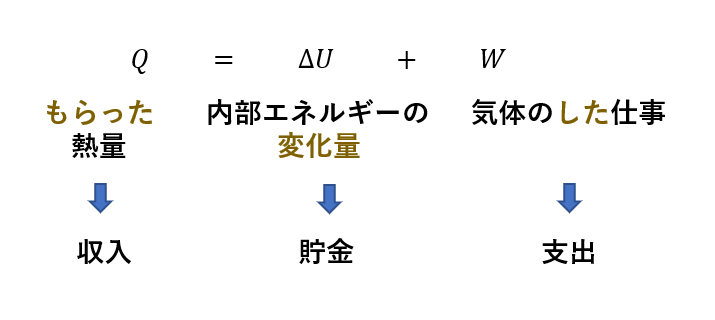
熱力学第一法則っていうのはつまり・・・
「もらったお金\((Q)\)を貯金するか\((\Delta U)\)使うか\((W)\)」
っていう単純な関係を表しているだけなんですね。
うわ！面白い！！覚えやすい！！私はもらったお金はすぐ使っちゃうから\(\Delta U = 0\)かしら（笑）
AI
AIさん。それがまさに熱力学第一法則の使い方につながるんだ！（まあ、貯金はちょっとしてほしいけど・・・）
AKINORI
ということで、この熱力学第一法則の使い方を別の記事で紹介します！！
まとめ
- 熱力学第一法則
\(Q = \Delta U + W\)
「もらったお金\((Q)\)を貯金するか\((\Delta U)\)使うか\((W)\)」
・\(W = P\Delta V\)（P=一定）
・\(U = \frac{3}{2}nRT \) \((\Delta U = \frac{3}{2}nR\Delta T)\)
＊注意
\(Q\)：もらった熱量 → 失ったらマイナスにする
\(\Delta U\)：内部エネルギーの変化量 → 絶対「後－前」なのでマイナスのこともある
\(W\)：気体がした仕事 → されたらマイナス
↓熱力学第一法則の応用法もチェック↓
