熱力学の状態方程式を徹底理解!3ステップで問題も楽々解ける

この前やった状態方程式の使い方、すごかったです。でもあれだけで本当に解けるんですか?
 AI
AI
解けます!ある程度はね。もちろん、別に使う公式もあるけど、状態方程式が使えれば基本はOKだよ。今日は問題を解いてみようか
 AKINORI
AKINORI
というわけで、状態方程式を使って問題を解いてみましょう。
とその前に二つ注意点があります。
「一定」を探すときの注意点
その前に一つ確認しておきたいことがあります。
- 図を書く
- 「一定」を探す
- 状態方程式を「左辺=一定」の形にして適用
この2番目の「一定」ですが、
この「一定」が問題文に直接書かれていない場合も結構あるんです。
「圧力を一定にして・・・」
のような直接的な説明が問題文に書かれてない可能性があるんです。
え?じゃあ、どうしたらいんですか?
 AI
AI
問題文には直接的ではないけど、「一定」を表すような言葉があるんだ。それを探せばいいよ
 AKINORI
AKINORI
例えば、「密閉容器」であれば分子の出入りがない、つまり分子数が変化しないから
\( n = 一定\)ですね。
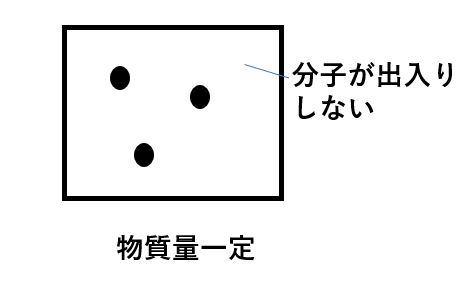
他にも「一定の容積」とかだったら
\(V = 一定\)
となります。
このように、言ってることは同じだけど違う表現で表せることも多いんです。
その表現を式で考えるようにしてください。
圧力は「ピストンのつり合い」で求められる
そして、もう一つ。
\(PV = nRT\)
の物理量で
まず\(P\)を求めさせられる場合がよくあります。
というのも、\(P\)は
ピストンのつり合い
で求められるからです!!
確かに僕は「状態方程式を使えればOK」とは言いましたけど、絶対ではないです。
状態方程式では圧力が求められないときに、他の手段が無かったら詰みますね。
ということで、圧力が「ピストンのつり合い」で求められることは覚えておいてください。良く問われます。
んで、それをどう求めるかというと、例えば図のような場合。
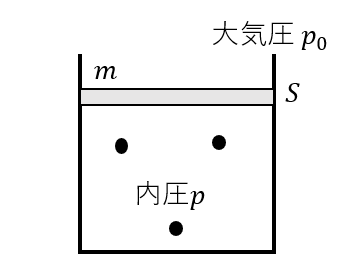
大気圧が\(p_0\)、ピストンの質量が\(m\), 断面積が\(S\)の場合の内圧を求めたい。
という場合。
状態方程式を使うには\(T, V, n\)の情報が無いので求められないですね。
こういうときにピストンのつり合いを考えます。
圧力は、「1m2当たりの力」つまり、
\(p = \frac{F}{S}\)
と表されます。
これを用いれば、気体が押す力の大きさが求められます。
\(F = pS\)
ですね。
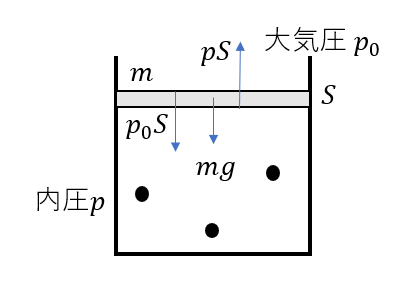
図のように
- \(p_0S\) ・・・大気が押す力の大きさ
- \(pS\)・・・内部の気体ア押す力の大きさ
- \(mg\)・・・重力
この力を使って力のつり合いをたてることができます。
\(pS = p_0S + mg\)
∴\(p = p_0 + \frac{mg}{S}\)
こうやってピストンのつり合いから圧力を求められることも知っておいてださい。
では、実際に問題を解いてみましょう!

問題
図のように、円筒形の容器が、なめらかに動くピストンによって、A,Bの二つの部分に区切られている。はじめA,Bの気体はともに圧力\(p_0\)、温度\(T_0\)であり、容器の底からピストンまでの長さはともに\(L\)であった。Aの気体の温度を\(T_0\)に保ったまま、Bの気体の温度を\(T (T_ 0< T)\)にすると、ピストンはどちら側にどれだけ移動するか。
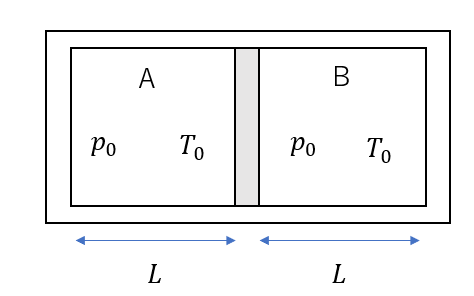
(セミナー物理基礎・物理 2016, 問283)
ではいきましょう。
もちろん、状態方程式を立てるんですが、手順をもう一度確認しましょう。
- 図を書く
- 「一定」を探す
- 状態方程式を「左辺=一定」の形にして適用
じゃあ、図を書いてみます!
 AI
AI
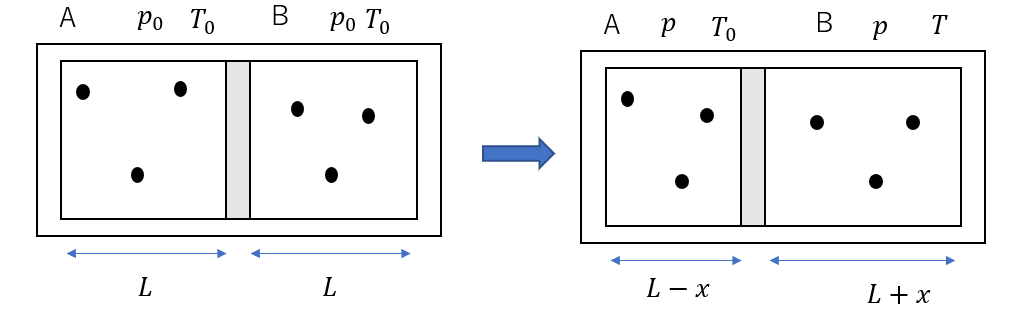
こんな感じですね。
まず、ピストンがA側に\(x\)だけ動くと考えて、この\(x\)を求めにいきます。
え~と、変化後の圧力はなんでA,Bで同じなんですか??
 AI
AI
これはさっき見た「ピストンのつり合い」からわかることだよ。
 AKINORI
AKINORI
変化後のピストンのは静止していますね。
ということは、力がつり合っています。
A,Bの圧力をそれぞれ\(p_A, p_B\)としてみると
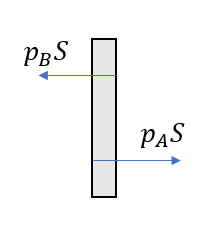
ピストンに働く力はこうなります。
これのつり合いを考えれば
\(p_A = p_B\)
ですね。
ですから、A,Bの圧力を同じ\(p\)と置いているんです。
なるほど!図が書けたから次に「一定」を探すんですね。
 AI
AI
今回の一定は、
Aについては
- 温度\(T\)
- 物質量\(n\)
Bについては
- 物質量\(n\)
ですね。(気体定数は絶対「一定」なので無視です)
最後は状態方程式を「左辺=一定」にして適用するんでしたね。
 AI
AI
A,Bそれぞれについて状態方程式を考えます。
Aについて
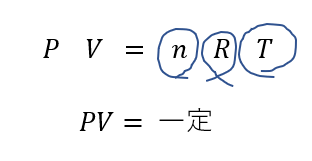
ということなので、変化前後でイコールにすればいいですね。
ただ、体積を\(V, V_A\)とかで表すと文字が増えて嫌なので、ピストンの断面積を\(S\)とすれば体積は
「底面積×高さ」で表されます。
高さはすでに\(L\)で表されるのでこっちの方が良いですね。
というわけで
\(p_0・SL = p・S(L – x)\)
∴\(p_0L = p(L – x)\)
次に
Bについて
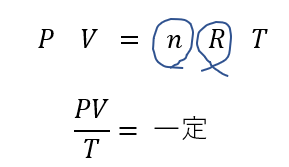
ということなので
\(\frac{p_0・SL}{T_0} = \frac{p・S(L + x)}{T}\)
∴\(\frac{p_0L}{T_0} = \frac{p(L + x)}{T}\)
今、求めたいのは\(x\)です。
んで、\(p\)は自分で設定したものだから、邪魔です。
いらないですね。
なので、\(p\)を消去することを考えましょう。
今求めた二つの式
\(p_0L = p(L – x)\)
\(\frac{p_0L}{T_0} = \frac{p(L + x)}{T}\)
両辺割れば\(p\)が消えそうですね。
なので両辺割って見ると
\(T_0 = \frac{L – x}{L + x}T\)
∴\(x = \frac{T – T_0}{T + T_0}\)
と答えが出ますね。
つまり、答えは
「A側に\(\frac{T – T_0}{T + T_0}\)」
です。
B側に\(x\)と考えた場合は?
これって最初に「A側に\(x\)動く」って考えて解いたじゃないですか?これって「B側に\(x\)動く」って考えてはダメなんですか?
 AI
AI
もちろんOKだよ。でもこの場合、最後の\(x\)の値が負になっちゃうからそこは注意ね。
 AKINORI
AKINORI
もし、最初に「B側に\(x\)だけ動く」と考えると
\(x = \frac{T_0 – T}{T + T_0}\)
という式が得られます。
ただ、問題文では\(T _0 < T\)つまり\(T_0 – T < 0\)なので、この\(x\)は負になってしまうね。
負ということは「逆」という意味。
つまりA側に動くってこと。
なのでこの場合も
「A側に\(\frac{T – T_0}{T + T_0}\)」
が答えになるので、どっちを仮定してもいいです。
けど、ある程度予想しておいた方がいいよ。
今回もBの温度が上がるんだから、ピストンはA側に動くだろうな~
という予想を立てておくといいかもね。
やっぱり状態方程式で簡単に解けるんですね!!素晴らしいです。
 AI
AI
熱力学は「状態方程式」と「熱力学第一法則」っていうのが使いこなせればだいたい解けちゃうので、状態方程式はしっかり使いこなせれるようにしよう!!
 AKINORI
AKINORI
まとめ
- 状態方程式(\(PV = nRT\))の使い方
- 図を書く
- 「一定」を探す
- 状態方程式を「左辺=一定」の形にして適用
- 圧力だけちょっと注意!!
ピストンのつり合いで圧力を求めることも多いよ!!