【高校物理】たったそれだけ！？連結容器の気体の混合問題の解き方
こんにちは。受験物理Set Upです。
気体を混合する問題があるじゃないですか？あれがよくわからないんです。解説もなんか難しくて・・・
AI
物理の熱力学分野では必ず気体の混合の問題をやりますよね？
いくつか問題があるんですが、解説を見るとなぜかどれも違う解き方をしているんですよ。
・混合前後で物質量(mol)は一定
・内部エネルギーは一定
なぜかこの2通りの方法で解いているんですね。もちろんどちらでも解けます。
ですが、全く別の方法で解いているから問題を暗記したりパターン化して「暗記物理」になってしまうんですよね。
そこで今回は、混合気体の問題で絶対に間違えない最強の解き方を教えます。
目次
気体の混合問題
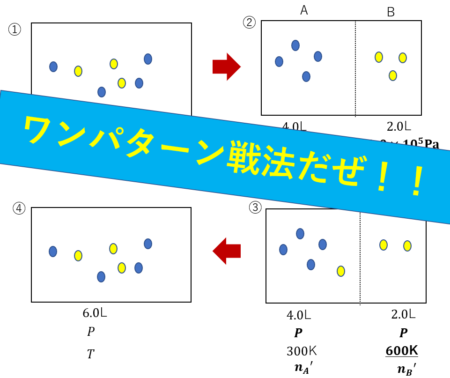
今回はこんな問題を用意しました。
容積が4.0Lと2.0Lの2つの容器A,Bが細い管でつながれ、中井に温度300K, 圧力1.0×105Paの空気が密閉されている。容器Aを300Kに保ち、容器Bの温度を600Kに上昇させると、容器内の圧力は何Paになるか？
（セミナー物理2016 問285）
この問題はセミナー物理から引用しました。その解説はこのようになっています。
・・・なんか面倒そう
AI
そうなんだよね。この問題は比較的計算やすい形になっているけど複雑になることもあり得るよね
AKINORI
特に足し算や引き算は面倒になることが多いんですね。
このような連結容器を使った気体の混合問題は非常に簡単に解く方法があります。
気体を混合しても分離してもエネルギーは同じ
その方法というのが
熱力学第一法則
です。
熱力学では状態方程式と第一法則がすべてですので、これ以外考えられませんね。
熱力学第一法則というものはこういうものです
\(Q = \Delta U + W\)
\(Q\)：吸収した熱量
\(\Delta U\)：内部エネルギーの変化
\(W\)：気体がした仕事
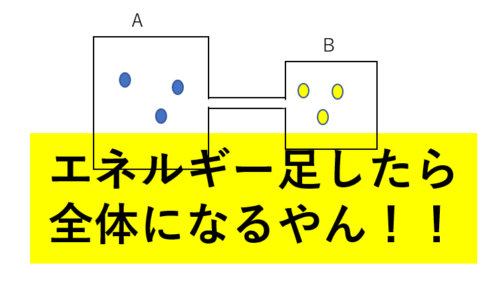
気体の混合や分離をするときは
エネルギーが変化しない
という特徴があります。（熱の出入りが無い場合）
これを使えば一発このような問題は解けます。
そういえば問題でそういう解説みたことあります。でもそうなる理由がいつもわからないんですよね。
AI
だよね。なので、これについて詳しく解説したものがあるから確認してね。
AKINORI
エネルギーを使えば楽々解ける
先ほど紹介した記事では
（混合気体全体のエネルギー）＝（各気体のエネルギーの和）
となるという説明をしました。
これを使えば計算が一気に簡単になり、計算ミスも時間も限りなく減らすことができます。
では実際に解いていきます。
まずは図を書こう
熱力学では必ず、図にしてその中に情報を書き加えていきます。
（細管など細かく図を書くのではなく、状況を変えない程度に簡略化すると良いです）
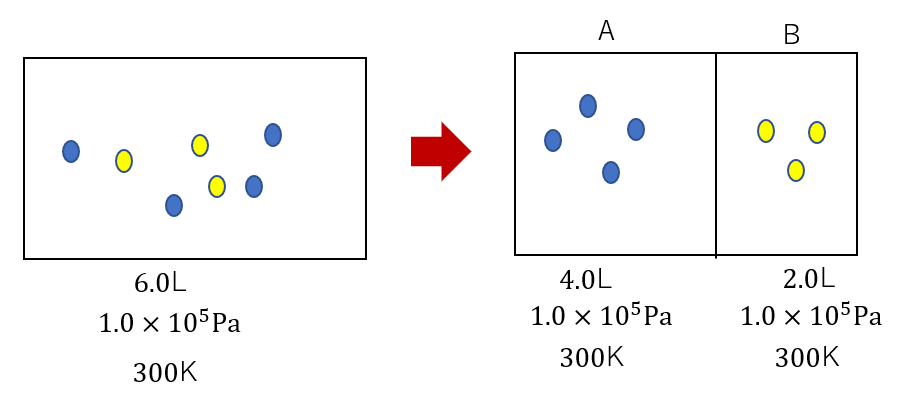
問題文を見ると最初は左側の状態からスタートすることが分かります。
そしてこの問いではAとBの温度を変える操作が行われるので気体をAとBにそれぞれ分離します。
ちなみにこの分離の仕方は受験化学コーチわたなべさんが分かりやすく解説していますので、確認ください。
分離した図が右のようになります。
ここからBの温度を600Kに変化させるのですが、ここが非常に重要になってきます。
問題には主に2通りあって、コックがついている場合とついてない場合があります。
（コックがついている方が実は簡単です）
今回はコックがついていないので、AとBの圧力は常に同じ値で保たれます。
細管を気体分子が自由に行き来できるからです。
それに注意して図を書いていきます。
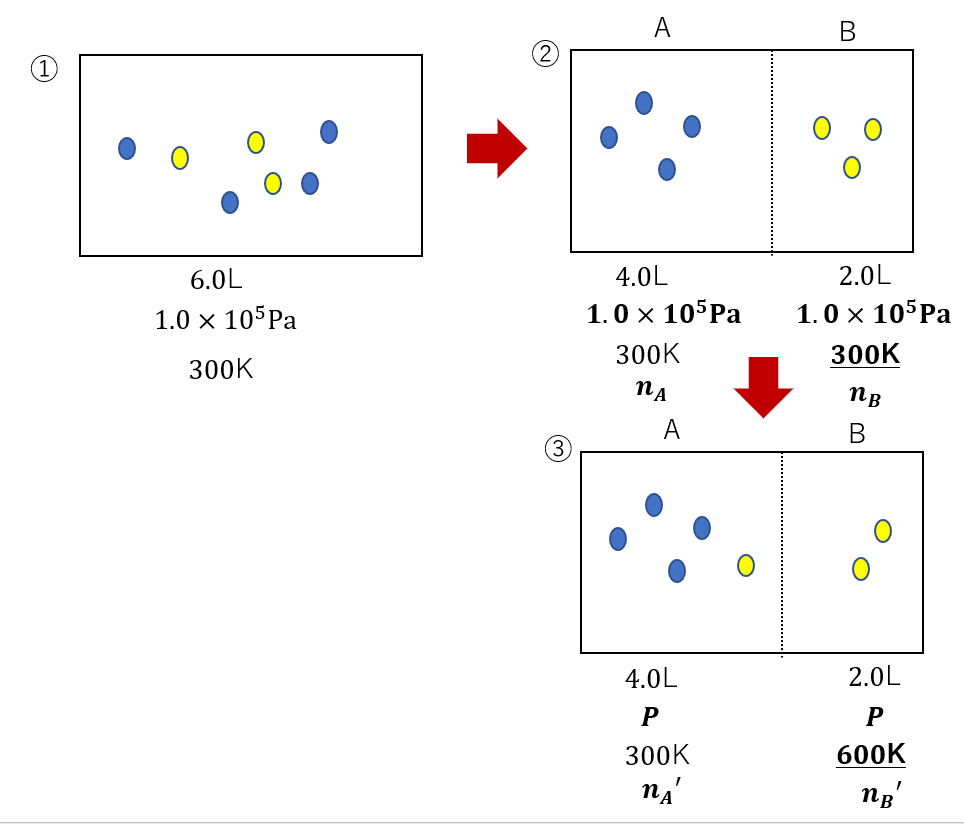
③のように、圧力を\(P\)と同じ値に設定しておきます。
この状態から最後の混合に行きつくわけです。
あとは一つ一つの変化をじっくり見ていけばOKです。
図②について
まずは図②に注目しましょう。この図から物質量\(n_A, n_B\)の関係が分かります。
それぞれについて状態方程式を立てると
\(100k \times 4.0 = n_a R \times 300\)
\(100k \times 2.0 = n_B R \times 300\)
（kはkm（キロメートル）のk（キロ）と同じで\(10^3\)を表します）
この二式から
\(n_A = 2n_B\)
という関係式が得られますね。
元の混合気体（図①）の物質量を\(n\)とすれば
\(n = n_A + n_B = 3n_B\)
となることもOKですね。
図③について
図③でも同様に、\(n_A’, n_B’\)の関係式を導けます。
状態方程式をそれぞれ立ててみると
\(P\times 4.0 = n_A’R\times 300\)
\(P\times 2.0 = n_B’ R\times 600\)
この二式から
\(n_A’ = 4n_B’\)
という関係が成り立ちますね。
物質量の総和は変わってないので
\(n = n_A’ + n_B’ = 5n_B’\)
となるのもOKですね。
図④：「エネルギーの和＝一定」で混合
ここまで来たら後は「エネルギー＝一定」で混合します。
単原子分子とは書かれていないので内部エネルギーは
\(U = \frac{3}{2}nRT\)
とは書けませんが、定積モル比熱\(C_V\)を使って
\(U = n C_V T\)
と一般的に書くことができます。
（混合気体全体のエネルギー）＝（混合前の各気体のエネルギーの和）
ということなので
\(n C_V T = n_A’ C_V \times 300 + n_B’ C_V \times 600\)
\(C_V\)は見事に消えますね。
そして、先ほどの関係式をここに代入して見ると
\(5n_B’ T = 4n_B’ \times 300 + n_B’ \times 600\)
\(T = 360\)
このように\(n_B’\)もうまく消えて混合気体の温度が出せました。
問題集の解答では物質量を具体的に出していましたが、それをうまく回避できていますね。
ここまで来たら楽勝です。
①→④
という変化を見れば
\(V, n R = 一定\)なので
\(\frac{P}{T} = 一定\)
\(\frac{100k}{300} = \frac{P}{360}\)
\(P = 120k = 1.2\times 10^5\)Pa
ということで、無事に解答と同じ結果になりましたね。
私こっちの方がいいかも！
AI
コックがある場合はどうしたらいいの？
今回とは別で、コックがある場合はどうしたらいいんですか？
AI
今回はコックがなく分子が自由に行き来することができるので図③のところで同じ圧力\(P\)としておくことができました。
コックがある場合は特に変わりはなく、図3がAとBで違う圧力になるという違いだけです。
ただこの場合、基本的にAとBの圧力を簡単に求められるような問題設定になっているので、コックなしのときのような物質量を考える手間が省けることが多いです。
コックありの問題となしの問題をそれぞれ解いてみて、どれだけ簡単か体験してみると良いですね。
さっそく問題を解いてみよう
いかがでしたか？
混合問題はコックがある場合と無い場合の二通りしかありません。
コックなしの場合はもう今回見せた問題以外にパターンがありません。
コックありでも同じように解けるので、とりあえず気体の混合問題は絶対に解けます。
今回見せた解法でいろんな問題を解いてみてください。やっていることが同じだと気づけると思います。
それでは。
Comment
いつも有用な物理学習教材をご提供くださいまして、誠にありがとうございます。
「図②について」の式ですが、正しくは
100ｋ×4.0×10^-3=ｎaＲ×300
100ｋ×2.0×10^-3=ｎbＲ×300
ではないでしょうか。
以上、ご確認のほどよろしくお願い致します。
これが成り立つのは容器が断熱材の時だけですか？
紹介ありがとうございます！
こちらこそ、いつもありがとうございます！