気体分子運動論とは？問題必勝パターンを分かりやすく解説
Akinoriさん。熱力学で気体分子運動論っていうのがあるじゃないですか？あれって入試で出るんですか？
AI
もちろん！でもね、気体分子運動論が出たらラッキーだと思ってください！
AKINORI
え？なんでですか？
AI
流れが決まっているからだよ。
AKINORI
気体分子運動論は結構入試でも問われます。
でも安心してください。
気体分子運動論は余裕です！！
ここでやる流れを理解できていればOKです。
なので、今回やることは完璧に人に説明できるようにしてください！！
気体分子運動論とは？
そもそも、気体分子運動論って何？
こんな難しそうな名前付いちゃってるけど何！？
となってしまうので、概要を簡単に説明してから細かい話に入っていきます。
今まで、見てきた状態方程式とか第一法則とかはすべて「気体」という大きな観点から見てきましたね。
でも、「気体」って結局のところ、「分子の集まり」ですよね？
だから、
気体のふるまいを分子レベルでみたらどうですか？？
という提案を受け入れよう！！
というのが「気体分子運動論」です。
要は力学から熱力学へつなげようというお話です。
流れはこんな感じです。
- 分子一個の衝突
- 全分子の衝突
→これにより圧力がわかる！！
- 状態方程式から温度の正体がわかる！？
ではやっていきましょう！！
分子一個の衝突
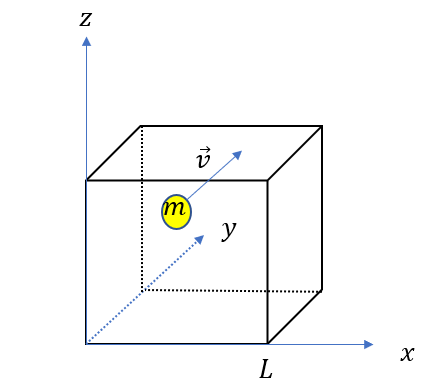
まず、一辺が\(L\)の立方体があって、この中に質量\(m\)の気体分子が\(N\)個入っている状況を考えます。
まず、気体の圧力を考えたいので、
分子一個が壁に衝突する様子を見ていきます。
圧力は簡単な話、「壁を押す力」なので壁の衝突を考えれば圧力は出るだろう、ということです。
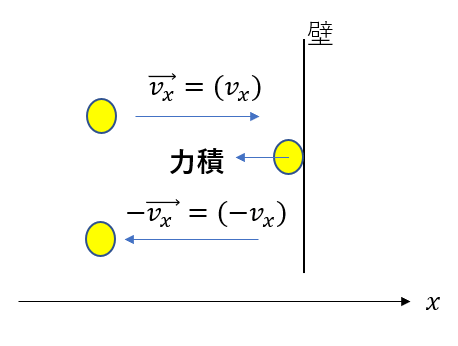
衝突の話なので、運動量を考えます。
運動量についてはこちら
運動量はベクトルで扱うんでしたね。
ベクトルについてはこちら。
衝突が弾性衝突(\(e = 1\))であるとすると
衝突後の速度は大きさが同じで向きが逆になります。
あとはあれですね。運動量と力積の関係ですね！！
AI
（はじめの運動量）＋（された力積）＝（あとの運動量）
ということで
\(m\vec{v_x} + (分子がされた力積) = -m\vec{v_x}\)
∴\((分子がされた力積) = -2m\vec{v_x}\)
今は、壁を押す力を考えたいので、
壁がされた力積を考えましょう。
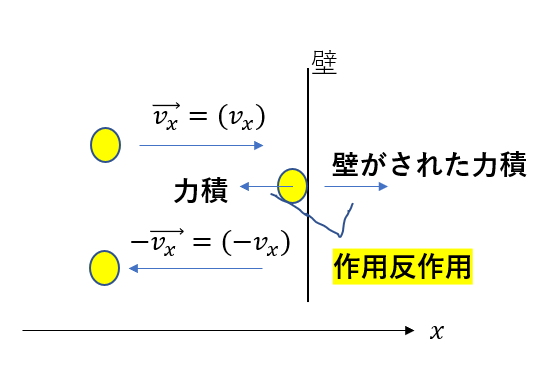
壁がされた力積は、分子がされた力積のマイナス倍です。
作用反作用からわかりますね。
ということで、一個の分子から一回の衝突で壁がされた力積は
\((壁がされた力積) = 2m\vec{v_x} = (2mv_x)\)
と表すことができます。
分子は跳ね返りますが、逆側の壁でまた跳ね返ってまた衝突して・・・
という風に何回も衝突を繰り返しますね。
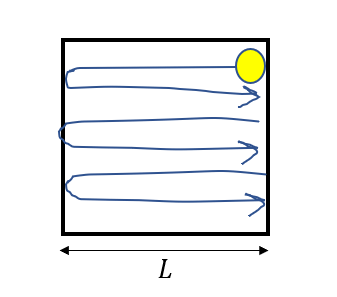
そこで、時間\(\Delta t\)の間にどれだけ衝突して、壁に力積を与えるかを考えます。
つまり
（一回の力積）×（衝突回数）を求めます。
時間\(\Delta t\)では物体は距離\(v_x t\)だけ進みますね。
（衝突前後で速さは変わらないから。）
一方分子が往復距離\(2L\)進むごとに一回衝突します。
ということで衝突回数は
\(\frac{v_x \Delta t}{2L}\)
ですね。
なので、時間\(\Delta t\)で分子一個から壁が受けた力積は
\(2mv_x・\frac{v_x \Delta t}{2L} = \frac{mv_x^2\Delta t}{L}\)
となるわけです。
ひや～、大変！
AI
頑張って（笑）。次は全分子の衝突を考えていくよ！
AKINORI
全分子が及ぼす平均の力を求める
今、1分子が及ぼした力積が
\(\frac{mv_x^2 \Delta t}{L}\)
と表されたんですよね。
だから全分子の力積を考えるときも、これを足していけばいいですよ。
\(N\)個の分子の速度の\(x\)成分をそれぞれ
\(v_{1x}, v_{2x}, … v_{Nx}\)
としてやれば、時間\(\Delta t\)で全分子が与えた力積は
\(\frac{m\Delta t}{L} (v_{1x}^2 + v_{2x}^2 + … + v_{Nx}^2)\)
です。
いや～、扱いにくいです！！
AI
そだね。だから、平均を使います。
AKINORI
速度のx成分の平均を
\(\bar{v_x^2} = \frac{1}{N} (v_{1x}^2 + v_{2x}^2 + … + v_{Nx}^2)\)
とおくと、全分子が与えた力積は次のように変形できますね。
\(\frac{m\Delta t}{L}・N\bar{v_x^2}\)
これは力積なので、全分子の平均の力を\(\bar{F}\)とすれば
\(\bar{F}\Delta t = \frac{m\Delta t}{L}・N\bar{v_x^2}\)
となるわけです。
つまり、全分子が壁に与えた平均の力は
\(\bar{F} = \frac{Nm\bar{v_x^2}}{L}\)
となります。
ここで注目したいのが\(\bar{v_x}\)です。
速さに関しては
\(v^2 = v_x^2 + v_y^2 + v_z^2\)
という関係が成り立つので、当然、平均についても
\(\bar{v^2} = \bar{v_x^2} + \bar{v_y^2} + \bar{v_z^2}\)
が成り立ちますね。
そして、分子数\(N\)は超大きい数ですよね？
そして、各分子は不規則に運動しているはずなんですよ。
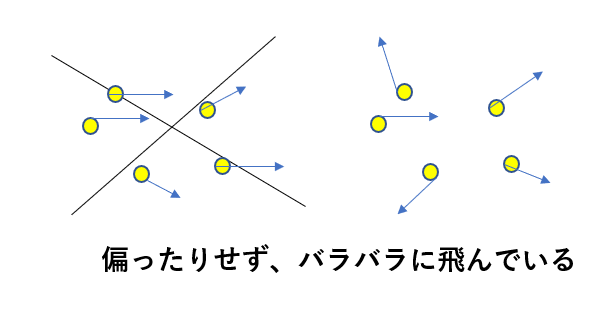
なので、各成分の平均は等しいですね。
\(\bar{v_x^2} = \bar{v_y^2} = \bar{v_z^2}\)
ということで
\(\bar{v^2} = \bar{v_x^2} + \bar{v_y^2} + \bar{v_z^2}\)
\(\bar{v_x^2} = \bar{v_y^2} = \bar{v_z^2}\)
この二式から
\(\bar{v_x^2} = \frac{\bar{v^2}}{3}\)
が成り立つわけです。
\(\bar{F}\)を書き直すと
\(\bar{F} = \frac{Nm\bar{v^2}}{3L}\)
となります。
圧力\(P\)は力を面積で割ればいいので
\(P = \frac{\bar{F}}{L^2} = \frac{Nm\bar{v^2}}{3L^3}\)
ここで\(L^3\)は立方体の体積なのでこれを\(V\)と置けば
\(PV = \frac{Nm\bar{v^2}}{3}\)
となりますね。
温度の運動エネルギーの関係をつかむ
あ！\(PV\)とくれば状態方程式を使いたくなります！！
AI
そうだね！
AKINORI
状態方程式\(PV = nRT\)を使えば
\(nRT = \frac{Nm\bar{v^2}}{3}\)
なんか\(mv^2\)が運動エネルギーっぽいですよね。
それを考慮して式変形します。
\(\frac{1}{2}m\bar{v^2} = \frac{3}{2} \frac{n}{N} RT\)
右辺に注目しましょう。
まず\(\frac{n}{N}\)は単位を見れば[mol / 個]
つまりアボガドロ定数\(N_A\)[個 / mol]の逆数\(\frac{1}{N_A}\)ですね。
そして\(\frac{R}{N_A}\)は定数です。これを\(k\)（ボルツマン定数）と置けば
\(\frac{1}{2}m\bar{v^2} = \frac{3}{2}kT\)
あれ？左辺は運動エネルギーで右辺は温度？
AI
そう。これが示したかったものです。
AKINORI
この式はつまり・・・
温度とは、分子の運動エネルギーである！！
面白い結果ですよね。
分子の運動が活発なものほど「熱い」って感じるんですね。
そして、温度の最低が-273度であるのも、ここが分子の運動が止まっちゃう点だからなんだね。
まとめ
まあ、結構細かく話したので長くなったけど、大まかに見ればそこまでステップ数は少ないです。
この話は真っ白な紙に、自分でこのストーリーを書けるように理解してください！！
- 気体分子運動論の流れ
- 分子一個の衝突
- 分子全部の衝突
- 温度と運動エネルギーの関係
