モル比熱は暗記するな！定積モル比熱と定圧モル比熱の意味と導出法
Akinoriさん。熱力学で「モル比熱」って出てくるじゃないですか？あれって何ですか？定積モル比熱とかって覚えないといけないんですか？
AI
モル比熱の意味は知っておいてほしいけど、定積モル比熱とかの値を覚える必要はないよ。今回やるように、導出できるようにしておけばOK！
AKINORI
熱力学第一法則の関連事項としてモル比熱というものが出てきます。
モル比熱というのは受験にはあまり必要のない話です。
定積モル比熱とか定圧モル比熱などありますが、
全く覚える必要がないからです。
熱力学第一法則の使い方をこちらの記事で説明をしました
ここで紹介した定圧・定積変化という過程の中で実はモル比熱というものは出てきています。
ただこちらの記事では教えていなかっただけです。
ということで、今回は
モル比熱とは？という意味の部分から説明して
モル比熱をどのように導出するかを教えていきます。
モル比熱の意味が分かる
モル比熱の導出の仕方が分かる
モル比熱がどのように使われるかが分かる
内部エネルギーとは
まず、気体の内部エネルギーについて考えます。
気体の分子運動論では
「運動エネルギー＝温度」
という関係が分かったわけですね。
↓気体の分子運動論についてはこちらを読んでね↓
その途中で
\(\frac{1}{2}m\bar{v^2} = \frac{3}{2} \frac{R}{N_A} T\)
という式が得られていました。
\(N_A\)はアボガドロ定数です。
左辺は分子一個の運動エネルギーです。
これを\(u\)とおくと
\(u = \frac{3}{2} \frac{R}{N_A} T\)
でも、気体分子はめちゃめちゃ多いわけですね。
なので、モル(mol)を使った方がいいです。
1molの気体分子のエネルギー\(U’\)は\(u\)にアボガドロ定数\(N_A\)を掛けてあげればいいですね。
（アボガドロ定数とかが分からない人は化学を勉強してください）
\(U’ = \frac{3}{2}RT\)
これは、1molの気体分子のエネルギーでした。
じゃあn[mol]だったら？
もちろん、これに\(n\)を掛けてやればいいんです。
\(U = \frac{3}{2}nRT\)
これを気体の内部エネルギーと言います。
ただ、条件があって、これは
単原子分子理想気体
の場合です！！
ん？単原子分子？なんでこういう条件が付くんですか？
AI
これは分子の形状によるからなんだ。
AKINORI
この式は\(\frac{1}{2}mv^2\)というエネルギーから導きました。
このエネルギーは\(v\)、つまり並進運動のみのエネルギーを考慮しているんですね。
例えば二原子分子だったらどうなるかというと
並進運動に加えて回転運動もあるんです。
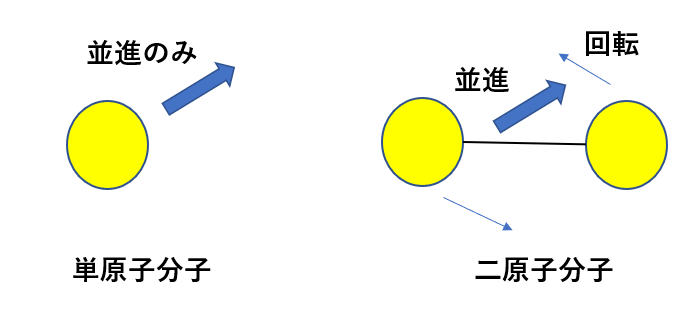
単原子分子なら、回転は無視できるんですが、二原子分子だとそうはいきません。
図のように原子がつながっている以上、これを軸に回転することができちゃうわけです。
ですから二原子分子（多原子分子）の内部エネルギーは回転の分、大きくなるんです。
二原子分子では
\(U = \frac{5}{2}nRT\)
と表されます。
モル比熱とは
じゃあ、この内部エネルギーと第一法則を使って、モル比熱っていうのを考えてみましょう！！
あの、モル比熱っていきなり出てきましたが、これって何ですか？
AI
比熱はわかるよね？それをモルにスケールアップしたものがモル比熱だよ
AKINORI
比熱の定義は
「1gの物質を温度1Kだけ上昇させるのに必要な熱量」
のことです。
\(Q = mc\Delta T\)
の\(c\)です。
ですが、今は気体を扱っていますよね。
気体をグラム基準で考えちゃうと、便利じゃないですよね。しかも、分子の種類によって質量は違うわけですから。
そこで、グラムではなくモルで比熱を考えよう！！！！
ということで、現れたのが「モル比熱」です。
つまり、
「１molの気体を1K上昇させるのに必要な熱量」
ということです。
このモル比熱を\(C\)とすれば、熱量は
\(Q = nC\Delta T\)
と書けるということです。
モル比熱は（単原子分子）の種類には関係しないけど、変化の仕方で値は変わる。つまり、定積か定圧かで変わるということ。それを第一法則を使ってみていこう！！
AKINORI
↓第一法則の応用について↓
定積モル比熱
上で紹介した記事で第一法則の応用方法をやってはいるんですが、ここでも簡単に説明します。
定積変化ということから何がわかるんでしたか？？
はい！\(\Delta V = 0\)なので\(W = 0\)ですね！！
AI
ということで第一法則
\(Q = \Delta U + W\)
から
\(Q = \Delta U\)
つまり
\(Q = \frac{3}{2}nR\Delta T\)
さて、これをよく見てみましょう。
\(n = 1, \Delta T = 1\)として見ると
\(Q = \frac{3}{2}R\)
ですよね。
もしかして、これってモル比熱ですか？
AI
そう！\(n = 1, \Delta T = 1\)ということは「１molの気体を1K上昇させる」ってこと。その熱量が\(Q = \frac{3}{2}R\)って言ってるんだね！
AKINORI
これが「定積モル比熱」です。
\(C_V = \frac{3}{2}R\)
とすれば
\(Q = nC_V\Delta T\)
となっていることがわかりますね。
また
\(\Delta U = nC_V \Delta T\)
と表せます。
これは単原子分子に限らず、多原子分子でも成り立ちます。
もちろん、\(C_V\)の値は変わりますがね。
定圧モル比熱
定圧変化では何がわかるんでしたっけ？？
はいはい！！仕事が\(W = P\Delta V\)と書けます！！
AI
仕事は圧力一定のときに
\(W = P\Delta V\)
と表せるんでしたね。
これを使って第一法則を書き換えると
\(Q = \frac{3}{2}nR\Delta T + P\Delta T\)
さらにさらに、状態方程式から変化量の関係をつくると
\(P\Delta V = nR\Delta T\)
です。
\(P, n , R\)は変化し得ないので、左辺と右辺の変化量を考えるときは、\(V, T\)のみを考えればいいんですね。
まとめると
\(Q = \frac{5}{2}nRT\)
さっきと同じですね。\(n = 1, \Delta T = 1\)としたってことは、「１molの気体を１K上昇させる」ってことだから\(\frac{5}{2}R\)は比熱ってことですよね。
AI
その通り！！よくわかってるね～
AKINORI
これを「定圧モル比熱」って言います。
\(C_p = \frac{5}{2}R\)
こうおくと
\(Q = nC_p \Delta V\)
となります。
定圧モル比熱の方が大きいわけは？？
最後にこれを考えてみましょう
AKINORI
さっき求めた、定積モル比熱と定圧モル比熱。
値が定圧モル比熱の方が大きいですよね？
この理由は、何でしょう？
え～と。定圧だと、温度上昇以外に、仕事するのに熱量を使っちゃうからかな～？
AI
正解！！
AKINORI
定積では
\(Q = \Delta U\)
という風に、もらった熱量がすべてエネルギー上昇、つまり温度上昇に用いられてますね。
一方で定圧では
\(Q = \Delta U + W\)
という風に、もらった熱量の一部を仕事に使っちゃうわけです。
ですから、同じ温度だけ上げるには、定圧の方が熱が必要なので、モル比熱も大きいんですね。
こうやって、式から状況を判断するのは面白いですね！！
AI
入試でも状況を整理することが点を取るカギになるからね。結構重要だよ。
AKINORI
とまあ、モル比熱について説明したけど、これは覚えなくていいからね。モル比熱は第一法則を応用したら自然と出てくるものだからいつでも導けるようにしよう！！
AKINORI
二原子分子の場合
最後に、二原子分子の場合は内部エネルギーが違うのでモル比熱も当然変わります。
\(U = \frac{5}{2}nRT\)ということが分かっていれば
\(C_V = \frac{5}{2}R\)
\(C_p =\frac{7}{2}R\)
と導けますね。
（ちなみにどんな分子でも「\(C_V + R = C_P\)（マイヤーの関係式）」が成り立ちます）
以上です！！それでは！！
Comment
定圧モル比熱の説明のところなんですが、
=3/2Δ+Δ → =3/2Δ+Δ
=5/2 → =52Δ
ではないでしょうか？？？
とてもわかりやすかったので、連絡しました。