【物理】熱サイクルの問題はこれしかない!熱効率と・・・

熱効率の意味が分かる
熱サイクルの問題と関連して理解できる
熱サイクルの問題が解ける
どうも!受験物理setupのあっきーです。
私、熱力学でよく出てくる熱サイクルがいまいちわからないんです。グラフの読み取りとかが難しくて・・・
 AI
AI
このような悩みはありませんか?
実は、熱サイクルの問題は問われることが決まっていて、熱効率の意味さえ知っていればほぼすべての問題が解けます。
なぜなら、熱サイクルであろうと熱力学の問題はどんな問題でも、「一定」を探して状態方程式や第一法則を使えば良いだけだからです。
この記事では、熱サイクルの問題で問われるところを伝えながら、熱効率の意味を教えていきます。
この記事を読み終えると、熱サイクルの問題が楽勝になり、どんな熱サイクルの問題も解くことができます。
目次
熱サイクルとは?

そもそも熱サイクルとは何かを確認しましょう。
熱サイクルというのは気体を何段階か変化させて元の状態に戻して1週させることを言います。
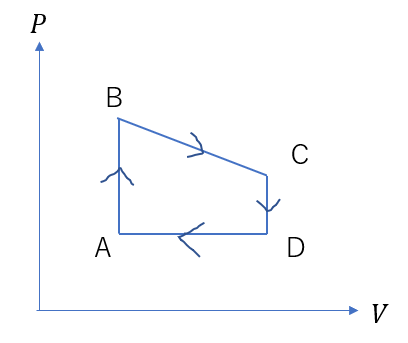
このようにグラフの形で表されて一周していますね。
グラフの取り方は
P-V, T-V, P-T
の3種類ありますが、P-Tはほとんど見たことがありません。
ただ熱サイクルとカッコよく言っていますが、気体の状態変化と何も変わらないわけです。
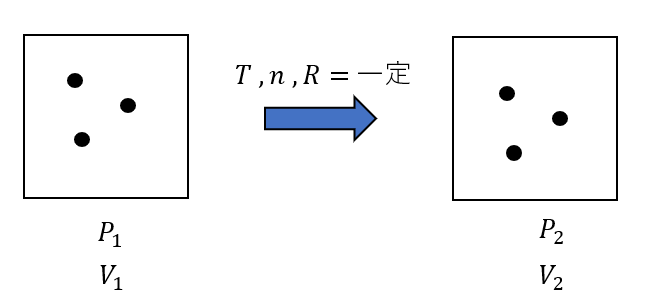
気体の変化を追うときは、今までこうやって図を書いてきましたよね。
これをグラフに書き換えただけです。
なので熱サイクルの問題は、もはやグラフという図を与えられている超ラッキー問題なのです。
そして問われることは決まっています。それが次の3つです。
・熱効率
・グラフの書き換え
・温度、圧力、体積の最大値
今回はこれを問題形式で実際に確認してみましょう。
熱サイクルの問題
1molの単原子分子からなる理想気体を、ピストンのついたシリンダー内に封じ込め、外部と熱や仕事のやり取りをすることで、図のようにサイクルA→B→C→A緩やかに変化させる。状態Cの絶対温度を\(T_1\)、気体定数を\(R\)として次の問いに答えよ。
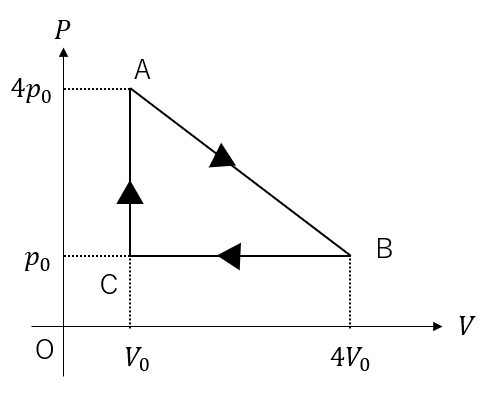
(1)このサイクルの熱効率を求めよ。ただしA→Bで得た熱量を\(Q_{AB}\)としてよい。
(2)AB間における絶対温度の最大値を\(T_1\)を用いて表せ。またその時の体積を\(V_0\)を用いて表せ
(3)このサイクルの変化を、横軸を体積、縦軸を絶対温度にとってグラフに表せ
熱サイクルの問題が来たらまずやってほしいこと

熱サイクルの問題が来たら小問に進む前に必ずやってほしいことがあります。
グラフで書かれていない情報を書き足してください。
今回の場合、圧力と体積の情報がありますよね。でも、温度の情報がグラフに書かれていませんね。
これを求めて、書き足していきます。
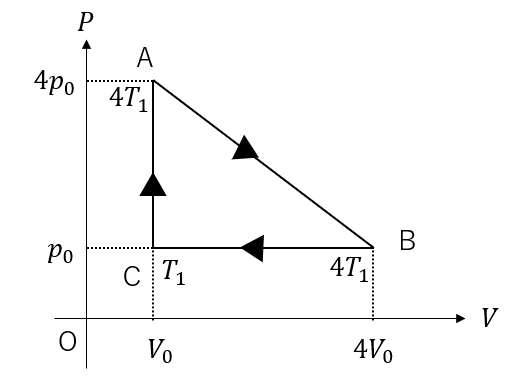
Cの温度が\(T_1\)とされているので、\(T_1\)を使って表していきます。
C→Aについて
C→Aでは「体積一定」の変化が起こってますね。ここから状態方程式を使うと

このようになりますね。(状態方程式についてはこちら)
これをC→Aの過程で使えばこうなります。
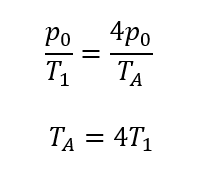
B→Cについて
B→Cでは圧力一定となってますね。状態方程式を使えば
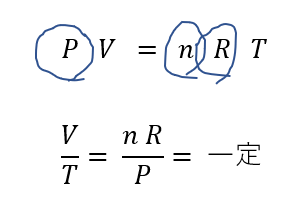
となりますね。
先ほどと同じようにやると

このように求められますね。
このように、グラフで直接与えられていない情報はあらかじめ求めておいてください
熱効率とは:「熱をどれだけ仕事に変えたか」
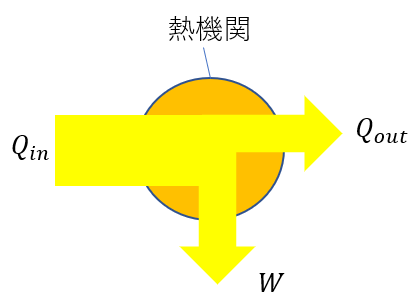
(1)は熱効率という新しい言葉が出てきたので、まずはこれを説明します。
サイクルを巡回させることで、気体は仕事をします。また、このサイクルは熱をもらうことで状態が変化していきます。
熱効率というのは気体がした仕事\(W\)、気体が得た熱量を\(Q_{in}\)とすると次のように表せます。
熱効率
\(e = \frac{W}{Q_{in}}\)
つまり、熱効率は「もらった熱をどれだけ仕事に変えられたか」というのを表します。
自動車などのエンジンはなるべくこれを高くしたいんですね。
熱効率は\(0 < e < 1\)の値を取ります。
\(e\)が1に近づくほど、熱を仕事にうまく変えられていて効率が良いということです。
\(e = 1\)ならもらった熱をすべて仕事に変えるんですよね?では、もし\(e = 1\)ではなかったらどうなるんですか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
仕事に使われずそのまま外部に逃げてしまうんだ。
 あっきー
あっきー
この1サイクルでは、熱をもらっても一部はそのまま外に逃げてしまいます。

つまり、
\(W = Q_{in} – Q_{out}\)
とも表すことができます。そしてこれを使って式変形ができます。
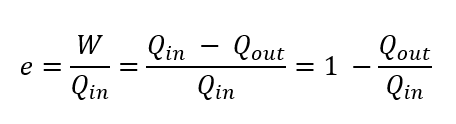
覚える必要はありませんが、式変形にできるようにしてください。
なお、\(e = 1\)、つまり熱をすべて仕事に変えられるような熱機関は存在しないようです。
さて、これを見ると熱効率で必要なものは次の二つの情報です。
気体がした仕事の和
気体がもらった熱量の和
この2つの情報をグラフから読み取っていきます。
気体のした仕事の総和

まずは気体のした仕事\(W\)を求めます。
気体が仕事をするには、体積が変化していないといけません。
つまりこのサイクルではA→B, B→Cの過程で仕事をしています。
よし後は\(W = P \Delta V\)を使って・・・
 リケジョになりたいAIさん
リケジョになりたいAIさん
ちょっとまって!それ本当に使える?
 あっきー
あっきー
気体のした仕事は\(W = P\Delta V\)
・・・としたい気持ちは分かりますが、これは\(P = 一定\)という条件でのみ使えます。
ですがA→Bの過程はどうみても\(P = 一定\)ではないですよね?
なので使えないのです。
となれば、できることは一つ。
グラフの面積を求める!!
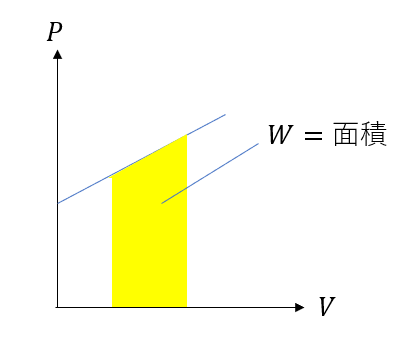
A→Bの過程でした仕事と
B→Cの過程でした仕事はそれぞれ図の面積になります。
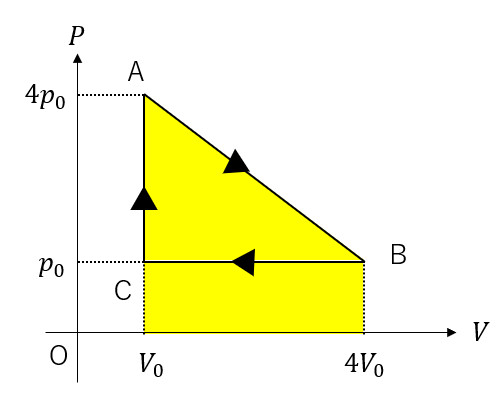
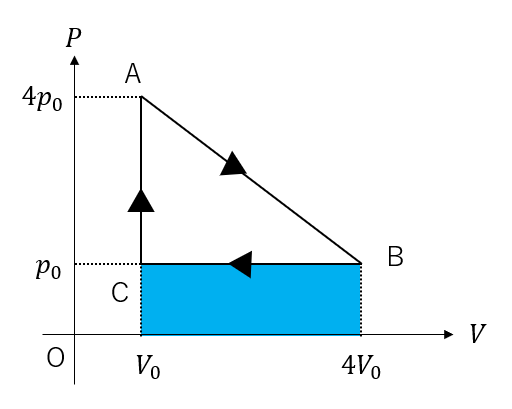
このうち、B→Cはされた仕事になり、この部分は相殺されます。
つまり、求めたい仕事は次の図の面積になります。
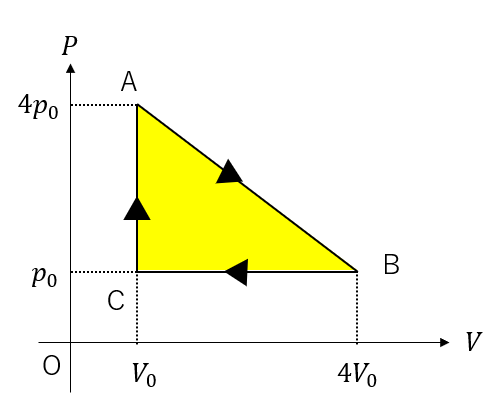
三角形の面積なので簡単に求められますね。
\(W = \frac{9}{2}p_0V_0\)
となります。
もらった熱量を求める

仕事が求まったので、次はもらった熱量を求めます。
ここでは、放出したものは含めません。仕事ではされた仕事も含めるのでこの辺りを間違えないようにしましょう。
熱量を求めるには第一法則以外ありませんね。(第一法則についてはこちら)
\(Q = \Delta U + W\)
について、熱量をもらうには右辺が正になっていないといけません。
つまり、温度や体積が増加する過程です。
この熱サイクルではC→A, A→Bで熱量を得ます。
C→Aで得た熱量
この変化では体積一定なので\(W = 0\)です。
また単原子分子なので\(\Delta U = \frac{3}{2}nR\Delta T\)と表せます。
ということで得た熱量\(Q_{AB}\)は次のようになります。

A→Bは\(Q_{BC}\)と表してよいと問題文に書いてあります。(これは高校生の範囲では求めらません)
あとは熱効率を求めるだけです。
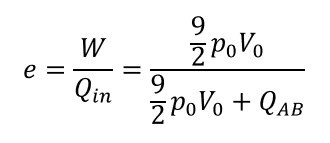
となります。
数学で最大値と言えば二次関数

(2)はちょっと手強いです。手強いというより、公式を当てはめていけば解けてしまう物理の問題には珍しいタイプだからです。
数学でこの手の問題が出たら多くの人は答えられると思います。
数学で「最大値」ときたら、グラフを書きますよね?やっぱり二次関数ですよね?
物理でもこれをやっていきます。
(2)の問題では、「\(T\)の最大値を求め、その時の\(V\)も求めよ」と書いてあるので、
\(T = (Vの式)\)にして、最大値を求めればOKですね。もちろん使えるのは状態方程式です。
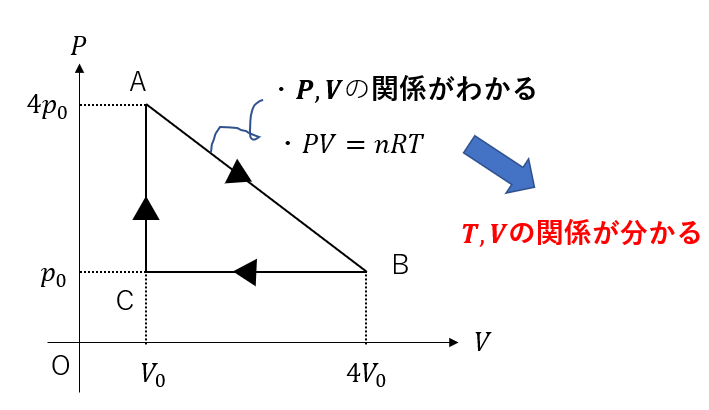
グラフから\(P = (Vの式)\)の形で表し、状態方程式を使って\(P\)を消去すれば
\(T = (Vの式)\)と表すことができるわけです。
グラフは直線のグラフになっているので、簡単に関係式を導くことができます。
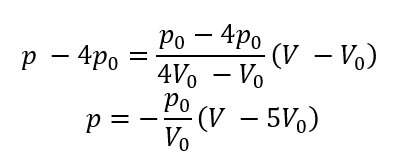
これを状態方程式に代入してみます。
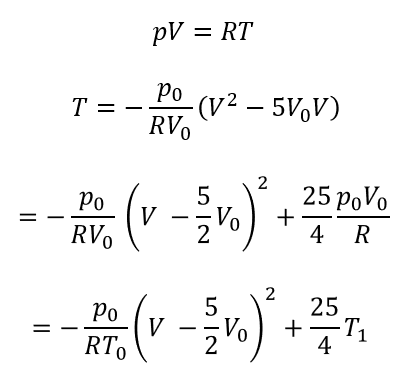
\(T = \)の形にしてみたら、\(V\)の二次関数になったので、みなさん大好きな平方完成をして最大値を求めていきます。
つまり
\(V = \frac{5}{2}V_0\)で最大値\(\frac{25}{4}T_1\)をとる
これが答えです。
グラフと状態方程式を使って書き換える

(3)はグラフの書き換え問題です。
問題で与えられているグラフと状態方程式を使って書き換えられるかがポイントです。
と言っても(2)でやったことをすべての過程で行えばいいだけです。
A→Bは(2)で導きました。
B→Cでは圧力一定ですね
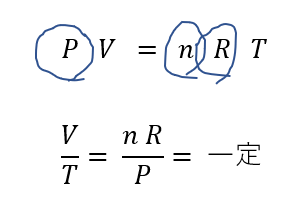
つまり\(T = kV\)となり、直線のグラフになります。
C→Aでは体積一定の変化なので、T-Vグラフに置き換えても体積一定になるように書けばOKです。
A,B,Cそれぞれの状態での温度は最初に求めていますので、あとはグラフを書くだけです。
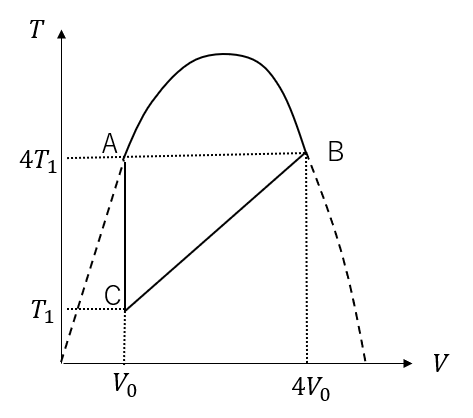
このように書くことができます。
まとめ:熱サイクルで問われることは3つ

いかがでしたか?
熱サイクルで問われることは3つしかありません。
ちなみにこの問題はかなり難しいです。
本来なら誘導はしっかりついていますので安心してください。
とはいえ、誘導に頼らずに解けることが大事です。今回の熱サイクルの復習や類題を解くなどをして自分のものにしましょう。
熱サイクルの問題で問われること
・熱効率
・グラフの書き換え
・最大値
熱効率について
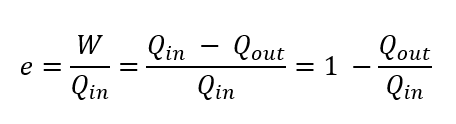

グラフ書き換えと最大値について
→元のグラフと状態方程式を使って二次関数にもっていく