熱力学で要注意！グラフから仕事を求める問題
熱力学ではグラフを使った問題がよく出てきます。今回はグラフを使って仕事を求める場合を考えてみましょう。
AKINORI
特に問われやすいのが
自分でグラフを書いて仕事を求める
これです。
状態方程式を使って\(P,V\)の関係を考えてグラフにする。
そういう問題も少なくないです。
自分でグラフを考えるのか・・・難しそうだけど頑張ろう！
AI
問題
単原子分子理想気体をシリンダー内に入れる。気体はヒーターによって加熱することができる。また、シリンダー内には面積\(S\)のピストンがばね定数\(k\)のばねに取り付けられており、ピストンの右側では大気が出入りすることができる。はじめ、気体の圧力、体積、温度がそれぞれ\(P_0, V_0, T_0\)であり、ピストンは静止しており、ばねは自然長であった。この状態をAとする。なお、大気圧は一定である。
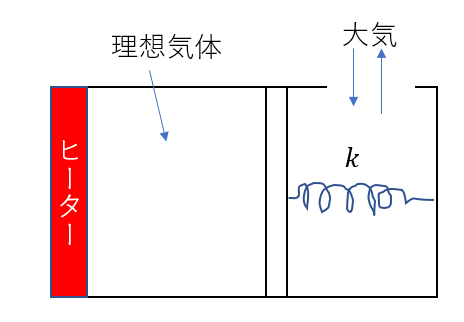
気体を加熱することで体積を\( V_1\)になったところでピストンは静止した。この状態をBとする。
（１）状態Bでの体積\(P_1\)を求めよ
（２）A→Bの変化で気体がした仕事を求めよ。ただし、\(P_1\)を用いて表してよい。
（１）ピストンのつり合いを考えればOK
状態Bではピストンが静止しているからつり合いを考えれば良さそうですね
AI
まず、大気圧を考えておきましょう。
はじめの状態でばねは自然長だったので、ピストンが静止しているには当然
理想気体と大気の圧力が等しくないといけませんね。
つまり、大気圧は\(P_0\)です。
大気圧は\(P_0\)で一定の値をとっていきます。
では、状態Bを考えていきましょう。
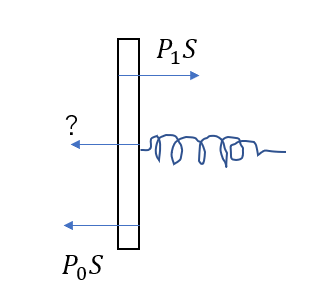
ここで、問題なのがばねの弾性力です。
弾性力を考えるには伸び（縮み）が必要ですよね。
今回体積が\(V_0\)から\(V_1\)に移動したので、
\(k(V_1 – V_0)\)
としてはいけません。
これは「体積」です。「長さ」が必要なんです。
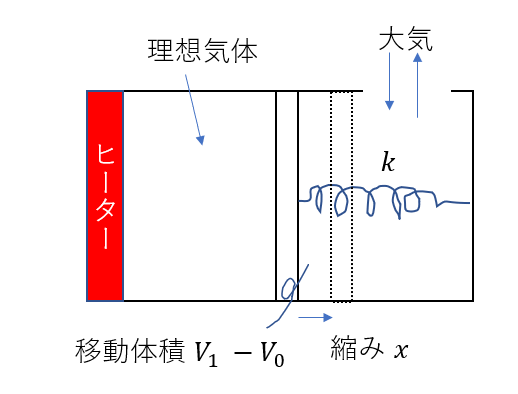
図を見てもわかるように、
縮みを\(x\)とすれば、
断面積が\(S\)ですから
\(S・x = V_1 – V_0\)
ですね。（底面積×高さ＝体積）です。
つまり、
\(x = \frac{V_1 – V_0}{S}\)
これで、ばねの弾性力がわかりますね。
あとは力のつり合いを立てるだけです。
右向きを正にして
\(P_1S – P_0S – k\frac{V_1 – V_0}{S} = 0\)
∴\(P_1 = P_0 + k\frac{V_1 – V_2}{S^2}\)
これが答えです。
（２）P,Vの関係を求めてグラフにする
仕事を求めるから\(P\Delta V\)にしたいけど、圧力って変化するよね・・・
AI
そんな時は、グラフを書いて面積を求めればOK！
AKINORI
問題はグラフが書けるかどうかですね。
今状態Bに関して式を立てました。
が、A→Bの間では（１）で求めたような関係が成り立ちます。
A→Bの間のどっか適当な状態Cをとってきてその圧力、体積を\(P, V\)とすると、やっぱり
\(P = P_0 + k\frac{V – V_0}{S^2}\)
という関係が成り立ちます。
さて、この式を見てください。
分かりやすいようにもう少し変形します。
\(P = \frac{k}{S^2}V + P_0 – \frac{kV_0}{S^2}\)
このうち\(P,V\)のみが変化する値です。
・・・あれ？\(y = ax + b\)の形になってません？
AI
そう。P-Vグラフは直線になるってことです！！
AKINORI
なので、簡単にグラフが書けますね。
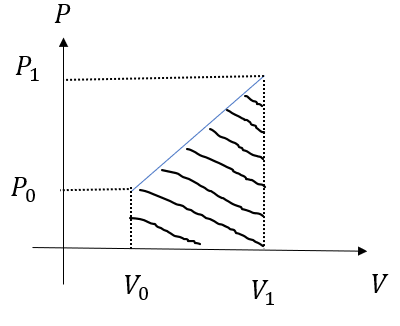
このような直線のグラフになります。
あとは、図の面積（台形）を求めればいいので
\(W = \frac{(P_1 + P_0)(V_1 – V_0)}{2}\)
これが答えです。
なるほど！こうやってグラフを自分で書いて仕事を求めることもあるんですね。
AI
そう！仕事に限らず、いろんな場面でグラフを使って求めることもあるし、グラフそのものを書かせる問題も多いから慣れておこう！
AKINORI
ちなみに・・・
ちなみに、さっきの仕事をこうやって解釈することができます。
こう見ると「圧力×体積」と表せていることがわかります。
実は、グラフでも、同じ面積の長方形に書き換えることがわかっています。
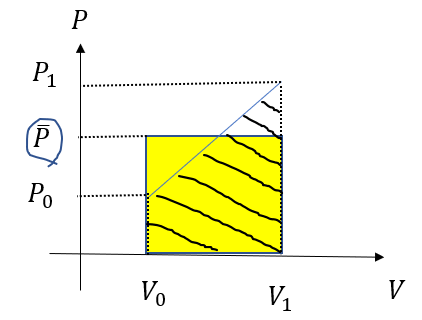
このように、絶対に面積が同じ長方形を書くことができます。
グラフが曲線になっても同じです。
（数Ⅲをやっている人なら証明できるので、調べてみては？）
そして、この長方形にした時の、縦（横）の長さがまさに平均になるのです！！
知っておくとどこかで使えるかもしれません。
それでは！
