【物理】気体の状態方程式の意味と使い方。ボイルの法則？そんなのいらないよ
・状態方程式の意味と使い方が分かる
・ボイルの法則などを覚える必要がなくなる
・熱力学の問題が楽々解けるようになる
どうも！受験物理Set UpのAkinoriです。
ボイルの法則とかシャルルの法則とか。あれ覚えるのしんどいです。
AI
君は忠実なんだね（笑）。確かに、教科書とか学校の授業でこういう法則を紹介しているよね。でも、ぶっちゃけ、いらないです！覚える公式は「状態方程式」これだけです。
AKINORI
熱力学で出てくるこんな法則聞いたことありますか？
- ボイルの法則
- シャルルの法則
- ボイル・シャルルの法則
あると思います。化学にも出てきますしね。
ですが、皆さんに残念なお知らせがあります。
これらは覚える必要がありません！！
あなたが覚えるべき公式は気体の状態方程式と呼ばれるものです。状態方程式は熱力学で最も重要な公式であり、使いこなせなければ詰みます。
しかし、これさえ知っていれば、熱力学の50%は理解したも同然です。
状態方程式が分かっていればボイルの法則、シャルルの法則などを覚える必要は一切ありませんし、問題だって楽々解くことができます。
ということで、今回は状態方程式の意味とその使い方を問題を見せながら解説していきます。
理想気体の状態方程式とは？
まずは、その状態方程式というのを先に出しておきます。
これは導出とか無いので覚えてください。
- 理想気体の状態方程式
\(PV = nRT\)
これが状態方程式です。正確には「理想気体の」が付きます。
理想気体というのは
「分子の大きさと分子同士の相互作用（分子間力）を無視した理想的な気体」
という定義です。
現実にある気体（実在気体）は小さいながらも、分子には大きさがありますし、それぞれ力を及ぼしあっています。
これを扱うのは厄介なので、原則は理想気体を扱っていきます。
（理想気体や実在気体の細かい話は化学に任せます）
この\(PV = nRT\)ですが、それぞれの文字の意味は
- \(P\)：圧力[Pa]
- \(V\)：体積[m3]
- \(n\)：物質量[mol]
- \(R\)：気体定数（8.31）[J / (mol・K)]
- \(T\)：絶対温度[K]
です。特に\(T\)は絶対温度です。
ケルビンです。
なので、問題で[℃]が与えられたら[K]に変えないといけません。
これは度[℃]に273を足せばOKです。
例えば２７℃だったら
\(27 + 273 = 300\) [K]
です。
状態方程式の使い方
ではでは、状態方程式の使い方です。
これ、めちゃめちゃ重要です。今後熱力学の問題を解くにしても、そして入試問題を解くにしても絶対に使うやり方です。
まず、そのやり方を言いますよ！
- 図を書く
- 「一定」を探す
- 状態方程式で「左辺＝一定」の形にして適用
３つほど簡単な例題を出してやってみます
例１
体積を変えることができる密閉容器がある。はじめ体積が0.10m3、温度が27℃であった理想気体を、温度が127度になるまで加熱したとき、気体の体積を求めよ。なお、この操作では圧力は変化しないとする。
さっき示したやり方通り解いていきましょう。
まずは、図を書くんですね。
AI
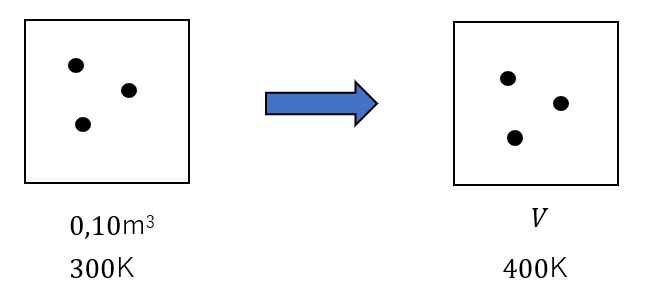
この例は図を書くまでもないって思うかもしれないけど、絶対に書いてください。また、図のように分子の個数も簡単に表しておいてください。この分子の個数が\(n\)[mol]を表します。
そして、「一定」を見つけるんですね。
AI
今回一定なのは、\(P, n ,R\)です。
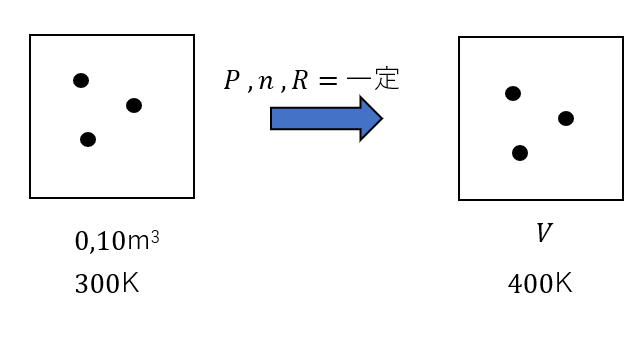
このように、さっき書いた図に書き足しておきます。
そして、状態方程式を「左辺＝一定」にする。
AI
そして、状態方程式を次のように整理します。
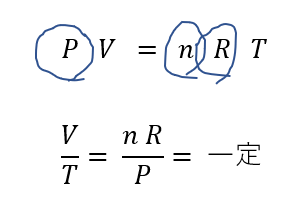
一定のものに丸をしてあります。
これを右辺にまとめるように式変形します。
すると、\(\frac{nR}{P}\)は一定になりすよね。
この\(\frac{V}{T} = 一定\)を使えばOKです。
\(\frac{0,10}{300} = \frac{V}{400}\)
∴\(V= o.13\)[m3]
となるわけです。
うわ。すごい簡単ですね。
AI
そう。これができれば問題ないです。
AKINORI
あれ？途中で出てきた\(\frac{V}{T} = 一定\)って「シャルルの法則」ですよね！？
AI
そう。状態方程式から「シャルルの法則」を導けるから別に覚えなくていいんだ。
AKINORI
シャルルの法則はまさにそうで
圧力が一定の時、一定量の気体の体積\(V\)は、絶対温度\(T\)に比例する。
\(\frac{V}{T} = 一定\)
（セミナー物理基礎＋物理）
と説明されています。
でも、圧力一定とか条件あるし、よくわかりませんね。
でも、今やったように状態方程式を使った途中経過でしかないので、覚える必要なんかないんです。
＊状態方程式はボイルの法則やシャルルの法則から導かれた一般形なので、状態方程式からボイルの法則などが導けるのは当たり前です！！
例２
体積を変化できる密閉容器がある。はじめ圧力、体積がそれぞれ\(P_1, V_1\)である理想気体を、温度一定で体積を\(V_2\)に変化させた。変化後の圧力\(P_2\)を求めよ。
もちろん、やるべきことは同じです。
まずは図ですね。
AI
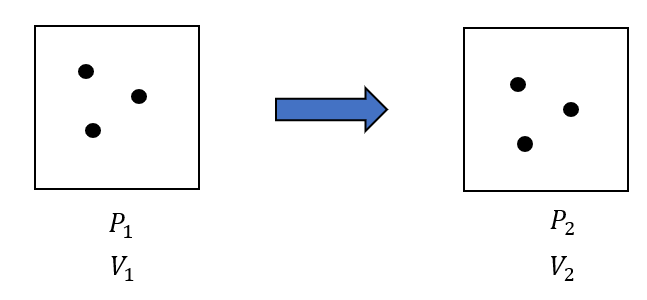
このうち\(P_2\)が求めたいものですね。
次は「一定」を探すんでしたね。
AI
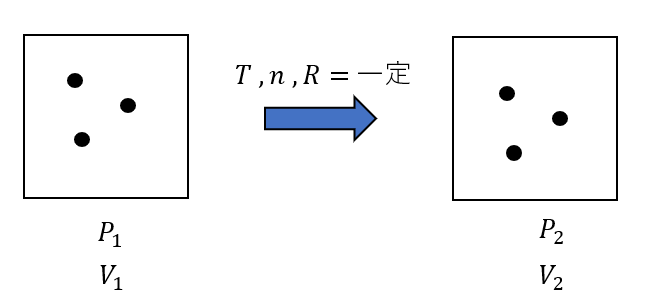
最後は「左辺＝一定」と式変形するんでしたね。
AI
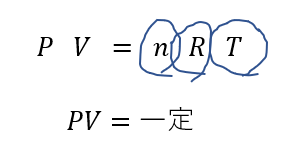
あとは変化前後で等号を結ぶだけです。
\(P_1V_1 = P_2 V_2\)
∴\(P_2 = \frac{V_1}{V_2}P_1\)
これが答えです。
そして、\(PV = 一定\)というのは「ボイルの法則」そのものです。
やっぱり状態方程式から導けますね。状態方程式の条件を絞るとこういう法則が出てくるわけです。
という風に、状態方程式一つでいろんな問題が解けちゃうわけです。
ボイルの法則やシャルルの法則なんて覚える必要なし。
さらには、状態方程式を使えば
\(\frac{P}{T} = 一定\)
のような、名前の無い法則？
も出せるわけです。
うわ～～。すごい簡単じゃないですか！！もっと早く教えてくれたらいちいち面倒な法則を覚えずに済んだのに・・・
AI
まあまあ（笑）。これから熱力学を学ぶ人や、法則を一個一個覚えていた人、今日からこのやり方で問題を解いていきましょう。これは化学の気体分野でも使える方法だからマスターしておいてね。
AKINORI
まとめ
- 理想気体の状態方程式
\(PV = nRT\)
- 状態方程式の使い方
- 図を書く
- 「一定」を探す
- 状態方程式を「左辺＝一定」の形にして適用
↓状態方程式の問題演習はこちら↓
