知らなきゃ損!短期間で力を伸ばす高校物理の意外な勉強法

こんにちは!受験物理Set Upです。
無料テキスト利用者もおかげさまで増えてきて、また講座に参加いただける方も大変増えております。僕はうれしいです。
講座に入った方々には質問やコンサルも行っているのですが、100%こんな質問が来ます。
物理の勉強法でオススメなものありますか?
 AI
AI
はい。ダントツで多い質問です。
誰でもオススメの勉強法はやっぱり知りたいですよね。
物理に限った話じゃないですが、勉強法を間違えるとライバルと圧倒的な差がついてしまいます。
「うわ、こんなに問題集やっても模試の点数上がらないよ・・・」
と、ずっと成績が伸びない自分に不安を感じることもあります。(まさに僕みたいに)
そして受験に不合格・・・
なんてことになりたくないですよね?
そこで、今回は
短期間で受験を勝つ力を身に付ける意外な勉強法を
高校生で勉強を頑張っているであろうあなたに特別に教えたいと思います。
目次
高校生の99%が知らない勉強法

これは誰も知らない勉強法です。
高3の秋までセンター模試40点の僕を救った先生から教わった本当にすごい勉強法です。
これは日々の問題演習ではもちろん、実際の試験でも使える超優れものなんです!!
その勉強法がこれです。
分かること先に求めちゃえ勉強法
です。
(この勉強法の名前募集してます!)
・・・?なんかダサいです(笑)
 AI
AI
まあ、そんなこと言わずに。内容は画期的ですから
 AKINORI
AKINORI
問題を解く時にやりがちなこと

問題を解く時にどうやって解いていますか?
え?普通に(1)を解いて(2)を解いて・・・
 AI
AI
普通はそうだよね。
 AKINORI
AKINORI
問題集の問題、あるいは模試、過去問の問題はどれも問題の設定があって(1)、(2)・・・
という感じで各問がつづいていきますよね。
例えばこんな感じで
シリンダー内に1モルの単原子分子理想気体が入っている。図はこの気体の1サイクルの状態変化を表すもので、横軸は絶対温度\(T\)、縦軸は体積\(V\)である。状態Aにおける温度と体積は, \(T_0, V_0\)であり、気体定数は\(R\)とする
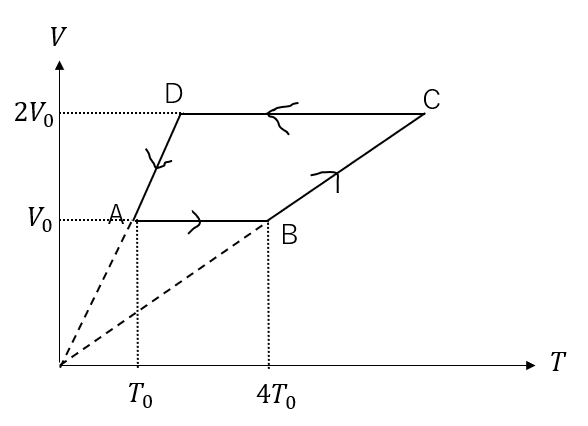
(1) 状態Aにおける圧力を求めよ。また、状態CとDにおける圧力と温度をそれぞれ求めよ。
(2) この状態変化を、縦軸に圧力、横軸に体積をとったグラフに表せ。
(3) 1サイクルの間に、気体が真に吸収した熱量の総和\(Q_{in}\)(放出した分は含めない)を求めよ。
(4) 1サイクルにおける(熱)効率を求めよ。
(河合出版 名門の森 問題51)
この問題を見たときに誰もがこのように解きますよね。
(1)は状態方程式で解こう・・・よし解けた。(2)は(1)の流れから・・・よし解けた。(3)は第一法則かな・・・
 AI
AI
問題設定を読んで
(1)を読んで、解いて。
(2)を読んで、解いて
・・・
いたって普通ですよね。
ですが、そうではないんです!!
これはただ問題を解いているだけです。
ではどうやって解くか実際にお見せしますね。
最初の設定からわかることをすべて書きだす

問題設定がありますよね。そこはもちろん読むんですが、その先の小問は読みません!
え?読まないんですか?それじゃ問題解けないじゃないですか!
 AI
AI
まあまあ、焦らないで(笑)もちろん解きますよ。
 AKINORI
AKINORI
小問を読んでから解くのではなく、小問を解く前にある程度答えを導いてしまうんです。
問題設定を読んだ段階で自分ができる範囲で導ける式や数値を出しておくのです。
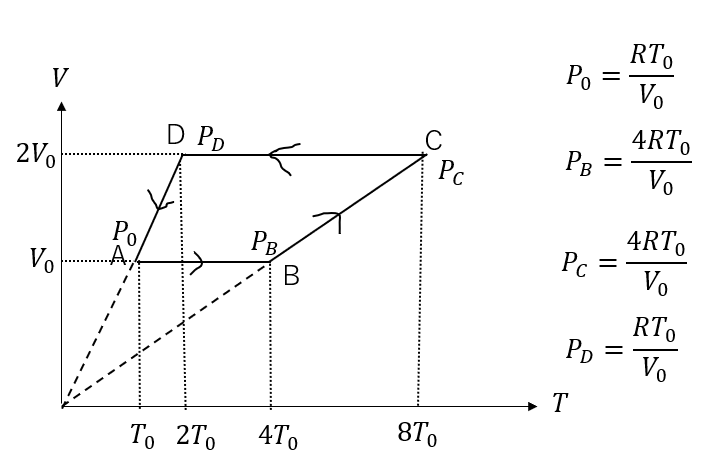
各状態の圧力・体積・温度が求められる
今回の例題では、まずはこう考えてください。
熱力学の問題だから状態方程式と第一法則は絶対に使うね。
 AKINORI
AKINORI
なので、この二つを使ってできる限りのことをすればいいんですよね。
問題設定を読んだ段階で各状態の圧力・体積・温度などはすべて求められます
Aについて
\(PV = nRT\)をそのまま使って
\(P_0 = \frac{RT_0}{V_0}\)
Bについて
\(P_B = \frac{4RT_0}{V_0}\)
となりますね。
Cについて
また、BCに関してはグラフが1次関数のですよね。つまり
\(V = kT\)(\(k\)は定数)
となるような形になるのです。
\(PV = nRT\)を変形して
\(V = \frac{nR}{P}T\)
とすれば\(\frac{nR}{P} = k\)となればいいわけですよね。
つまりこのB→Cの変化では\(P = 一定\)となります(D→Aも同様)。
ですから\(P_C = P_B = \frac{4RT_0}{V_0})
となりますし、\(\frac{V}{T} = 一定\)なので
\(\frac{V_0}{4T_0} = \frac{2V_0}{T_C}\)
\(T_C = 8T_0\)
と表せるわけです。
Dについて
D→Aも\(P = 一定\)なので
\(P_D = P_0 = \frac{RT_0}{V_0}\)
となり、
\(\frac{V}{T} = 一定\)なので
\(\frac{V_0}{T_0} = \frac{2V_0}{T_D}\)
\(T_D = 2T_0\)
と表すことができます。
グラフ問題だから熱効率とか求められるだろうな・・・
状態方程式はたっぷり使ったので残るは第一法則です。
こういう熱サイクルの問題はほぼ間違いなく熱効率の問題が出てくると考えていいでしょう。
なので、熱効率を求めます。
熱効率は
\(e = \frac{W}{Q_{in}} = \frac{Q_{in} – Q_{out}}{Q_{in}}\)
なので、吸収熱量\(Q_{in}\)と気体のした仕事\(W\)を求めればいいんです(もしくは放出した熱量\(Q_{out}\))。
第一法則
\(Q = \Delta U + W\)
の左辺がもらった熱量です。また右辺の内部エネルギーの変化は温度変化を表します。
もし右辺がマイナスになれば左辺は放出した熱量になってしまうので本来求めたい\(Q_{in}\)が求められません。
つまり右辺がプラスになるような過程だけを考えればいいのです。
温度や体積が大きくなるサイクルです。それはA→BとB→Cですね。
ここで第一法則を適用すればいいのです。
吸収熱量を求める
A→Bについて
ここは体積変化がないので\(W = 0\)ですね。
また\(\Delta U = \frac{3}{2}R\Delta T = \frac{9}{2}RT_0\)
ということで第一法則を使うと
\(Q_{AB} = \frac{9}{2}RT_0\)
となります。
B→Cについて
ここは先ほど見たように圧力が一定です。つまり
\(W = P\Delta V\)と表せます。これは状態方程式を使って
\(W = R\Delta T\)とも表すことができます。
後は第一法則を使うと
\(Q_{BC} = \frac{3}{2}R\Delta T + R\Delta T = \frac{5}{2}R\Delta T = 10RT_0\)
となります。
つまり吸収した熱量は
\(Q_{in} = Q_{AB} + Q_{BC} = \frac{29}{2}RT_0\)
となります。
仕事を求める。
次は仕事を求めます。これはした仕事をプラス、された仕事をマイナスとして考え、すべて足し合わせた全体の仕事を求めていきます。
仕事は体積変化がないところでは0なので、B→CとD→Aだけ考えればOKです。
しかもこのふたつの過程はいずれも圧力が一定なので
\(W = P\Delta V = R\Delta T\)
と表すことができます。
B→Cについて
\(W_{BC} = 4RT_0\)
D→Aについて
\(W_{DA} = -RT_0\)
ということで全仕事は
\(W = W_{BC} + W_{DA} = 3RT_0\)
となります。
最後に熱効率を求めよう
必要な情報はすべて求めたので後は計算するだけです。熱効率は
\(e = \frac{W}{Q_{in}} = \frac{6}{29}\)
と導くことができました。
なるほど。最初の問題文だけでもここまで求めることができるんだ!
 AI
AI
小問を見ないことで誘導に頼らずに自分の知識だけで答えることができるので、どの公式をどうやって使うか訓練ができるんだ
 AKINORI
AKINORI
出した結果は小問の答えになっていることが多い

このようにできるところまで導いておくと、小問を見たときにどうですか?
あ!求めたものが問題の答えになってる!!
 AI
AI
当たりまえですよね。最初の設定から小問が作られるわけですから、あらかじめ状況設定の中で解けていればそれが小問の答えになるわけです。
今回は(2)のグラフは解いていませんが、これは小問を見たときに改めて解けばいいだけです。
しかもグラフを書く情報はすでに完成しているので、その通りにグラフを書くだけでおしまいになります。
これが問題集をやっていくうえで使える最強の勉強法であり、見ての通り、実際の試験でも使える解き方でもあるんです!
これはどの分野でも使えます。
解いていくうちに今回のように「熱力学なら2大公式を使おう」のような、必勝パターンが見えてきますよ。
まずは1週間やってみよう

いかがでしたか?
もちろん小問を読みながら解く方が実際は楽です。試験本番で時間と戦うのであればそちらの方が早いです。
また、この方法が本当にあなたに合うかどうかは分かりません。
しかし、勉強法を模索しているのだったらまずは1週間これを徹底してやってみてください。絶対に変化があります。
文字だけだと分かりにくかったと思いますので最後に動画でまとめておきました確認してください。








