透明板(薄膜)を使ったヤングの実験。明線がずれるのはなぜ?

透明板(薄膜)を使ったヤングの実験の問題が解ける
明線がどのようにずれるかが分かる
こんにちは。受験物理setupのあっきーです。
最近、こんな質問がきました。
ヤングの実験で透明板や薄膜を使ったとき、「明線がどちらにどれだけずれるか?」
という問題が解説読んでも理解できません。解説してもらえませんか?
これについて調べてもあまりいい解説がネットにも参考書にもなかったので、多くの人が同じ悩みをもっているんだと思います。
ですが、安心してください。実は、透明板を置こうが何をしようが、全く同じことをやればいいのです。
なぜなら、これはヤングの実験に過ぎないので、光路差を求めて干渉条件を求めれば解けるからです。
一つ違うところは、自分で導いた式を見て適切な解釈ができるかどうかが試されるところです。
この記事では、透明板(薄膜)のあるヤングの実験の問題において干渉条件をどのように導き、どのように式を解釈するかを教えていきます。
これを最後まで読むことで、ヤングの実験で透明板を置いたときに明線がどのようにずれるかを理解できるとともに、干渉問題を楽々解くことができます。
目次
ヤングの実験とは?

ヤングの実験は、ヤングさんが光の性質を調べるためにおこなった実験です。
光の干渉に関するもので、入試でもこれに関する問題が多く問われます。
今回のように透明板を使ったりスリットを動かしたりして応用力を問われることがかなりあります。
ヤングの実験に関して詳しく知りたい人はこちらで説明しているので見てくださいね。
透明板のあるヤングの実験
間隔\(d\)の複スリットA,Bに, 垂直に波長\(\lambda\)の同位相のレーザー光を当てたところ、スリットから\(l\)離れたスクリーン上に明暗の縞が観察された。次に、スリットBのスクリーン側を厚さ\(a\)、屈折率\(n > 1\)の透明な薄膜で覆ったところ、スクリーン中央(O)の明線の位置がずれた。中央の明泉はどちら側にどれだけずれたか答えよ。OはABの垂直二等分線とスクリーンとの交点であり、\(d,a\)は\(l\)に比べて十分に小さいものとする。
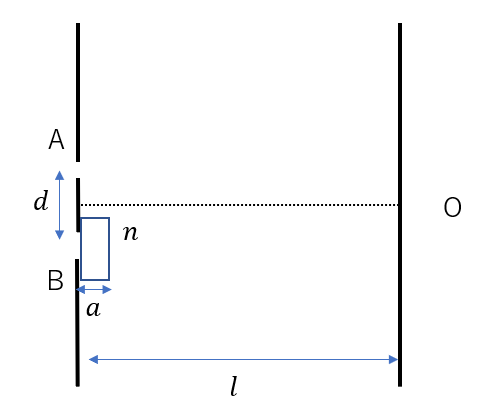
(セミナー物理 2016 発展例題34)
これはヤングの実験、もっと言えば光の干渉の問題です。
なのでやることは干渉条件を求めて、その式を適切に解釈する
たったこれだけです。
干渉条件を求める

まずは、干渉条件を求めます。
干渉条件の詳しい解説は下の記事で説明していますので、見ておいてください。
経路差ではなく光路差を求める
ただ、今回は一つ注意点があります。
スリットBには屈折率\(n\)の薄膜があります。
上の記事で紹介した干渉条件というのは、同位相で空気中の場合に成立する条件式です。
今回の場合、一部薄膜に覆われているので条件式をそのまま使うことができません。
そこで使うのが「光路差」です。
水やガラス、油などの空気以外の中を進む場合は、一度空気中に戻してから考えます。これが光路差というものです。
光路差に関する話はこちらで説明していますので、確認してくださいね。
薄膜があるときの干渉条件とは?
今回は、原点Oの下側に動いたと仮定して考えます。
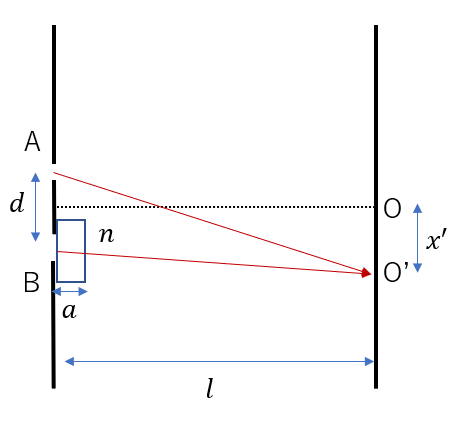
図のように、原点Oから\(x’\)だけ離れた場所における干渉条件を考えます。
光路差を考える必要がありますが、Bから出た光が注意ですね。
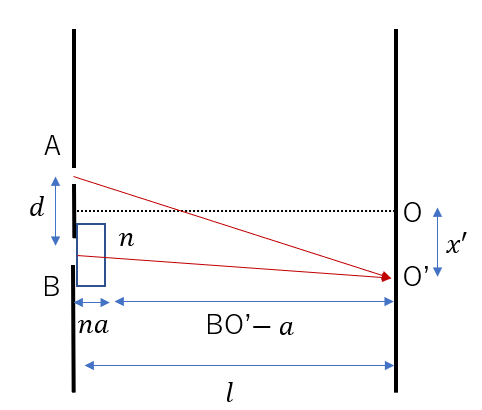
まず、薄膜内にある部分の光路長が\(na\)です。
そして、空気中にある部分はBO’のうち、薄膜の厚さ\(a\)を除いたBO’\(- a\)となります。
厳密には、薄膜に対して垂直に光が進むわけではないので\(na\)とは表せないのですが、\(a\)は\(l\)に比べて十分に小さいので、垂直に進んでいると考えてもOKです。
つまり光路差はこうなります。

このAO’ – BO’は透明板がないときのヤングの実験の経路差と同じなので、
\(\frac{dx’}{l}\)と表すことができます。
つまり、今回の場合の干渉条件は次のようになります。
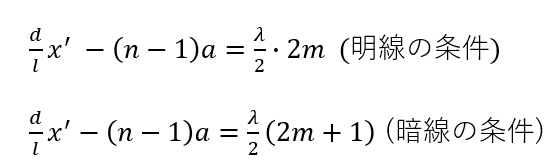
式を見て判断せよ

ここまではいつも通りです。
応用問題で必要なスキルは、この式から必要な情報を適切に読み取ることです。
これはこの問題に限ったことではなく、すべての問題に共通することです。
今回求めたいものは、「薄膜が無い状態で原点Oにあった明線がどちらにどれだけ動いたか」です。
この原点Oにあった明線は0次の明線、つまり\(m = 0\)の明線なわけです。
ということは、今求めた、薄膜ありの明泉の条件式に\(m = 0\)を代入して、\(x’\)を求めればずれた距離がわかりますね。
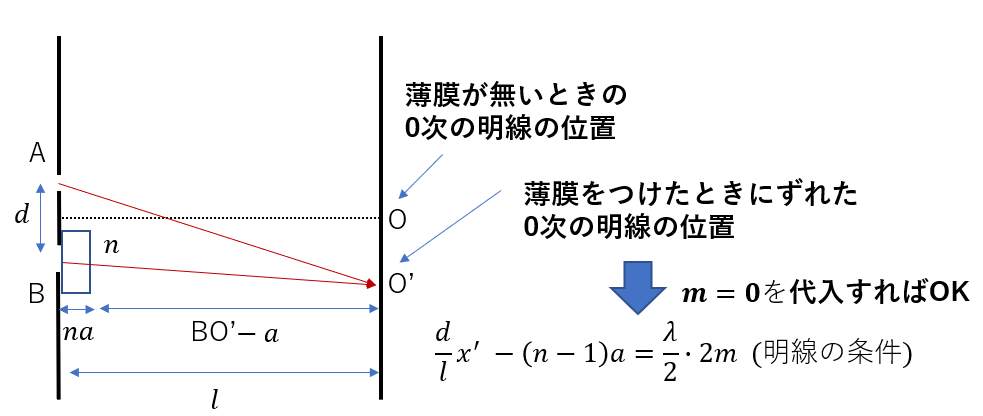
よって\(m = 0\)を代入して\(x’\)を求めるとこうなりますね。
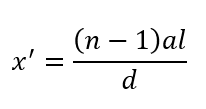
\(n > 1\)なので、\(x ‘ > 0\)
つまり、最初に仮定した通り、下向きにこれだけずれると求めることができました。
最初に上向きにずれると仮定したらどうなるんですか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
その場合は、マイナスで答えが出ます。マイナスということは逆向き、つまり下向きだったとなるので、答えは一緒になります。
 あっきー
あっきー
スリットを動かす場合も同じ!

このように、薄膜や透明板があっても干渉条件を求めて式を的確に解釈することができれば解けてしまうのです。
この干渉縞がずれる問題は、スリットを動かす場合にも起こります。
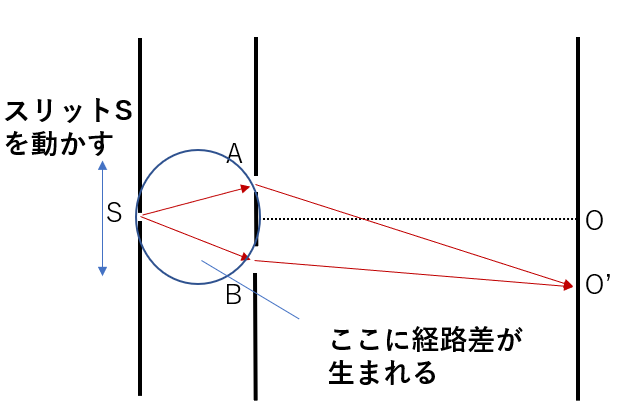
この場合も同じで、SAとSBの間で経路差が生まれて、その分干渉条件が変わって、そこから縞がずれるというのが分かります。
やってることは今回の問題と特に変わりはありません。
ぜひ、これを元に自分の力で問題を解いてみてください。
まとめ:慣れないことはするな!

いかがでしたか?
今回はヤングの実験の応用編でした。
今までと状況が変わると、今までやったことのない方法で考えたり、解こうとする人が多いです。
ですが、あくまでヤングの実験です。あくまで光の干渉問題です。
ですから、「経路差(光路差)を求めて干渉条件を使う」という本質的な部分は変わらないのです。
応用問題では、その出した式からしっかり情報を読みとれるかというところを深く問われているだけなのです。
難しく考えず、できることをやるだけです。
透明板のあるヤングの実験
基本は「光路差を求めて干渉条件を導く」
→その式から必要な情報を読みとる訓練をしておこう!








