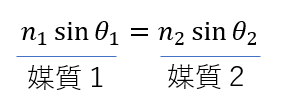光の屈折の法則の簡単な覚え方!見た目が100%?

屈折の法則の導出方法が分かる
屈折の法則(スネルの法則)の意味が分かる
こんにちは!オンライン塾を運営している、あっきーです
 あっきー
あっきー
屈折の法則の導出が分からない!
屈折の法則が覚えられない!
 リケジョになりたいAIさん
リケジョになりたいAIさん
このような悩みはありませんか?
実は屈折の法則(スネルの法則)の公式を簡単に覚える方法があります。
それは図を見たまま屈折の法則を公式にするというものです。
今回は、屈折の法則の導出を分かりやすく教えていき、結果の絶対に忘れない方法を教えたいと思います。
この記事を最後まで読むことで、薄膜干渉など、光の干渉の問題を楽々解くことができるようになります。
目次
波の屈折とは?

まず、屈折というのが何か説明していきます。
例えば、空気中から水中に向かって光を照射するとどうなるかイメージできますか?
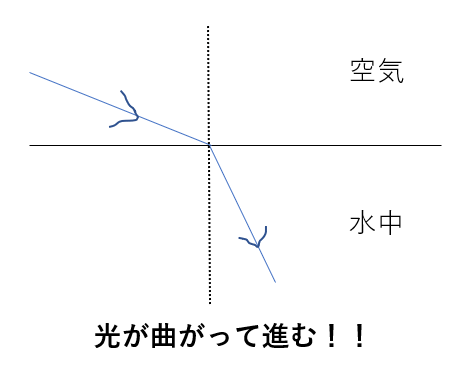
境界で曲がりますよね。
波は無数の物質が振動することによって起こるのでしたね。
つまり、波は媒質の種類で伝わり方が変わるってことです。
媒質が変われば当然ながら
波の伝達速さも変わるでしょうし
波長も変わるでしょう。
さらに、図のように進む方向も変わってきます。
この波の速さや波長、そして角度に関して
どんな関係があるの???
というのを導いてみましょう!
今回は光で考えますが、この話はすべての波に共通するものです。
そもそも屈折が起こる理由を知りたい方はホイヘンスの原理をご覧くださいね。
屈折の法則(スネルの法則)を導出しよう

媒質1において、光の速さ、波長は\(v_1, \lambda_1\)であり、この光が入射角\(\theta_1\)で媒質2に入射する。光は媒質2では、速さ、波長がそれぞれ\(v_2, \lambda_2\)であり、屈折角が\(\theta_2\)であった。これら物理量に関して成り立つ式を導け。
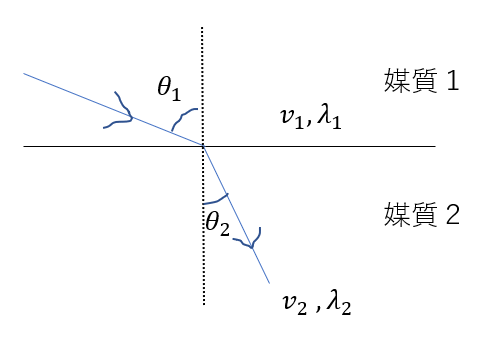
速さと入射角・屈折角の関係

まず、媒質1,2のそれぞれの速さと角度の関係を調べてみます。

今、経路が違う二つの平行な光があります。
これらは経路が違うだけで、速さや波長は同じ光であり、同位相です。
ここで、1秒間で
- 光1はAからBまで
- 光2はBからB’まで
動くいたとしますね。
つまり、
\(AB = v_2\)
\(A’B’ = v_1\)
となります。
また、垂線AA’, BB’を引くと
\(\angle A’AB’ = \theta_1\)
\(\angle AB’B = \theta_2\)
となります。
さて、△AA’Bと△ABB’を見るとそれぞれで次のような関係式が立てられるますよね。
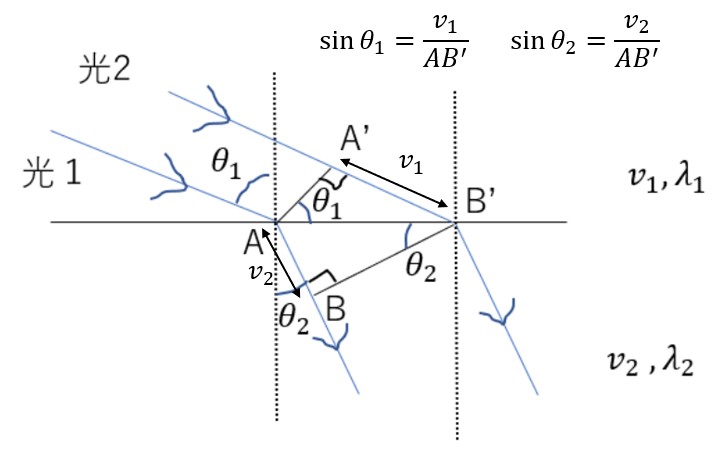
この二式から、AB’を消去すると次の関係が得られますね。

このように速さを角度の関係式を求めることができました。
速さと波長の関係を導出する

次は、速さと波長の関係を考えましょう。
速さと波長と言えばこの関係式しかありませんね。
\(v = f\lambda\)
これです。
これは波の個数を表した公式です。
詳しくは波の基本式の記事を見てくださいね。
\(f\)がその波の個数を表すのですが、「1秒間に現れた波の個数が\(f\)」となります。
波の個数はある点の振動の回数が問題なのですが、媒質によって振動の回数は変化しません。
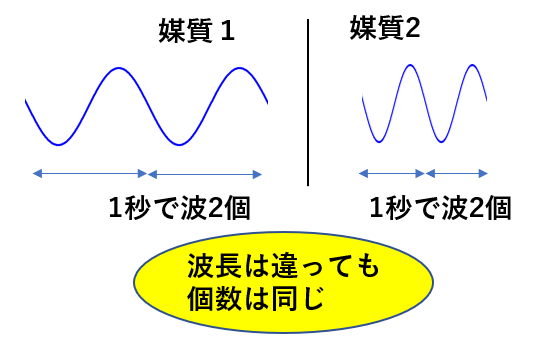
どの媒質に進もうが、
波の個数が変わるわけがないのです。
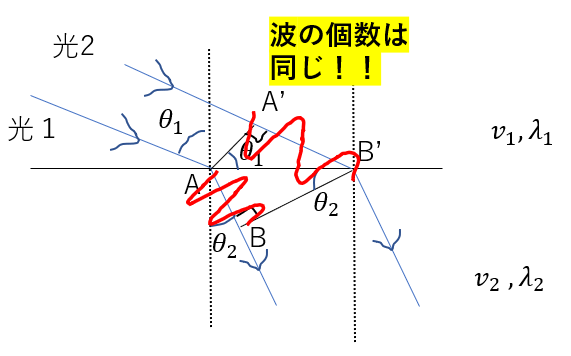
つまり、AB間の波の個数とA’B’の波の個数は同じに\(f\)となるのです。
後は波の基本式を使って、
\(v_1 = f\lambda_1\)
\(v_2 = f\lambda_2\)
このように表せるので\(f\)を消去すると次の関係が得られますね。
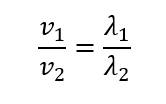
このように、速さと波長の関係も得ることができました。
屈折の法則の公式は図をそのまま式にする

以上をまとめるとこのように表せますね。
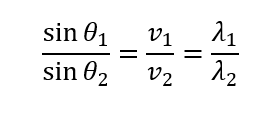
これが屈折の法則(スネルの法則)です。
ただ、「これを声に出して暗記してください~」
なんていうのはあまりにも酷なので、絶対に忘れない覚え方を伝授したいと思います。
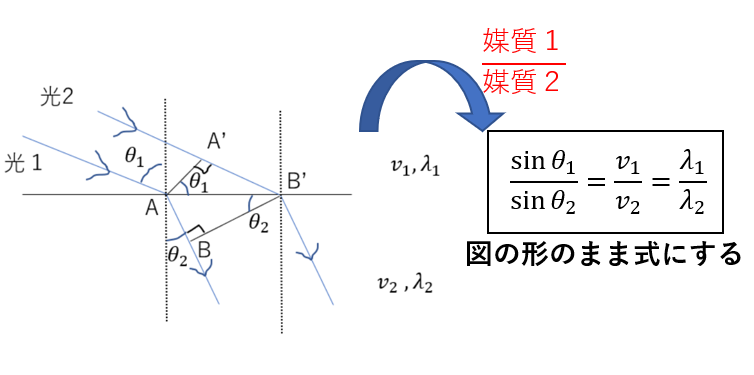
このように図の形をそのまま式に表した関係になっていますね。
このように覚えれば絶対にわすれませんね。
屈折率を使った関係式

もう一つ、この式に屈折率の情報を追加したいと思います。
屈折率というのは、「どれだけ屈折するか」という屈折の度合いを表します。
ただ屈折には、必ず二つの媒質が必要なので
ある媒質を基準に、どれだけ屈折するか?
というように、相対的に考える必要があります。
問題文で出てくる「屈折率を\(n_1,n_2\)とする」というこの\(n_1,n_2\)は空気に対する屈折率です(絶対屈折率とも言います)。
つまり、空気の屈折率を1と定めたとき、媒質の屈折率それぞれ
\(\frac{n_1}{1} = n_1\)
\(\frac{n_2}{1} = n_2\)
となるわけですね。
そして、「媒質1に対する媒質2の屈折率\(n_{12}\)」はこのように定義されます。
\(n_{12} = \frac{n_2}{n_1}\)
「媒質1を基準にする」ということですから、\(n_1\)が分母にきます。
これを使って屈折の法則はこのように表すことができます。
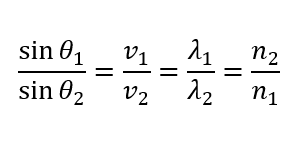
あれ?屈折率のところだけ数字が逆になってる。。。
 リケジョになりたいAIさん
リケジョになりたいAIさん
これは屈折率の定義から表されるので、これはどうしようもないです。
 あっきー
あっきー
先ほど図の形のまま、分母分子を並べてイコールをつなげればいいとお話をしました。
ですが、屈折率に関してだけはこれが通用しなくなってしまいます。
これはイレギュラーすぎるので、屈折率を使う場合はちょっと変形しましょう!
例えば、角度と屈折率だけを見ると、次のように変形できますよね。
\(n_1\sin{\theta_1} = n_2\sin{\theta_2}\)
つまり
(媒質1)=(媒質2)
と捉えることができます。
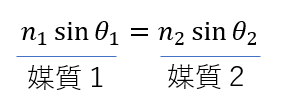
このように、考えれば覚えやすいと思います。
まとめ:屈折の法則の公式は図で覚える

いかがでしたか?
もちろん屈折の法則を一度は導出してください。
その後、覚える際は図と関連付けて覚えることをオススメします。
屈折の法則

*屈折率を使う場合は以下のように覚えよう