回折格子とは？透過型と反射型の回折格子を分かりやすく解説！
どうも！オンライン物理塾長あっきーです
あっきー
回折格子を学校で全然やってくれなくて困ってます！助けてください。
リケジョになりたいAIさん
回折格子で悩んでいませんか？
「なんで明線の条件しかないの？」
「なんで隣り合う光だけで干渉条件出してるの？」
「反射型の回折格子意味わからん！」
「スリット間隔が異なるときどうするの？」
もしこのような悩みがあるならこの記事を読んでください。
この記事では、回折格子の特徴を押さえつつ、問題の解き方を教えていきます。
最後まで読むことで、入試レベルの回折格子の問題が解けるようになります！
回折格子の原理が分かる
回折格子で明線の条件しか出さない理由が分かる
反射型の回折格子の扱い方が分かる
スリット間隔が異なるときの対処法が分かる
目次
回折格子とは？
ヤングの実験を思い出してください。
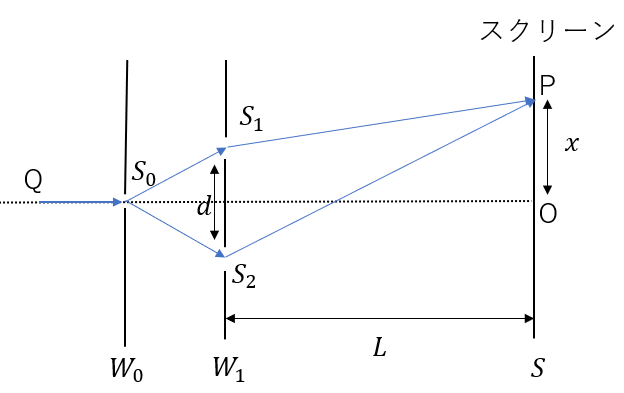
ヤングの実験ではこのようにスリットが二つあって、このスリットによって二つの光が干渉が起こります。
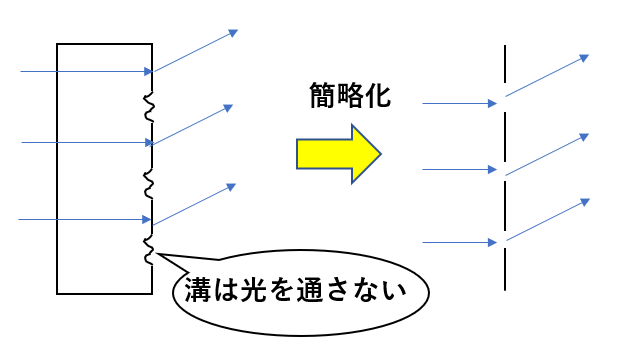
スリットは2つだけでなく、複数あっても光の干渉は起こります。
多数のスリットが一定間隔で並んだものを回折格子と呼びます。
回折格子は2パターン出る
もちろん光の干渉ということなので、干渉条件を求めてみます1つ注意があります。
実は回折格子は2パターンあるんです。
透過型
反射型
この二つです。圧倒的に透過型の方が多いですが、入試でたまに反射型の回折格子が出される場合があるのでそれも確認してきましょう。
透過型の回折格子
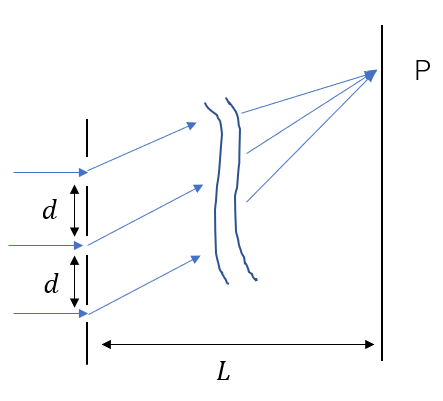
透過型は先ほど見せたものです。
そして、原理はヤングの実験の場合と何も変わりません。スリットが2つから多数になっただけです。
回折格子はスリットが等間隔に並んでいます。この間隔を\(d\)（これを格子定数と呼ぶ）、スクリーンまでの距離を\(L\)とすると、\(L\)は\(d\)に比べて十分に大きいです。
ですから、各光は平行とみなしてよいです。
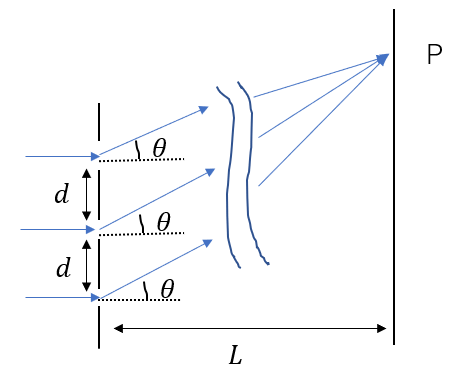
つまり、このように各光の水平線からの角度を\(\theta\)と置くと、隣り合う光の経路差は\(d\sin{\theta}\)と表すことができます。
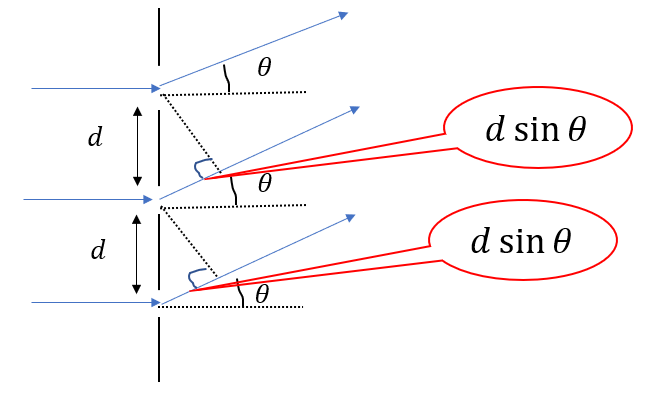
ということで、隣り合う光が強め合う・弱めあう条件は次のように表すことができます。
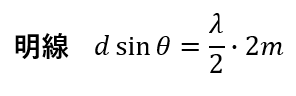
明線しか条件を出していませんが、その理由は後程説明します。
回折格子は原則に隣り合うものを見ればOK
これはあくまで隣り合う光の干渉条件です。実際は多数の光があるので、各組で干渉条件を立てなければいけません。
先ほどの図では一番上と一番下の干渉条件も本来であれば考える必要があります。
しかし、回折格子では隣り合う光だけを考えれば良い場合が多いです。
回折格子のスリット間隔\(d\)は非常に小さくかつどこを取っても同じです。またスリット幅は無視できるくらい小さいです。
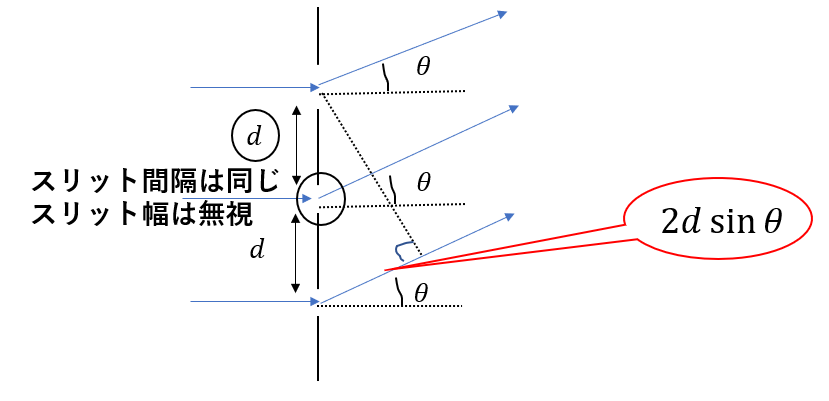
つまり、一番上の光と一番下の光の経路差は\(2d\sin{\theta}\)と表せて、同様に干渉条件を出せますね。
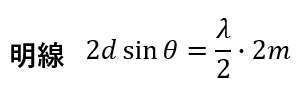
・・・何かにきづきませんか？
先ほどの隣り合う光の条件式と合わせて見てみましょう。
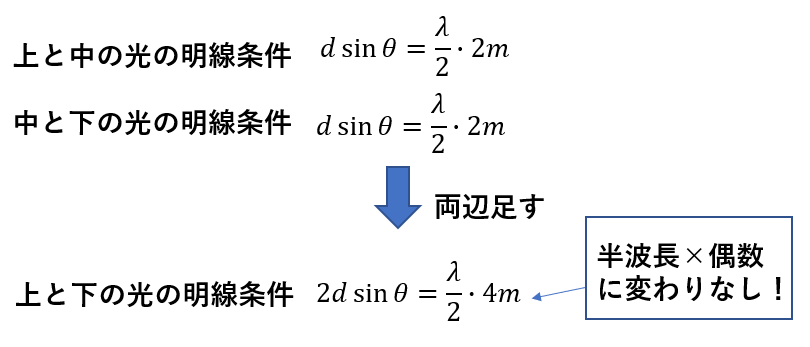
上と真ん中、真ん中と下がそれぞれで強め合っていれば、上と下でも自然と強めあうことが式から分かるのです。
スリットの数を増やしても同じで、隣り合う光だけ考えれば、どの光の組み合わせでも強め合うのです。
教科書などで隣り合う光だけで干渉条件を考えていたのはこのためです。
ただし、これには条件があります。
- スリット間隔\(d\)がどこを取っても同じです。
- スリット幅は無視できるくらい小さいです。
最初に原則と強調したのはこのためです。
スリット間隔が異なる場合は？
スリット間隔が異なる場合はどうなるんですか？
リケジョ志望のAIさん
もちろん、今やったようにとなり合わない光についても考える必要があるんだ。
オンライン物理塾長あっきー
これについては最後にやる問題演習で解説します。
スリット幅が大きいときは
では、スリット幅が無視できな場合はどうなるんですか？
リケジョ志望のAIさん
その場合は、単スリットというのを考えないといけないんだ。
オンライン物理塾長あっきー
ここまでは、複数のスリットを使うことで光の干渉を見てきました。
ですが、実はスリットが１つしかなくても干渉は起こるんです。
スリット幅が無視できない場合は、各スリット単体で起こる干渉と各光が重なることで起こる干渉を同時に考えないといけません。
これは複雑すぎるので入試にはまず出ません。
しかし、「単スリット」の問題は問われます。これについては別の記事で解説しますね。
反射型の回折格子
入試では反射型の回折格子も問われます。
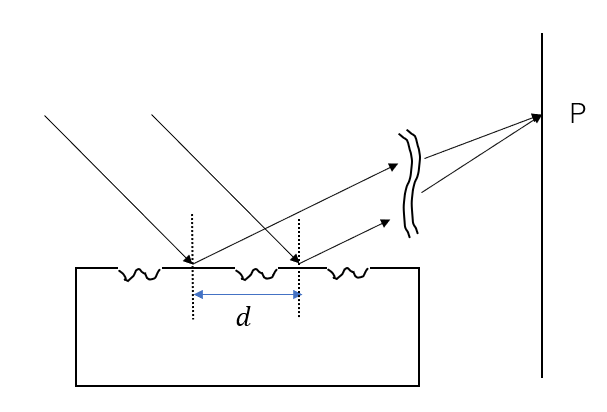
透過型と同じで、回折が起こります。
本来なら入射角と反射角が同じになるように反射します。
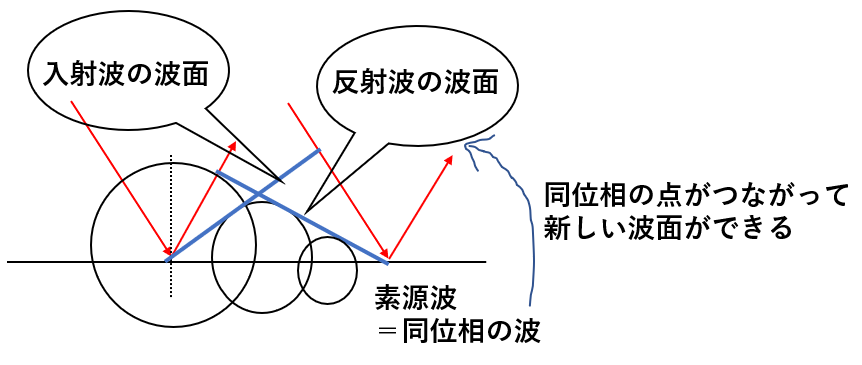
ホイヘンスの原理からある波面が入射すると反射面から素源波が生まれます。
素源波を円で表していますが、この円周上の点はすべて同位相の点です。
また、同位相の点をつなげたものを波面と呼びます。
つまりある入射波が平面に当たってはね返った波面を探すには、素源波の重なった部分をつないだところになります。
図では素源波は3つしか書いていませんが、本来は無数にあります。無数に円を描いたら、円の接線で繋がるのがイメージできますね。
この時、たまたま入射角と反射角が同じ大きさだったということです。
ですが、回折格子には溝があります。溝がある部分では乱反射が起こってしまい、光があちらこちらに光が反射してしまいます。
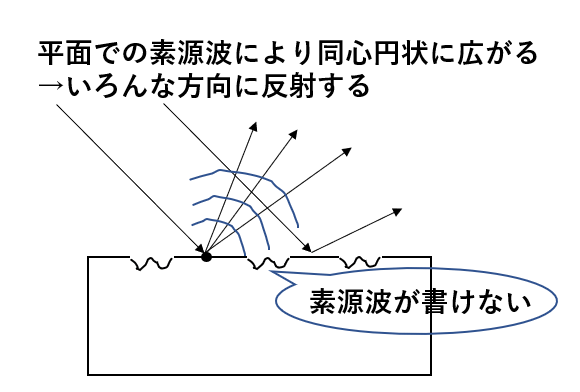
溝の部分に入射した光（波面）について素源波が書けません。円の接線を書くことができず、先ほどのように一直線に進む波面はできないのです。
平面で生まれた素源波によって光は図のように同心円状に広がる、つまり回折するのです。
ちょっと複雑ですね。
反射型回折格子の干渉条件
この場合の干渉条件は透過型と同じように導けます。
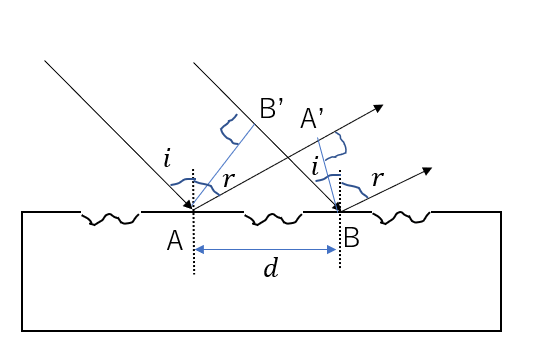
入射角が\(i\)となるように光を入射します。そして反射角が\(r\)とします。このとき二つの光は平行とみて良いです。
なので、入射光において垂線AB’より前、反射光において垂線A’Bより後は経路差がありません。
つまり、考える経路はAA’とBB’となります。
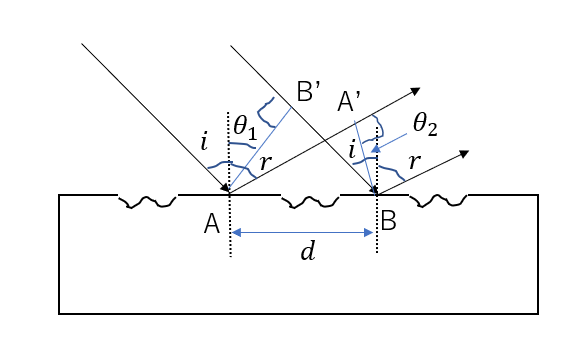
図のように\(\theta_1, \theta_2\)を取ると、
\(i + \theta_1 = 90^\circ, \theta_1 + \angle B’AB = 90^\circ\)となるので
\(\angle B’AB = i\)と表せます。
また\(r + \theta_2 = 90^\circ ,\theta_2 + \angle A’BA = 90^\circ\)と表せるので
\(\angle A’BA = r\)となります。
なので
\(AA’ = d\sin{r}\), \(BB’ = d\sin{i}\)
と表せます。
経路差はこれの差を取ればOKです。（大小関係が分からないので絶対値をつけておきます）。
\(|AA’ – BB’| = |d(\sin{r} – \sin{i})|\)
これを使って干渉条件を立てれば良いですね。
明線条件しか出さない理由→ヤングの実験と回折格子の違い
さっき、回折格子で明線の条件しか出さない理由があるって言ってましたよね？あれを教えてください！
リケジョ志望のAIさん
あれは、回折格子の特徴を理解できれば分かるよ。
オンライン物理塾長あっきー
回折格子とヤングの実験はほとんど同じなのに、回折格子は明線の条件を考えませんでした。
それはスクリーンに現れる干渉縞に理由があります。
ヤングの実験では明線がはっきりしない
ヤングの実験ではスリットが2つしかありませんでした。スリットが2つだけではスクリーンに明暗がはっきりとは現れません。なぜなら明線の条件から少し外れても、ぼんやり強め合うからです。
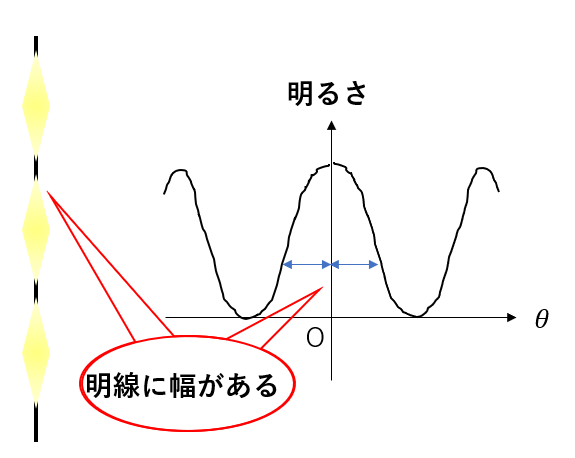
明線がはっきりしないので、何か測定をする際には暗線を用いた方がより精度が高くなります。なので暗線条件も求めました。
回折格子では明線がはっきりする
回折格子では、多数のスリットがあります。多数のスリットがあると、先ほど見たようにいろんな組の明線条件を考えなければいけません。ですから、明線になる条件はかなりシビアになります。
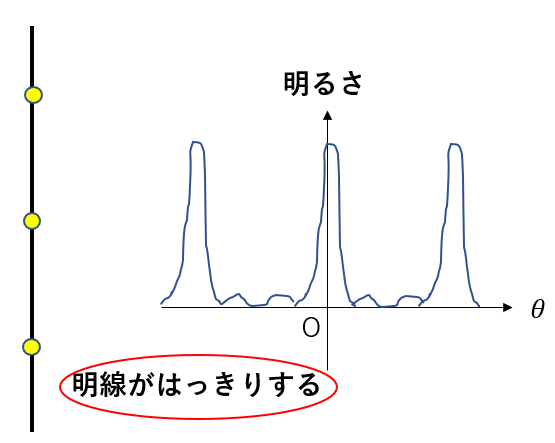
特定の部分だけはっきり明るくなり、少しずれると一気に暗くなります。
ですから、明線がはっきりして暗線はわかりにくいです。
なので、回折格子では明線の条件だけ考えれば良かったのです。
回折格子の問題
では、最後に回折格子の問題をやって終わりにしたいと思います。
図1に示すように、スリットの面に垂直に、波長\(\lambda\)の平面波の光を入射する。スリットは紙面に垂直な方向に十分に長く、またその幅は小さいため、スリットを通過した光は解説によって広がり、紙面上で円形波とみなせる。
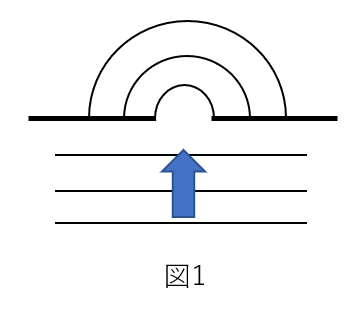
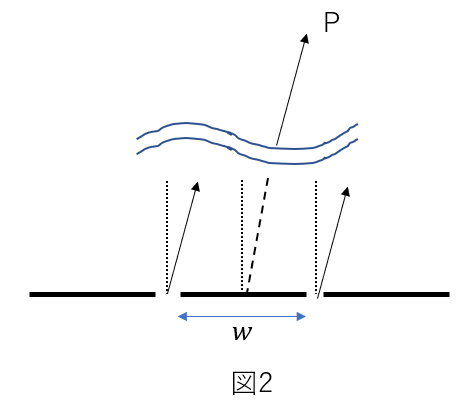
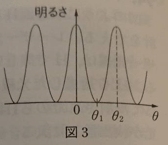
(1) 図2のようにスリットを2つにしてその幅\(w\)とする。スリットの面に垂直な方向から角度\(\theta\)の方向に距離\(R\)だけ離れた観測点Pにおける明るさを\(\theta\)を変えながら測定したところ、図3のようになった。このとき、\(\sin{\theta_1}, \sin{\theta_2}\)の値を求めよ。ただし、\(R\)は\(w\)より十分起大きいものとする。
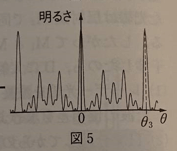
(2) 図4のように、スリットの数を5本に増やし、スリット間隔を\(60d, 30d, 45d, 45d\)にした。(1)と同様に観測したところ図5のようになった。このとき、\(\sin{\theta_3}\)を求めよ。
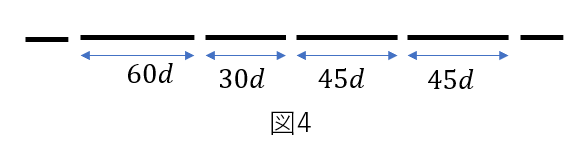
（重要問題集2019 問95）
(1) ヤングの実験です
(1)はそこまで難しくないですね。ヤングの実験そのものです。詳しくはヤングの実験の記事を読んでください。
干渉条件はこのようになります。
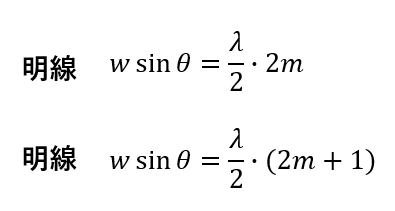
そしてグラフを見ると\(\theta_1\)は1つめの暗線、\(\theta_2\)は2つ目の明線となる場所ですね。
つまり\(\theta_1\)には0次の暗線、\(\theta_2\)には1次の明線が現れます（\(m=0\)から数えるので注意です）。
まず\(\theta_1\)に関しては
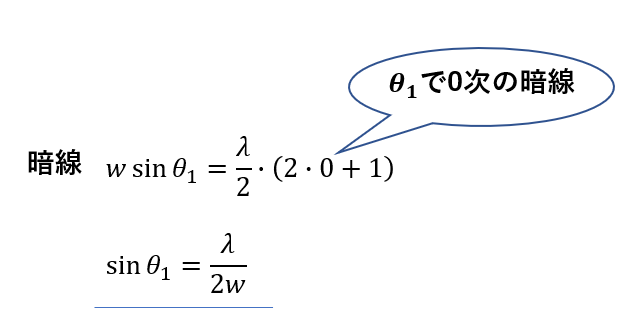
\(\theta_2\)に関しては
このように表せます。
(2) 隣り合う条件・・・だけではだめ！
今回の最大のポイントです。
まず、グラフがいびつですが、これが起こる理由はスリット間隔が一定ではないからです。強め合う光と弱めあう光が出てくるので、ぼんやり明るい部分が出てしまうんですね。
そして、\(\theta_3\)の位置では飛び抜けて大きくなっています。これはすべての光が強め合っているということを表しています。
その条件を求めれば良いのですね。
スリット間隔が一定ない場合、各組の干渉条件をすべて考えないといけません。
でも、それは時間がかかりすぎます。なので裏ワザを使います。
最も大きくかつ等間隔になるよう仮想的に分解するです。
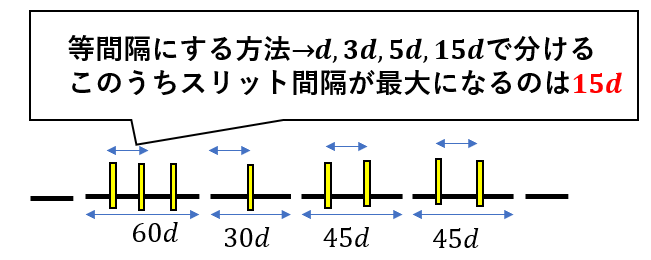
等間隔になれば、先ほど見せたように隣り合うもの同士を考えるだけで、それがすべての光が強め合う条件になります。
等間隔に分ける方法はスリット間隔の公約数で区切れますよね。そのなかでも最大公約数を使って区切ります。
すると、干渉条件はこのように表せますね。
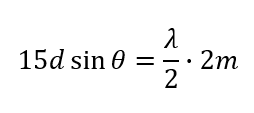
\(\theta_3\)では、2つ目の明線になりますから\(m=1\)とすれば答えが出ます。
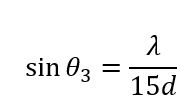
これが答えです。
このように、スリット間隔が異なる場合には
最も大きくかつ等間隔になるよう仮想的に分解して対処しましょう。
まとめ
いかがでしたか？
回折格子をがいまいちわかってなかった人はこの記事で理解できましたか？
もしそうであればうれしいです。
それでは！
