単スリットとは?回折が起こる理由と干渉条件の求め方を分かりやすく

どうも!オンライン物理塾長あっきーです
 あっきー
あっきー
光の干渉の問題でヤングの実験や回折格子のように複数のスリットを使ったものをやってきたと思います。
なので、スリットが複数ないと干渉が起こらないと思われている人が多いです。実は単スリットでも起こります。
単スリットの問題が問われることもありますが、一度触れておけば間違いなく解けます。それくらい簡単です!
この記事では、単スリットの性質と干渉条件の求め方、そして単スリットの問題の解説します。
最後まで読むことで単スリットの理解がつき、入試問題も解けるようになります!
単スリットの性質が分かる
単スリットの干渉条件が分かる
単スリットの入試問題が解ける
目次
単スリットとは?

単スリットは、名前の通りスリットが1つだけの干渉を考えるものです。
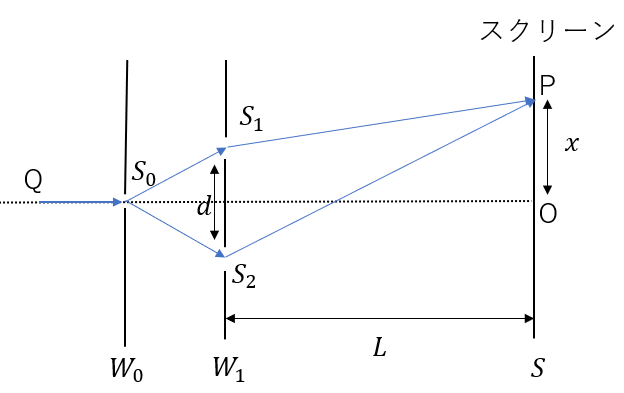
ヤングの実験ではこのように2つのスリットを通して干渉を考えていました。
ヤングの実験ではスリットの幅をめっちゃ小さくしていましたが、スリットの幅を広げるとどうなるでしょう?
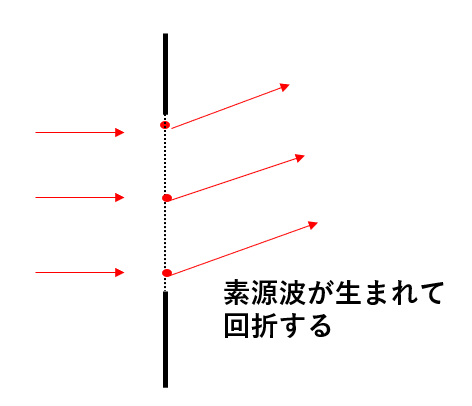
このように、スリットでいくつかの素源波が生まれます。これにより解説が起こり、干渉が起こるのです。
今まではスリットの幅がものすごく小さく、1つのスリットごとの干渉は考える必要がありませんでしたが、幅を持ったスリットではそのスリットに関して起こる光の干渉を考える必要があるのです。
単スリットの干渉条件

この単スリットの干渉条件を求めましょう。
暗線が見える場合
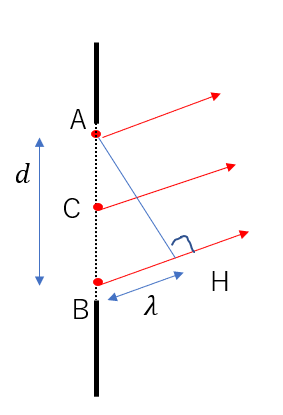
Aから出た光とBから出た光の経路差が\(\lambda\)だとします。
この時ABの中点をCとするとAの光とCの光の経路差は\(\frac{1}{2}\lambda\)となります。
半波長の奇数倍になっているのでAとCの光は弱めあいます。
AとCと同じ間隔であらゆる点から出る光について見ていきます。
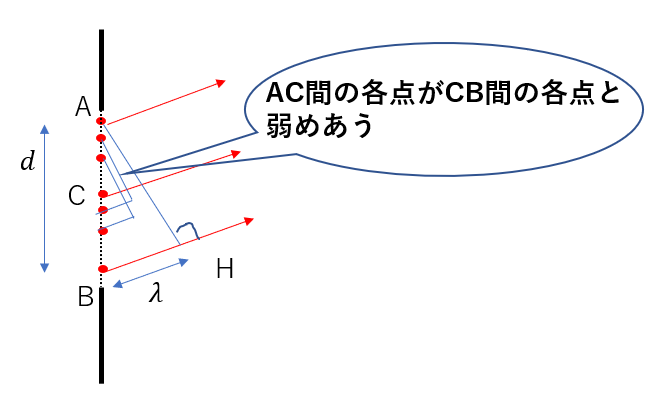
AとCから少しずらした点もまた弱めあい、また少しずらした点も弱めあい・・・
と続けていくと最終的にAC間の各点はCB間の各点と弱めあいます。
つまり、このとき暗線が現れるのです。
明線が見える場合
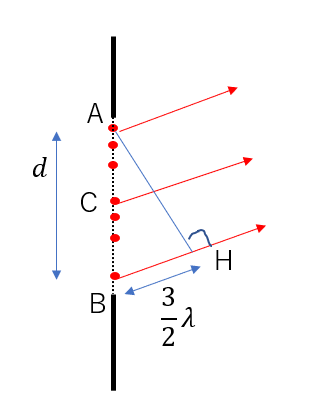
今度はACの経路差が\(\frac{3}{2}\lambda\)の場合を考えます。
今度はAB間を3等分してみましょう
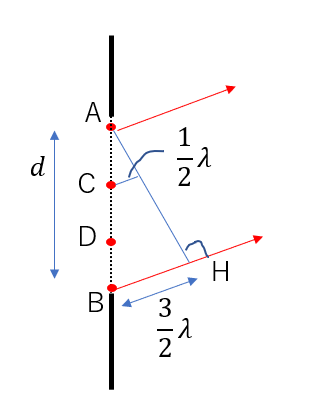
AとCから出る光は経路差が\(\frac{1}{2}\lambda\)なので弱めあいます。
先ほどと同じように、AとCから下に少しずらした点も弱めあい・・・と考えていけば、AC間の各点はCD間の各点と弱めあいます。
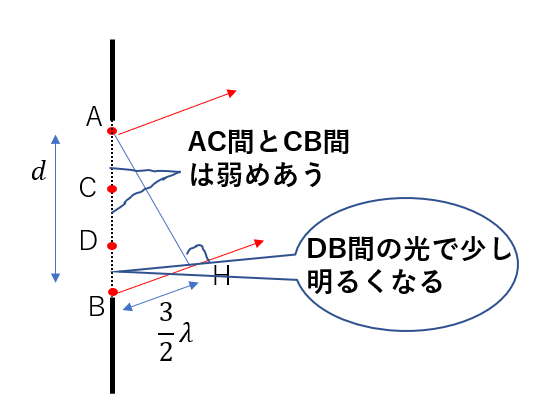
この場合ではDBの光が打ち消されておらず、この区間の光によってぼんやり明るく見えます。
暗線の条件

今、経路差を特定して考えていました。
しかし、AとBの経路差が\(\lambda, 2\lambda, …\)となれば暗くなりますし\(\frac{1}{2}\lambda, \frac{3}{2}\lambda, …\)とすればぼんやり明るくなります。
つまり、一般的に暗線の条件を求めることができます。
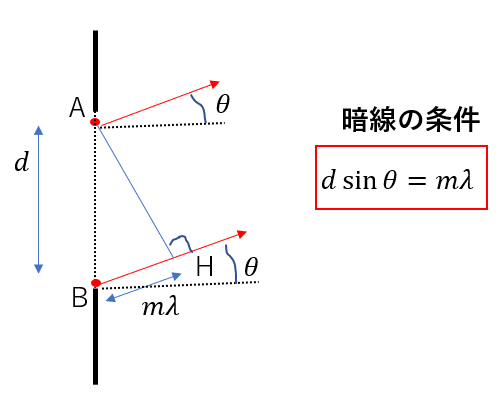
このように\(d\sin{\theta} = m\lambda\)のとき暗くなるということが分かります。
暗線の条件だけでOK

単スリットでは明線の条件式は必要ありません。
単スリットではスクリーンに次のように干渉縞が表れます。
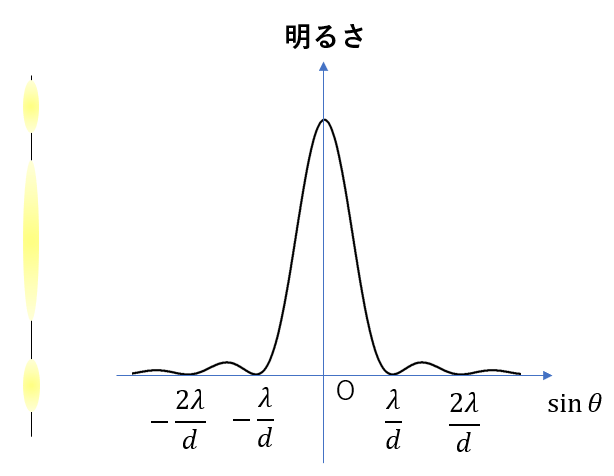
回折格子のところでもお話しましたが、スリットが多いと条件がシビアになります。
今回は1つのスリットしかありませんし、スリット幅が比較的大きいので干渉条件から少し外れても明線が現れます。
なので、このように明線に幅が生まれます。
暗線の方がピンポイントで分かるので暗線の条件だけで良いのです。
ちなみに、明るさは原点から外れると急激に小さくなります。これも単スリットの特徴です。
ヤングの実験で単スリットを広げると?

この明線が広がるという話は、ヤングの実験でも適用できます。

最初のスリットS0は単スリットです。ヤングの実験ではこのスリット幅は無視できるくらい小さいですが、その状態から広げると、スリット内でも経路差が生まれます。
そのため、S0のスリットのみで起こった干渉がスクリーンに映るため明線が広がるのです。
単スリットの問題

では最後に単スリットの問題を解いて見ましょう。ちなみにこの問題は回折格子で紹介した問題の続きなのでそちらの問題を読んでから解いた方が良いです。問題文も続きからになっています。
次に、スリット幅が無視できない場合を考える。図6のように幅\(D\)の単スリット対し、(2)と同様の測定をしたところ、Pにおける明るさは\(\theta=0\)の付近で図7のようになった。この理由を考えよう。
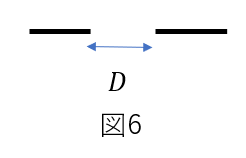
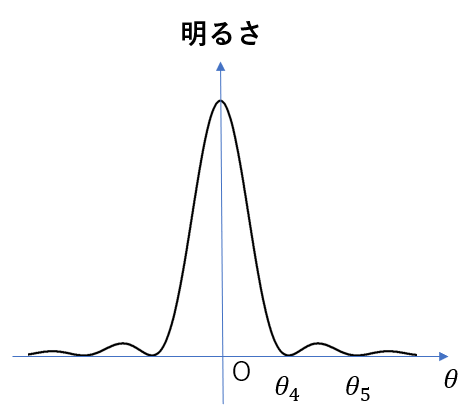
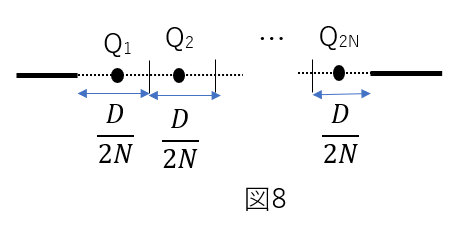
図8のように、スリットを\(2N\)等分して、各区間から素源波が表れて干渉が起こると考えられる。
(3) \(N=2\)のとき、\(\theta\)を0から大きくしていくと、最初に\(\theta_4’\)で、次に\(\theta_5’\)で明るさが0になった。4つの波源を2つずつの対して考えれば、それぞれの波源の対に関して干渉条件が成り立つ。波源の選び方に複数あることに注意して、\(\sin{\theta_4′}, \sin{\theta_5′}\)を求めよ
(4) \(N\)を大きくしていくことで、図7の\(\theta_4, \theta_5\)を求められる。\(\sin{\theta_4}, \sin{\theta_5}\)を求めよ。
この問題は先ほど見てきた内容を問題形式で与えただけです。
この問題で干渉条件を自力で導くことができれば単スリットは完璧です。
(3) 暗線の条件を自力で求めよう
前提知識があれば非常に簡単です。
4つの波源が等間隔に並んでいるので、2組が弱めあえば同じ経路差にある2組弱めあい、結果的にすべての光が弱めあいます。
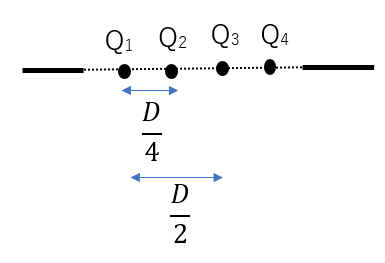
例えばQ1とQ2で弱めあえばQ3とQ4も同経路差になるので弱めあいます。
Q1とQ3が弱めあえば、Q2とQ4も同経路差にあるので弱めあいます。
この2組で考えれば良いんですね。
Q1とQ2が弱めあう条件は
\(\frac{D}{4}\sin{\theta} = \frac{\lambda}{2} \cdot (2m+1)\)
Q1とQ3が弱めあう条件は
\(\frac{D}{2}\sin{\theta} = \frac{\lambda}{2} \cdot (2m+1)\)
それぞれ\(m=0\)として求めればOKです。\(\theta_4′,\theta_5’\)の大小に注意してくださいね。
\(\sin{\theta_4′} = \frac{\lambda}{D}\)
\(\sin{\theta_5′} = \frac{2\lambda}{D}\)
Q1とQ2が弱めあう条件で\(m=0, 1\)で考えればいいように思えますが、\(m=1\)を代入すると
\(\sin{\theta} = \frac{6\lambda}{D}\)となります。
この値はQ1とQ3が弱めあう条件式に\(m=0\)を代入したときの\(\sin{\theta}\)より大きいです。
最も小さいものから\(\theta_4′, \theta_5’\)を求めないといけないので、このような解き方になります。
(4) 一般的に考えればいい
(4)も同じです。一般的に考えるだけです。
どんなに等分しても、偶数個波源ができれば、半分ずつ区切ることですべての点で弱めあいます。
また\(\frac{1}{4}\)で区切ることでも同じように弱めあいます。
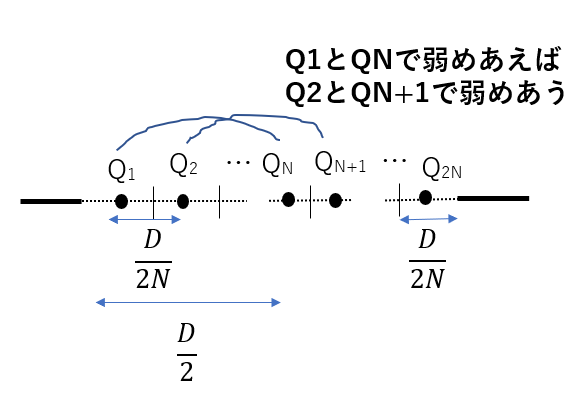
これは結局(3)と同じ状況です。
\(\frac{D}{4}\sin{\theta} = \frac{\lambda}{2} \cdot (2m+1)\)
\(\frac{D}{2}\sin{\theta} = \frac{\lambda}{2} \cdot (2m+1)\)
この二つに関してそれぞれ\(m=0\)を代入しておしまいです。
\(\sin{\theta_4} = \frac{\lambda}{D}\)
\(\sin{\theta_5} = \frac{2\lambda}{D}\)
まとめ:単スリットは前提知識があれば解ける

いかがでしたか?
単スリットは前提知識があれば楽に解けます。単スリットの問題は干渉条件を導出をするものばかりだからです。
一度自分の手で導出して原理を理解しておきましょう。










Comment
結構ミスって書いてる所ないですか?
具体的にどこですか?
(受験生でこのサイトの内容鵜呑みにしたので)