【物理】波のグラフの読み取り方を超わかりやすくまとめてみた
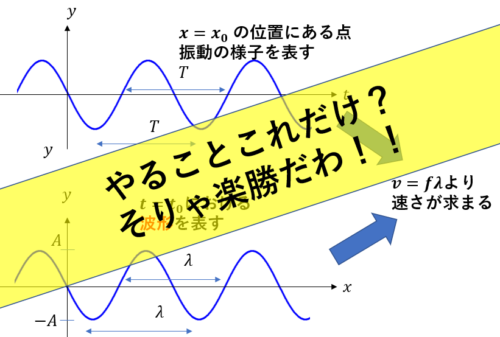
波のグラフの見方が分かる
正弦波の式からグラフを書くことができる
こんにちは!オンライン塾を運営している、あっきーです
 あっきー
あっきー
波のグラフの読み取り方が分からない!
波のグラフを書くことができない!
波のグラフから正弦波の式が表せない!
 リケジョになりたいAIさん
リケジョになりたいAIさん
このような悩みはありませんか?
実は、波のグラフは30分あれば理解することができます。
なぜなら、波のグラフの読み取り方は決まっているからです。
この記事では、波のグラフを読み取り方を分かりやすく教えていきます。y-tグラフy-xグラフがどのように違うのか、そしてグラフを書く方法も教えていきます。
この記事を最後まで読むことで、模試や試験本番でグラフの問題が来ても、1問もミスすることなく解くことができます。
目次
波のグラフはラッキー問題

まず、最初に言っておきます。
波のグラフの問題は非常にラッキー問題です。
グラフが出てきたということは、正弦波の式を与えられたようなものです。
正弦波の式はこのように表されましたね。
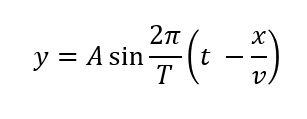
ですから、グラフが出てきたということは、この正弦波の式が与えられたのと同じであり
振幅\(A\), 周期\(T\), 速さ\(v\), 波長\(\lambda\)など、波の重要な情報をすべて読み取ることができます。
波の問題はこれらの情報を正確に読み取ることが大事になってくるので、グラフ問題は重要です。
正弦波の式に関してはこちらを確認してください
2つの波のグラフの違い

あっきーさん。波のグラフて2種類あるじゃないですか?あのグラフの違いって何ですか?なんで二つもあるんですか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
その理由は正弦波の式が教えてくれるよ!
 あっきー
あっきー
波のグラフにはy-tグラフとy-xグラフの2種類がありますね。
なんでグラフが2種類あるのか?あまり気にしていない人が多いですが、結構大事なことです。
もう一度、正弦波の式を見てみましょう。
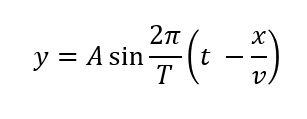
この式の中で変化する情報が3つあります。
\(y, t, x\)ですね。
ですが、平面にグラフを書くとなると軸が縦軸と横軸の2つしか取れないので
このうち2つの情報しかグラフに取ることができないのです。
なのでy-xグラフとy-tグラフの2種類のグラフがどうしても必要になってくるんですね。
つまり、この2つのグラフを両方使わないと波の情報をすべて得ることができないのです。
y-xグラフで読み取れること、y-tグラフで読み取れることには限りがあるので、グラフ問題を解くには必ず2つのグラフを用意するようにしてください。
では、2つのグラフの特徴と、そのグラフから読み取れることをまとめていきます。
y-tグラフ

まずはy-tグラフです。名前の通り、変位\(y\)と時間\(t\)のグラフです。
このグラフは\(x\)をある値に固定して考えて書かれたグラフになるわけです。
つまり、y-tグラフは
「ある位置\(x = x_0\)の点の動き」
を表すグラフなのです。

ある点が「\(t = 0\)でここ、\(t= 1\)でここ・・・」のように
波のある1点を時間的に追ったグラフなので、どう考えても波形を表すグラフではありませんね。
また、時間をちょっとずらした波形を書くのもできませんからね。
この辺りがごちゃごちゃになる人が多いので気をつけましょう。
y-tグラフから読み取れること

このグラフから読み取れることは2つです。
振幅\(A\)
周期\(T\)
速さが一番大きい位置
時間のグラフなので当然周期は求められて当然ですね。
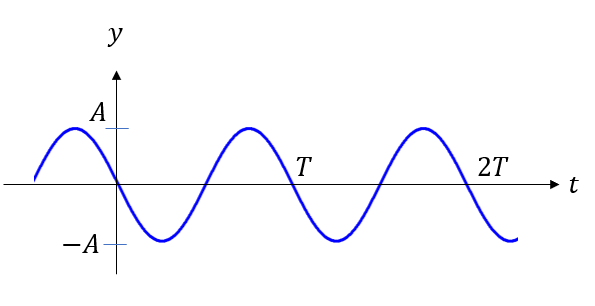
振幅\(A\)
振幅というのは波の山の高さ、あるいは谷の深さです。
今は\(x= x_0\)という点を取っていますが、正弦波であればどこの点をとっても振幅は同じです。
なので、このグラフで一番高くなるところ、あるいは一番低くなるところが振幅\(A\)となります。
周期\(T\)
周期は「ある点が1往復するまでにかかる時間」のことです(もしくは1波長が発生するまでの時間)。
つまり、このグラフで原点から始まって一往復した部分がちょうど周期\(T\)となりますね。
さらに、振動数も\(f= \frac{1}{T}\)を使えば求めることができますね。
速さが一番大きい位置
これはグラフ問題でよくあることですが、「一番振動の速いところはどこか?」「振動していない点はどこか?」というのが問われます。
振動の速さはy-tグラフの接線の傾きで測ることができます。
見ての通り、\(y=0\)となるときが一番速く、\(y = A,-A\)となるとき速さは0になりますね。
このように情報を読み取ることができます。
ここでは波長や波が伝達する速さは読み取ることができません。
y-xグラフ

y-xグラフは、文字通り、\(y\)と\(x\)の関係を表します。
このグラフ\(t\)を固定して書かれたグラフとなります。
つまり、
「\(t=t_0\)のときの波のそのもの」
を表します。

ある波を写真で取った感じですね。
これがまさに波形であり、
時間をちょっとずらしたときの波形を書く
というのも意味があるのです。
y-xグラフから読み取れること

y-xグラフから読み取れることはこれです。
振幅\(A\)
波長\(\lambda\)
各点の次の動き
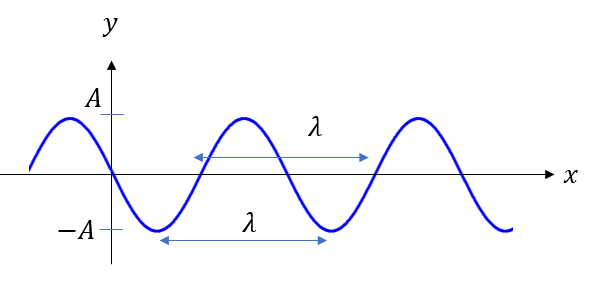
振幅\(A\)
これはy-tグラフの時と同じです。波の山(谷)の高さです。
波長\(\lambda\)
波長は「波一個分の長さ」のことです。波1個というのは上の図のような感じです。分かりやすいのは山から山、谷から谷ですね。
各点の次の動き
これは\(t = t_0\)という、ある瞬間の波を表したものです。なので、各点が次に上下どちらに動くのかが分かりにくくなっています。
そこで、ちょっとだけ時間を進めた波形を書くことで各点がどのように動くかがわかるようになります。

原点は上に動き、もう一方は下向きに動くのが図を見て分かりますね。
二つのグラフを使って読み取れること

この二つから
振幅\(A\)、周期\(T\)、振動数\(f\)、波長\(\lambda\)
を読み取ることができました。
これが分かることで、\(v = f\lambda\)より波の伝達速さも求めることができます。
\(v\)に関しては、問題文で与えられない限り、2つのグラフを使って導くしかありません。
問題ではどのように問われるのか?

最後に問題ではどのようなことが聞かれるのか教えます。と言ってもここまで見てきた通り、そこまで難しくないですよね?
各グラフが与えられて「周期を求めよ」「波長を求めよ」というのがまず問われます。
そして、グラフから「正弦波の式を求めよ」と問われることもあります。
また、y-tグラフを与えられたうえで「y-xグラフを描け」と問われることもあります(この逆もあり)。
ですが、どの場合も
「振幅\(A\)、周期\(T\)、波長\(\lambda\)、速さ\(v\)を求める問題」
にまとめることができます。
なので、グラフ問題が来たら、
必ずy-t, y-xグラフの2つを書き
振幅\(A\)、周期\(T\)、波長\(\lambda\)、速さ\(v\)の4つの物理量を求めるようにしてください。
まとめ

いかがでしたか?
波のグラフは分かってしまえば何も難しくありません。
グラフを何となくの理解でやるから、問題が解けないのです。
根本的なところをしっかり押さえたうえで問題に取り組めばどんな問題でも解くことができます!!
波のグラフ
・y-tグラフ、y-xグラフの両方を書く
・振幅\(A\)、周期\(T\)、波長\(\lambda\)、速さ\(v\)を求める。