【永久保存版】大学受験物理を攻略しよう!力学公式まとめ

こんにちは。
このページは必ずブックマークをしてください。
受験を勝ち抜くにはこのページは必須です。
ここでは
受験で忙しいあなたのために
物理に時間をかけたくないあなたのために
物理が大の苦手なあなたのために
力学の公式をまとめています!!
力学公式をただ覚えるだけじゃなく、意味そして問題での使い方を実際にお見せします。必ずすべて読んでください!!
目次
運動方程式
運動方程式はこういうものです。
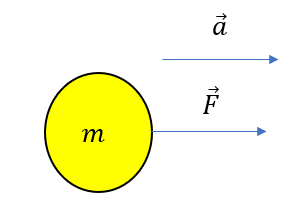
\(m\vec{a} = \vec{F}\)
運動方程式の意味って?
じゃあ、運動方程式の意味ってどういうことかというと上の文章の太文字がポイントです。(ほぼ全部ですが)
・ある一つの物体について成り立つ式である
→複数物体がある場合はそれぞれで立てる必要があり、どの物体にどんな力が働いているのかを見極める必要がある(力探し)
・ベクトルの関係式である
→実際に計算する際は軸を取り、それに合わせてプラスマイナスを定める必要がある
・加速度と合力は同一直線上にある
→分解してでも加速度と合力の方向は合わせる必要がある
・\(\vec{F}\)は合力である
→すべての力を考えないといけない(一つでも抜いたらアウト)
・質量、加速度、力の要素がある
→これらの要素がある(あるいはどれか一つを求める)なら使うべし
・物理のすべての公式は運動方程式から導出できる
運動方程式の使い方
じゃあ、運動方程式の使い方はどうするか?
ズバリこんな感じです。
使う場面
・加速度を求めたいとき(基本的に力と質量は問題で与えられます)
→「加速度を求めなさい」というものだけでなく、計算過程で加速度を求めなければならない場合も必要になってきます。
・単振動や円運動の問題を解く時
→教科書や問題集では円運動や単振動に関して公式的なものが載っていますが基本的に運動方程式から本番も解きます。
↓運動方程式の使い方↓

例題
次の二つの物体それぞれの加速度の大きさを求めなさい
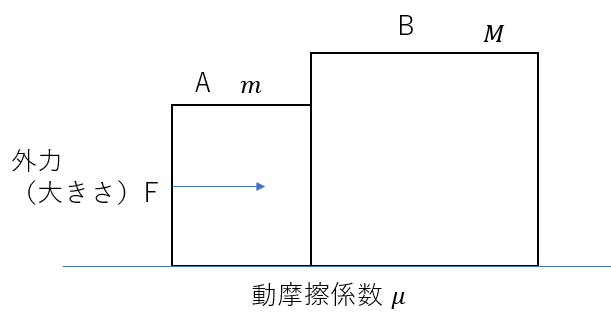
(解答)
まず、力の情報があって「加速度を求めよ」なので間違いなく運動方程式を使います。
あとは手順通りにやっていきます。
1.注目する物体を決める
まず、注目する物体を決めます。注目する物体は原則1個です。Aと決めたらAだけについて考える。Bと決めたらBだけについて考える。という感じです。
まずAについて考えます。
2.軸を取る
次に軸を取ります。軸というのは「正方向を決める」ということです。力や加速度などのいわゆるベクトル呼ばれる、向きをもったものは必ずどの向きを正にするかを決める必要があります。
軸の決め方のポイント
物体が動き出す(と思われる)向きを正に取る
今回は右向きに動き出すと考えられるので右向きに軸を取ります。(これ以降勝手に軸を変えてはいけません)
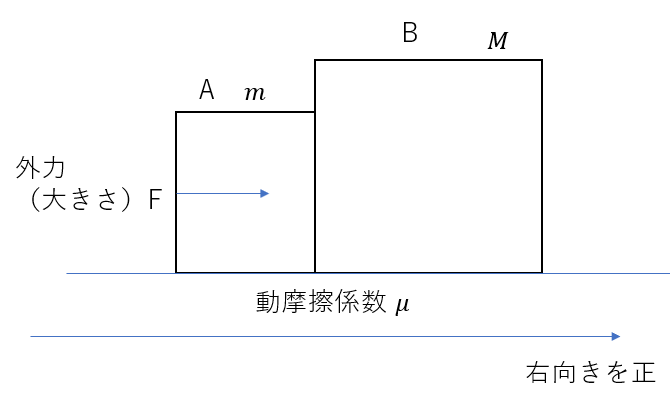
3.力を書きだす
次に力を書きだします。何度も言いますが、1で注目した物体が受ける力だけを書きます。
力は絶対に過不足なく書きださないといけません。ここを何となくやる人がいますがそれは自殺行為だということは理解しておいてください。
力探しのポイント
・まず遠隔力(重力や静電気力)を書く
・物体を一周して接触している部分の力を書く
このようにすれば絶対にミスはありえません。
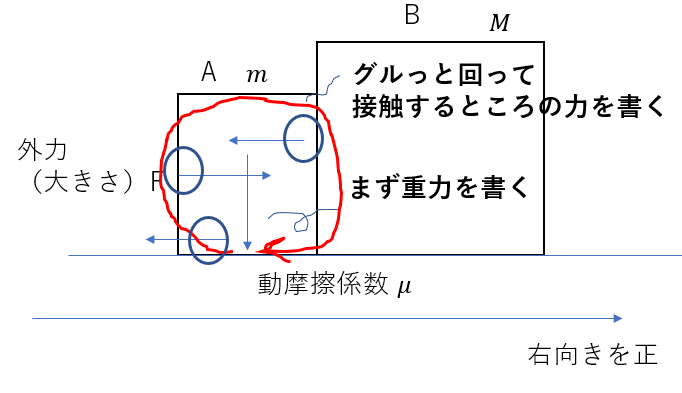
(垂直抗力は図が汚くなるので書いていません)
それぞれの力の大きさは
重力:\(mg\)
動摩擦力:\(\mu mg\)
外力:\(F\)
Bから受ける力:\(T\)(←自分でおいたもの)
4.合力を求める
次に合力を求めます。今回の場合、軸を右向きに取ったので、同じ向きならプラス、逆向きならマイナスを、先ほど求めた力に付けて足していきます。
合力\(F_s = -\mu mg + F – T\)
5. 運動方程式を適用
あとは運動方程式を立てるだけです。
\(ma = -\mu mg + F – T\)
これでAに関してはOKです。
同じ事をBについてやっていきます(自力でやってみてください)
注意!
1のステップをおろそかにしていると。。。
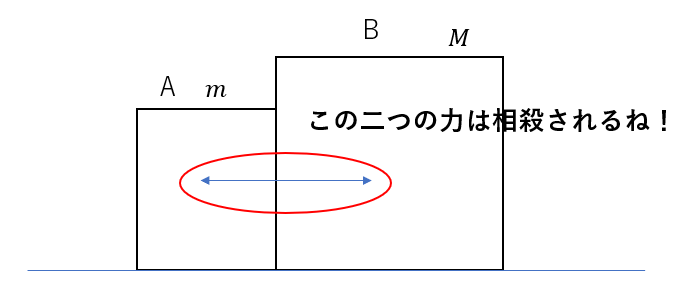
このような勘違いが起こりやすくなる。
→これらはAが受ける力とBが受ける力、つまり受けている物体がそもそも違うので相殺もくそもありません!
・2のステップをおろそかにしていると・・・
単振動で混乱します!!
→今のうちのこういうクセをつけておきましょう。
等加速度運動の公式
加速度が一定のとき
\(\vec{x} = \vec{v_0}t + \frac{1}{2}\vec{a}t^2\)
\(\vec{v} = \vec{v_0} + \vec{a}t\)
\(v^2 – v_0^2 = 2\vec{a}\vec{x}\)
*\(\vec{x}\)などの記号はプラスマイナスを考慮する必要があります。
一応導出はできますが、いちいち導出するのは面倒なので覚えちゃいましょう。
(一番上の式だけ覚えていればtで微分することで真ん中の式になりますし、二つの式を使えば一番下の式も出せます。)
等加速度運動の公式の意味
・加速度一定の場合にのみ適用できる
→加速度一定じゃないときは使えません!!
・ベクトルの式である
→軸を取ってプラスマイナスを考える必要がある
・\(\vec{x}\)は変位である
→(あとの位置 - 前の位置)となります
・時間の情報があって、変位や速さを求めるときに使う
→運動方程式などで加速度を出して、この公式に使うことが多いです。
・時間を求める場合にも使う
使い方
基本は運動方程式と同じです。
1. 軸を取る
2. 求めたいものが含まれる式を適用
例題
図のような物体の運動を考える。斜面を下り切ったときの速さを求めよ
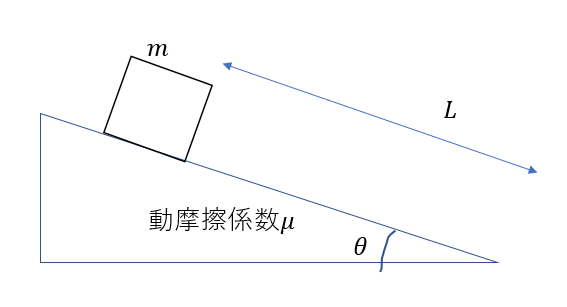
早大生はこう考える!
まず、今回の問いは速さを求めます。等加速度運動の公式を使うかな?となりますね。しかし、公式を使うには加速度と時間の情報がありません。
時間の情報は、距離が分かっているので公式1を使えばわかるので、加速度さえ情報として手に入ればOKです。
加速度を知りたい・・・はい!当然、運動方程式ですね。
まずは運動方程式を使って加速度を求めます。
解き方は省略しますが、先ほどの通りに運動方程式を立てて導いてください。
(ポイントは軸の取り方。今回斜面を滑り下りるので斜面に沿った軸を取るといいでしょう。)
求めると
\(a = g\sin{\theta} – \mu g \cos{\theta}\)
加速度が求まったので時間を求めます。
見ての通り\(a = 一定\)ですよね。\(g, \mu, \theta\)はすべて一定ですから。
なので等加速度運動の公式が使えます。
まず時間を求めたいので1つめの式を使います。(変位が含まれている式)
等加速度運動の公式を使うので軸を取ります。等加速度運動の公式はベクトルの式ですので、プラスマイナスを考慮しないといけません。ですから正の向きを定めるのです。
軸の取り方は原則物体が動きだす向きです。今回は斜面下向きがいいでしょう。
(もちろん水平にも取れますが、その場合鉛直方向に関しても式を立てないといけないのでかなり面倒です)
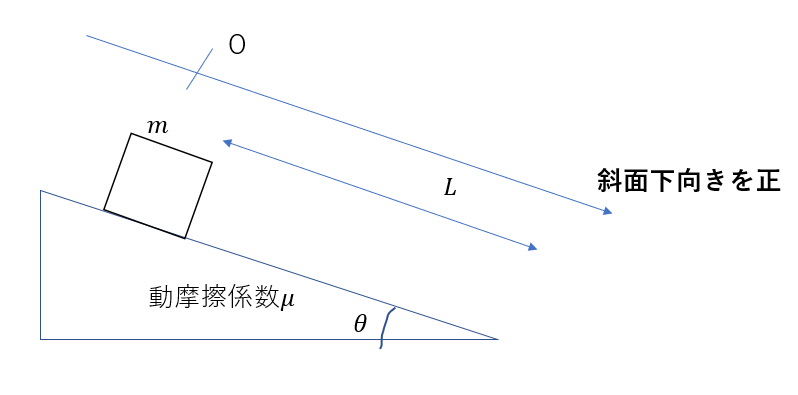
*今回原点を取っています。その理由はこの次分かります。
そして等加速度運動の公式
\(\vec{x} = \vec{v_0} t + \frac{1}{2}\vec{a}t^2\)を使います。
プラスマイナスを判断しないといけませんが。
加速度は見ての通りプラスです。
変位は「後-前」をやればOKです。つまり\( L – 0 = L\)です。
(軸を逆向きに取ったらLが-Lに変わります)
このように出発点を原点に取っておくと変位の計算が楽になるので、今回は原点を分かりやすく設定しました。
あとは当てはめばOKです。
\(t = \sqrt{\frac{2L}{a}}\)(ここでは\(a\)のままにしておきます。)
あとは2つ目の式を使っておしまいです。
\(v = \sqrt{2aL} = \sqrt{2L(g\sin{\theta} – \mu g \cos{\theta}}\)
仕事とエネルギー
エネルギー原理とエネルギー保存則
・エネルギー原理
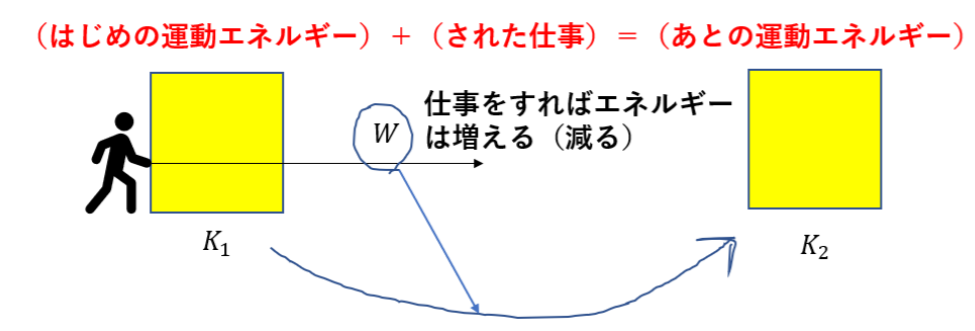
・エネルギー保存則
*エネルギー原理が根本にあり、そこから導けるのが力学的エネルギー保存則です。
2物体が内力を及ぼすとき
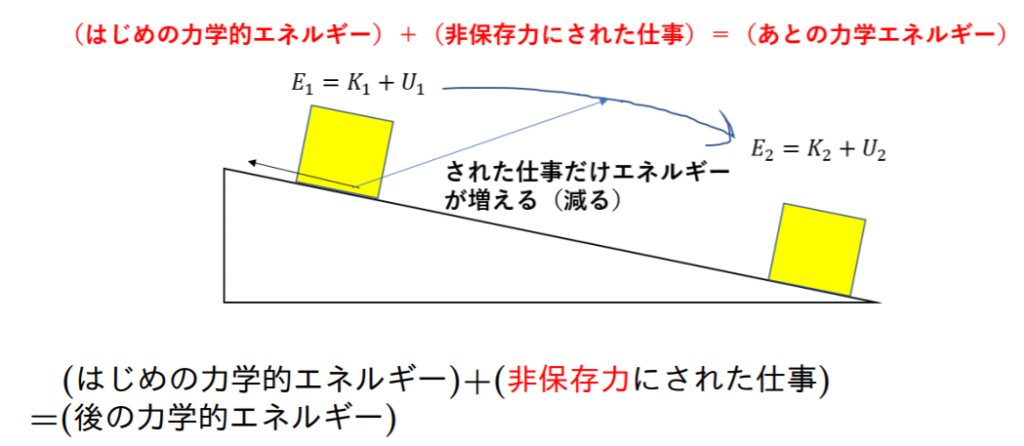
(初めの力学的エネルギーの和)+(外力にされた仕事)=(あとの力学的エネルギー)
→内力による仕事は片方がプラス、片方がマイナスになるので打ち消しあうというイメージ
イメージは「仕事をされればエネルギーが増える」です。
公式の意味とは?
エネルギー原理
・運動エネルギーとすべての仕事の関係である
→特に仕事は重力でもばねでも摩擦力でもされた仕事はすべて含まれる(力学的エネルギー保存則と混ざらないように)
・仕事には正と負の仕事がある
エネルギー保存則
・力学的エネルギーと非保存力にされた仕事の関係
→エネルギー保存則と混ざらないように
どちらにも言えること
・時間が分からない、加速度が一定じゃないときに速さなどを求めるときに使う
→等加速度運動の公式が使えないときの対処
・力が一定じゃなくて、仕事をダイレクトに求められないときに使う
→仕事は基本的に力が一定じゃないと求められないのでその対処法
・「最大の速さ」や「最高点」などで使える
→運動エネルギー=0、位置エネルギー=0となる状況を考えることが多い
・最初と最後の状態が分かっているときに使える
使い方
例題
図のように質量\(M\)と物体Aと質量\(m\)の物体Bを軽い糸でつなげる(\(M > m\))。Aが坂の上を距離\(l\)だけ滑り下りたときを考える。ただし、斜面とAの動摩擦係数を\(\mu’\)とする。
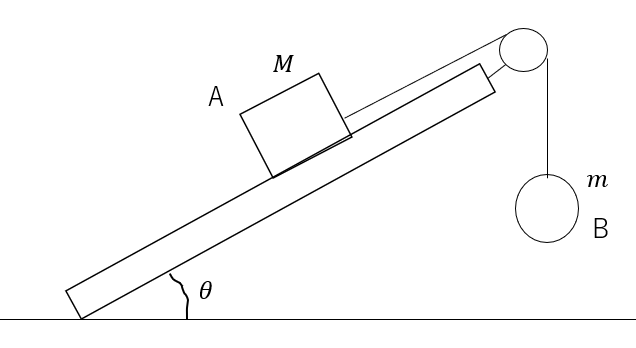
(1)Aの速さを求めよ
(2)Aの力学的エネルギーの変化量は正、負、0のいずれか。
早大生はこう考える
速さを求めたいから等加速度運動の公式が使えるかな・・・と思ったけどこれって計算面倒!それぞれの運動方程式を立てる必要があるし、等加速度運動の公式も使わないといけないし。だったら、エネルギー保存則で一発で行こう!
(2)でもエネルギーの話が出てきているから繋がりそうだからね。
解答
エネルギー原理でもエネルギー保存則でもどっちでも解けますが、まあ力学的エネルギー保存則の方が良いですね。
ポイントとなるのは非保存力にされた仕事です。これを求めていきましょう。
まずAから
今回の非保存力は、摩擦力と糸の張力
どちらも一定の力なので仕事は「力×距離」で表すことができます。
動摩擦力の仕事:\(-\mu’ Mg \cos{\theta} \times l\)
張力にされた仕事:\( – Tl\)
また力学的エネルギーはそれぞれ
始め:\(Mgl\sin{\theta}\)
終わり:\(\frac{1}{2}Mv^2\)
なので、Aに関してエネルギー保存則を立てると(位置エネルギーの基準はすべり下りたところ)
\(Mgl \sin{\theta} – \mu’ Mg\cos{\theta} \times l – Tl = \frac{1}{2}Mv^2\)
同様にBについても考えます
張力にされた仕事:\(Tl\)
始めの力学的エネルギー:\(0\)
あとの力学的エネルギー:\(\frac{1}{2}mv^2 + mgl\)
(位置エネルギーの基準点は最初の位置)
あとはエネルギー保存則を適用して
\(0 + Tl = \frac{1}{2}mv^2 + mgl\)
AとBでそれぞれ出した式は足したくなりますよね?Tは自分で置いたものなので消去しないといけませんが、足すことで解決します。
\(Mgl\sin{\theta} – \mu’ Mg \cos{\theta} \times l = \frac{1}{2}Mv^2 + \frac{1}{2}mv^2 + mgl\)
この式はまさに最初に紹介した2物体のときのエネルギー保存則になりますね。張力が内力に当たります。
\(v = \sqrt{\frac{2(M(\sin{\theta} – \mu’ \cos{\theta}) – m)gl}{M + m}}\)
となりますね
(2)
これはAについてのエネルギー保存則を見ればOKです。
(初めの力学的エネルギー)+(非保存力にされた仕事)=(あとの力学的エネルギー)
なので、左辺の(初めの力学的エネルギー)を右辺にもっていけば
「後ー前」となり、力学的エネルギーの変化量がでます。
非保存力にされた仕事は見ての通りマイナスだったので負になりますね
運動量
物体が一つ
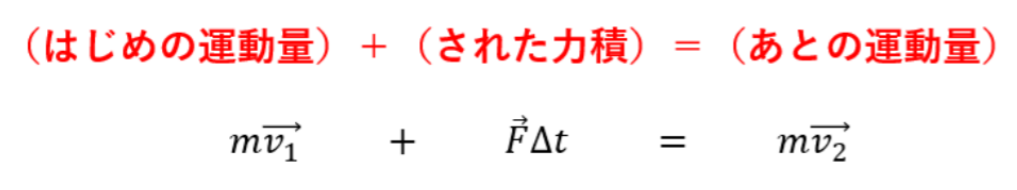
上の式の拡張
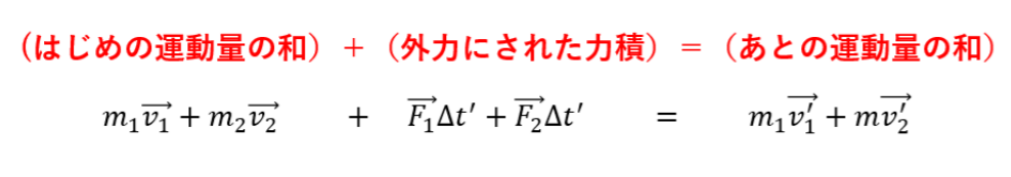
反発係数
\(e = – \frac{v_1 – v_2}{v_1′ – v_2′}\)
(\(e = -\frac{衝突後の相対速さ}{衝突前の相対速さ}\))
*仕事とエネルギーの関係とそっくり!!
運動量保存の意味とは?
・ベクトルの関係式
→軸を取ってプラスマイナスを考慮する必要がある
・外力にされた力積である
→内力のみだったら0=教科書に載っている運動量保存則
・複数の物体が出てくるときに有効
→物体同士で及ぼしあう場合は運動量保存が力を発揮
・重心や二体問題で効果を発揮
→抜群に相性がいい
・反発係数とセットで使う
入試で使う公式TOP3に入りますね。
使い方
図のように質量\(m\)の小球と、質量\(M\)の台がある(\(m < M\))。台には曲面ABがありB付近は水平になっていて、壁Wがある。Bから高さ\(h\)のA地点に小球を置き静かに放すと、小球はWと弾性衝突した。ただし、台は固定されておらず、すべての面で摩擦はないとする。
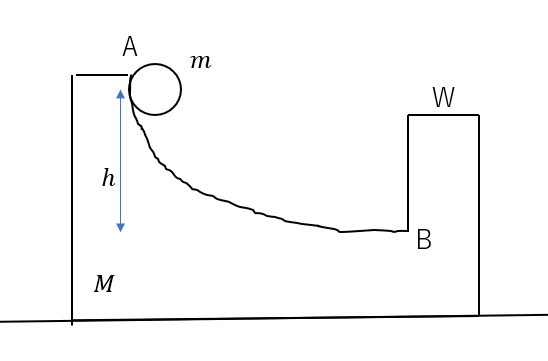
(1)Wに衝突する直前の小球と台の速さをそれぞれ求めよ
(2)Wに衝突後小球が到達する最高点の高さを求めよ
(河合塾「名門の森」 問題17)
早大生はこう考える
(1)速さを求めたいから、使えそうなのは速さを式に含んでいる運動量保存やエネルギー保存則だな。運動量保存なら外力は働かないからうまくいきそうだし、非保存力もないからエネルギー保存則もうまくいきそうだ。台は固定されていないから注意だね
(2)まず衝突だから反発係数が関係しそうだな。最高点がヒントだね。台も小球も動くから最高点っていうのは・・・同じ速さになったときだな(相対速度が0になったときだな)
解答
(1)
速さを求めたいので、速さを含んだ式を使うこと。運動量保存やエネルギー保存が今回は役に立ちそうです。
まずは運動量保存を適用します。
今回水平方向には外力は働きません。
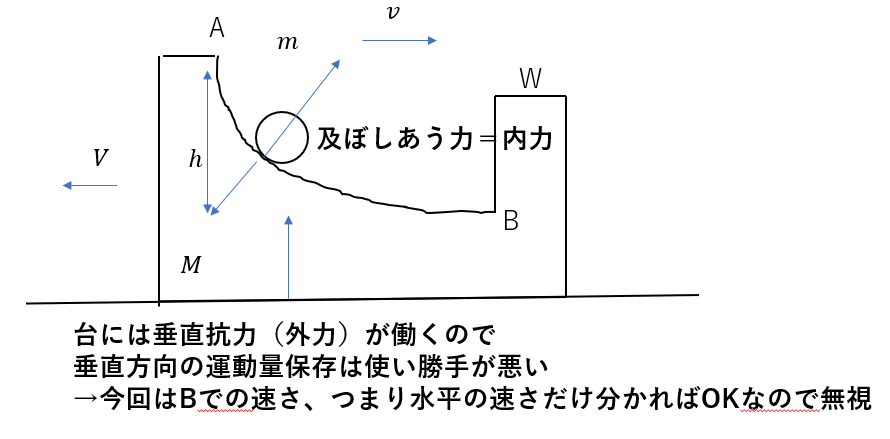
小球と台の速さをそれぞれ\(v, V\)とすると
(初めの運動量の和)+(外力にされた力積)=(あとの運動量の和)
ということで(軸は右向きを正)
\(0 + 0 = mv – Mv\)
よって\(MV = mv\)
となります。
向きが明らかな場合は速さを考えることで計算が楽になります。
もし、速度で考えるとしたら、必ず軸の向きに合わせて速度を取ります。この場合
\(0 = M\vec{V} + m\vec{v}\)
\(-M\vec{V} = m\vec{v}\)
となります。
これの意味は「小球と台の速度の向きは逆」ということが分かるので
\(\vec{v}をv\)に、\(\vec{V}を-V\)に置き換えることで、結局同じ計算結果になります。
次にエネルギー保存則ですね。
今回はダイレクトに、2物体のエネルギー保存則を使ってみましょう。
すると、外力のする仕事は0になりますから非常にきれいな式になります。
初めの力学的エネルギーの和:\(mgh\)
外力による仕事:0
後の力学的エネルギーの和:\(\frac{1}{2}mv^2 + \frac{1}{2}MV^2\)
ということで
\(mgh = \frac{1}{2}mv^2 + \frac{1}{2}MV^2\)
ということになりますね。
注意
実は今回の問いは小球、台をそれぞれ別々でエネルギー保存則を立てると解けません。正確には、解けるんですがどえらい時間がかかります。小球がされる仕事と台がされる仕事が打ち消しあうことを示さないといけないからです。
なので、ダイレクトに「2物体の場合のエネルギー保存則」を使うのが良い場合もあります。ちなみに内力同士が及ぼす仕事は相殺されることは証明できるので、気になる人は調べたりしてみてもいいかもしれません。
後は、二つの式を使って求めればOKです。
\(v = \sqrt{\frac{2Mgh}{M + m}}\)
\(V = \frac{m}{M}\sqrt{\frac{2Mgh}{M + m}}\)
(2)
二物体で最高点ときたら、両者が同じ速度(相対速度が0)という条件を思い浮かべてください。
ですが、今回の場合、速度の向きが逆向きなので速度が同じになるには両者の速度が0になるしかありません。
衝突まで外力のした仕事は0、つまり力学的エネルギーは保存されています。衝突後も同じです。
さらに弾性衝突するのでエネルギーは失われません。
力学的エネルギーが保存されるなら、行って帰ることが可能になります。
つまり・・・はい、元の状態に戻るんですよ。
ということで最高点は\(h\)となります。
円運動
速さ:\(v = r\omega\)
加速度の大きさ:\(a = r\omega^2 = \frac{v^2}{r}\)
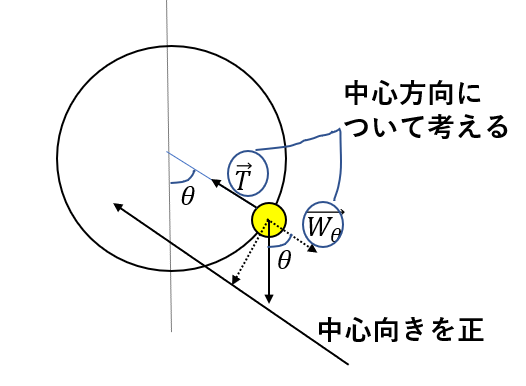
円運動ときたらやることはたった二つ!
・中心方向の運動を立てる
・エネルギー保存則を使う
こんな条件は要チェック
・「物体が一周する」
→常に中心向きの合力が働く
・「糸がたるむ」「床から離れる」
→張力(垂直抗力)が0
・途中で糸を切り離した
→等加速度運動になる
使い方
単振動
・\(F = – (定数) \times (xの一次式)\)
→これが単振動の条件
・単振動の加速度:\(\vec{a} = -\omega^2 \vec{x}\)
→ベクトルなのでもちろん、軸を取ってプラスマイナスを考慮する必要があります。
・周期\(T\)と角振動数\(\omega\)の関係:\(T = \frac{2\pi}{\omega}\)
・単振動の最大の速さ:\(v = A\omega\)(A:振幅)
・単振動のエネルギー
\(a = -(定数) \times (xの一次式)\)について
・定数→ばね定数
・中心→ばねの自然長
の一つのばねとみなせる
すべては運動方程式を確実に使いこなすことができるか?これが一番重要です。(単振動の問題の解き方を見た方が早いです)
単振動の解き方
基本はこれ。

そうです。運動方程式を立てていきます。
そして、その中で上の単振動の条件を満たした場合に単振動だと分かるわけですが、その時に必ずやってほしいことがあります。
1.振動の中心を求める
→\(a = 0\)のときの位置\(x\)
2.\(a = -\omega^2 (x – x_0\)として\(\omega\)を求める
→\(\omega = \sqrt{定数}\)
3.周期\(T\)を求める
→\(T = \frac{2\pi}{\omega}\)
ばね定数\(k\)の軽いばねを滑らかな水平面上に置き、その右端に質量\(m\)の物体Aを取り付ける。また質量\(3m\)の物体BをAに接するように置く。自然長自のAの位置を原点に取り、そこから長さ\(d\)だけ縮めた後に静かに放す。
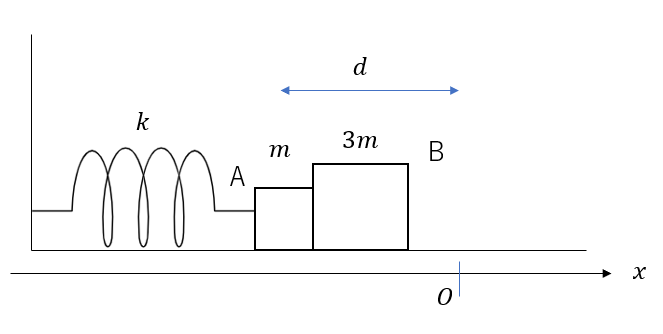
(1)しばらくの間AとBは一体に運動する。この時のAがBを押す力の大きさ\(N\)を求めよ
(2)AとBが離れるときの位置\(x\)とBの速さ\(u\)を求めよ
(3)動き始めてからAとBが離れるまでの時間\(t_0\)を求めよ。
(河合塾 「名門の森」 問題32)
早大生はこう考える!!
(1)(2)(3)どれも単振動の一連の流れをやればすべて行けそうだな。(3)は周期が使えそうだからなおさら一連の流れ(周期を求めるところまで)やるべきだね。(2)は離れるってことは・・・AがBに与える力が無くなるときだね。(1)と繋がりそうだ!
解答
この問題はどう見ても単振動ですね。実は単振動ってやること決まっています。今回はその典型で上でまとめたステップ(周期を求めるところまで)を踏めば解ける問題になっています。
(1)
まずは普通に運動方程式を立てましょう。
Aについてみていきます。軸はすでに取ってあるので問題に従いましょう。
ちなみに問題に書いてなくても軸は取りますが、単振動のときは原点を必ず決めてください!原点の取り方は自然長の位置です。
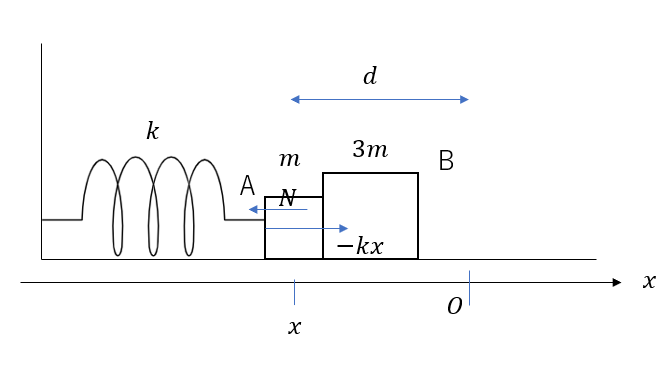
そして力探しをしていきますが、位置\(x\)にあるAについて
今回は二つの力を受けています。(重力などは関係ないので無視しています)
Bから受ける力(大きさ\(N\))
ばねの弾性力(大きさ\(kx\))
ここまでは良いですね。
これらは力ですから、プラスマイナスを考慮する必要があります。
Bから受ける力は明らかに逆向きなので\(-N\)となります。
問題はばねの弾性力です。
軸と同じ向きを向いていますから一見\(kx\)のままで良さそうですが・・・
これは間違いです。
この\(x\)は図を見てわかるように負の値ですよね。つまり、力をプラスにするにはマイナスをつける必要があります。
つまり\(-kx\)となるわけです。
後は合力を求めて運動方程式を適用するだけです。
\(ma = -kx – N\)
同じようにBについても考えます。が、簡単ですね。
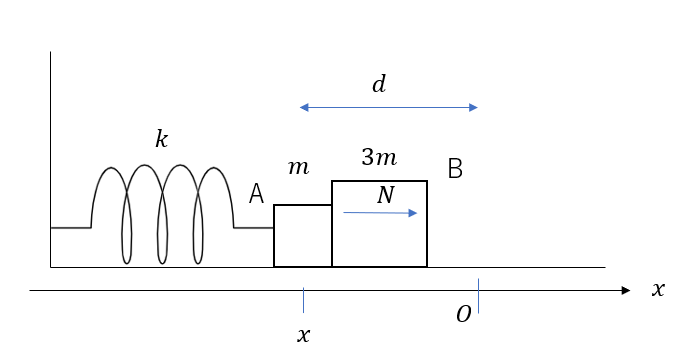
Aから受ける力(大きさ\(N\))しか受けていませんね。
\(3ma = N\)
後は二つの式から\(a\)を消せば終わりです。
\(N = -\frac{3}{4}kx\)
(2)
A,Bが離れるということは二つが及ぼしあう力が0になること。つまり\(N = 0\)です。
(1)の答えを使えば\(x = 0\)ですね。ここが離れる位置です。
また速さですが、等加速度運動の公式、運動量、エネルギー保存則がなどが使えそうですが、今回は出発点と最終店の状態が分かっていますね。単振動なので等加速度でもないです。
ということでエネルギー保存則ですね。非保存力にされた仕事もゼロなので使い勝手がいいでしょう。今回は例の2物体のエネルギー保存則です。
・初めの力学的エネルギーの和:\(\frac{1}{2}kd^2\)
・外力にされた仕事:0
・後の力学的エネルギーの和:\(\frac{1}{2}(m + 3m)u^2\)
ということで、
\(\frac{1}{2}kd^2 + 0 = \frac{1}{2}(m + 3m)u^2\)
\(u = \frac{d}{2}\sqrt{\frac{k}{m}}\)
となります。
(3)
A,Bが離れるまでは単振動していますから周期を使えば時間が出せそうですね。まあ、単振動なので普通にそこまで導くのが良いのですが。。。
(1)で求めた運動方程式の両辺を足すと
\(4ma = -kx\)
\(a = -\frac{k}{4m} x\)
これは単振動の条件の形をしていますね。やはり単振動するということが確認できました。次に3つのステップをやっていきます。
1.中心を求める
これは\(a = 0\)の\(x\)を求めるということです。今回は明らかですが\(x_0 = 0\)が中心です。
2.\(a = -\omega^2 (x – x_0)\)として\(\omega\)を求める。
単振動の加速度は\(\vec{a} = -\omega^2 \vec{x}\)というのが分かっているのでこれを利用しているだけです。
ちなみにこれを計算すると\(\omega = \sqrt{定数}\)と必ずなるので、ダイレクトに求めてもOKです。
\(\omega = \sqrt{\frac{k}{4m}}\)
3.周期を求める
後は周期です
\(T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{4m}{k}}\)
そして今回求める\(t_0\)って端から中心に着くまでですから、周期の4分の1ですよね。
ということで
\(t_0 = \frac{1}{4} T = \pi \sqrt{\frac{m}{k}}\)
となるわけです。
まだまだ不十分です
というわけで力学の公式集はこれにて終了です。
なんかイケそうじゃありませんか?
ちなみに、問題は「名門の森」から出しているものが多いです。でも、そんなに難しく感じなかったのでは?と思います。
このページは定期的に更新していく予定です。何度も見直してください。
ただ、これはまだまだ教えていないことが多くあります。
重心を使った単振動(二体問題)などの解説は公式集では教えていません。
また、これはあくまで一気にまとめて理解をしているだけで、不安定な状態です。
なので、もっと詳しく。そして、もっとしっかり土台を作りたいというあなたはぜひこちらの教材を使ってみてください









