電磁誘導のマイナスって何よ!困らない起電力の向きの求め方。

電磁誘導の式って\(V = -N\frac{\Delta \Phi}{\Delta t}\)じゃないですか。この「マイナス」の意味が分からないんですが。
 AI
AI
分かった。今日はなんで電磁誘導でマイナスが付くのか?っていうところを解決しよう。
 AKINORI
AKINORI
ファラデーの電磁誘導の法則。
ありますよね。
電磁誘導による起電力は
\(V = -N\frac{\Delta \Phi}{\Delta t}\)
と書けます。
ここで、このマイナスの意味が分からない!!っていう人が多発します。
これについて説明したいと思います。
閉回路に磁束が貫くと・・・
そもそも電磁誘導っていうのを説明しないと、このマイナスの意味を教えられないので、まずは電磁誘導の説明から。
コイルに磁石を近づけたり遠ざけたりするとどうなるか知ってますか?
電流が流れる?
 AI
AI
そだね。中学校でやったと思う。
 AKINORI
AKINORI
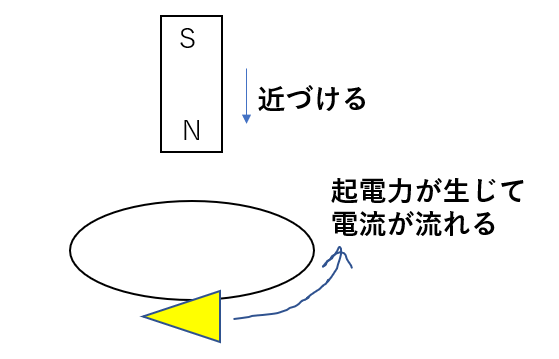
これのプロセスはこうなっています。
ポイントは
磁束の変化
と
コイルはツンデレ
です。
コイルはツンデレっていうのは後程わかります(笑)。
N極からは磁場(磁束密度)が出ていますね。
↓磁束密度についてはこちら↓
これが、コイルを貫きます。
貫く磁束密度をすべて合わせたものを磁束と言いましたね。
もっと言えば、
磁束は ”磁力線の総本数” という意味です。
N極を近づけることで、
磁力線の本数、つまり磁束が変化します。
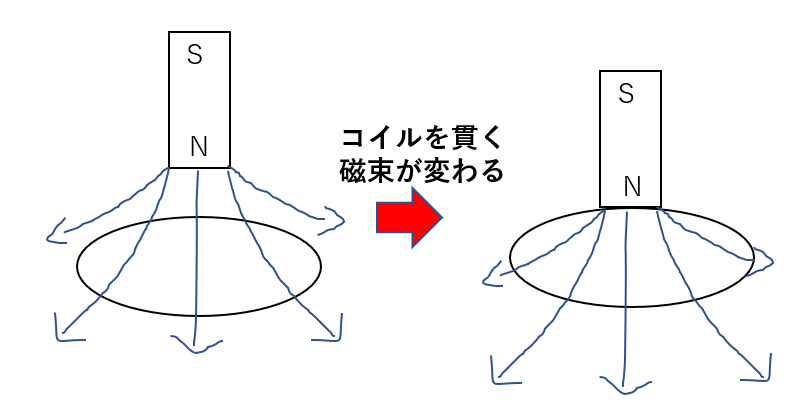
すると、コイルはこう思います。
「磁束来ちゃダメ~~!!」

ってことで、磁束が増えた分を帳消しにしようとします。
上向きに磁束を作ろうとするのです。
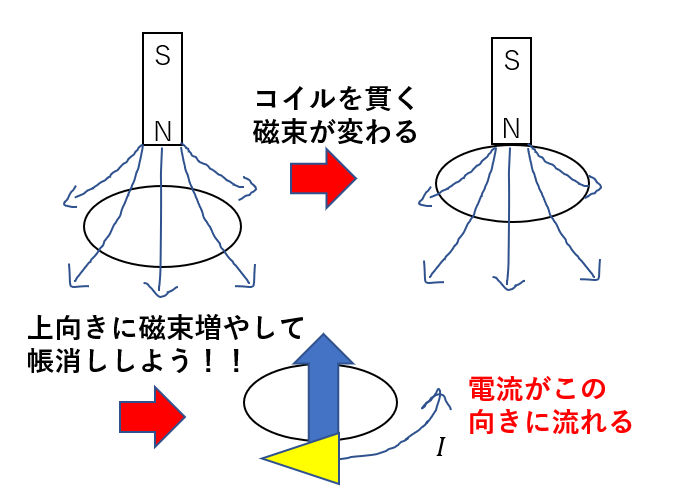
磁束(磁束密度)を作るには、電流を流さないといけませんね。
右ねじの法則を使えば、図のような向きに電流が流れることが分かります。
同じように、コイルを遠ざけると今度は磁束が減りますね。
そうするとコイルちゃんはこう思います。
「磁束行っちゃダメ~~!!」

ってことでやっぱり変化した分を取り戻そうとするわけですよ。
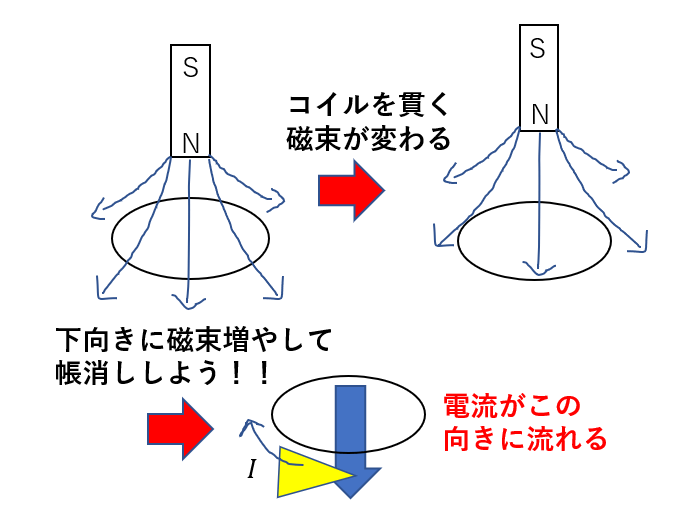
ということで、図のような電流が流れます。
このように、コイルは磁束が変化すると、その変化を戻そうと電流と起電力を生じる
これがレンツの法則と言われるものです。
見ての通り、
コイルはツンデレ
です。
磁束が変化すると
「別に来てほしいなんか言ってないんだからね!!」
「行っていいなんて一言も言ってないんだから!!」
って言うんですよ。
これがレンツの法則です。
これを元に起電力を式にしたのがファラデーさん
なるほど!これが電磁誘導が起こるプロセスってわけですか。
 AI
AI
そう。そして、じゃあ実際にどれだけの起電力が生じるの?っていうのを見つけたのがファラデーという人です。
 AKINORI
AKINORI
ファラデーさんは実験的に次の式を導いたわけです。
起電力の向きを無視すると
\(V = N\frac{\Delta \Phi}{\Delta t}\)
と表せます。
イメージで言うと。
\(\frac{\Delta \Phi}{\Delta t}\)
はどれだけ磁束が変化するかです。
変化が多いとコイルはよりツンデレ度を増します。ですから、起電力も大きくなります。
また\(N\)はコイルの巻き数ですが、
コイルの巻き数を増やせばツンデレの人数が増えるので、やっぱり起電力も大きくなります。
ですから、この式は納得いきますね。
そして、マイナスなんですが、
結論を言うと
マイナスは無視してもOK!!
です。
じゃあ、教科書に載ってるマイナスって何!?
 AI
AI
あれは、起電力を向きの決め方が影響しているんだ。
 AKINORI
AKINORI
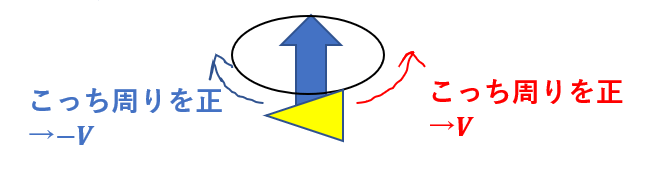
例えば、この場合、
赤の周りを正にしたら同じ向きなので\(V\)
青の向きを正にしたら逆向きなので\(-V\)
ベクトルと同じ考え方です。
教科書では一般的な式にしたいので、
磁束を貫く向きを基準
にして考えます。
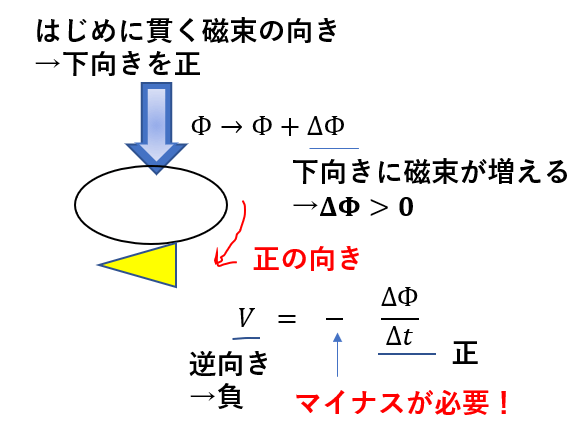
最初の磁束の向きは下向きなので、これを基準にしたとき、
その周りをまわる電流などの正向きは右ねじの法則にしたがいます。
この場合、図のような向きを正に取るわけです。
この時、起電力は逆向きなので、\(V < 0\)とならないといけません。
下向きに磁束が増えると\(\Delta \Phi > 0\)ですので、マイナスをつける必要があるわけです。
下向きの磁束が減る場合も同じです。
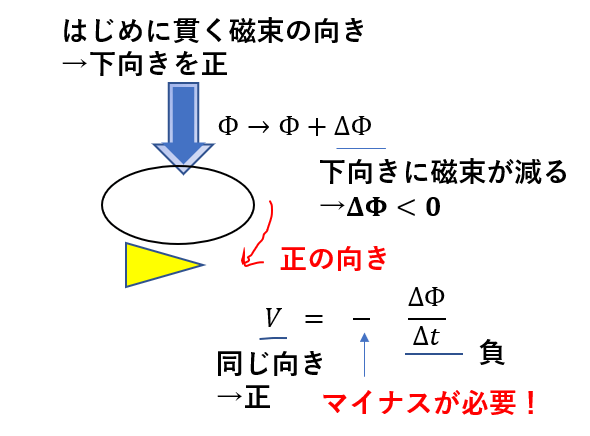
今度は同じ向きを向くので\(V > 0\)となるんですが、
\(\Delta \Phi < 0\)となって、結局マイナスが必要になります。
このように、一般的に式を出そうとすると
\(V = -N\frac{\Delta \Phi}{\Delta t}\)
という風にマイナスが出てくるんですね。
なるほど!
 AI
AI
実際に問題を解く時は?
こうやって一般的な話にすると結構混乱します。
なので、問題を解く時は
- まず起電力を求める
- レンツの法則で実際の向きを決める
このステップを踏んで解けばOKです。
まとめ
いかがでしたか?
ファラデーの電磁誘導の式のマイナスは向きを決めたいからつけたものだったんですね。ですから、あまり気にしなくていいです。
まずは大きさ。そして向き。
この流れをしっかり踏んでいきましょう!
ファラデーの電磁誘導の法則
\(V = -N\frac{\Delta \Phi}{\Delta t}\)
実際に問題を解く時
- 大きさを求めて
- 向きを決める
この手順でやる!!
電磁誘導の問題演習はこちらで!