コンデンサーのリアクタンスって何よ!交流回路のコンデンサーを理解する

・コンデンサーの位相変化についてわかる
・コンデンサーのリアクタンスについてわかる
こんにちは。今回は交流回路のコンデンサーについてみていきます。
コンデンサーの電流が電圧よりなんで\(\frac{\pi}{2}\)進むの?
コンデンサーのリアクタンスって何なの?
という疑問をここで解決していきます。
交流回路では抵抗、コンデンサー、コイルの3つの素子についてしっかり理解をし回路問題に臨んでください。
↓抵抗、コイルも確認しよう↓
交流回路におけるコンデンサー

交流回路では以下の二つの観点から性質をとらえていきます。
・電流と電圧の関係
・直流回路への変換
やることはコイル編と同じです。
図のような場合、コンデンサーの役割について考えていこう。
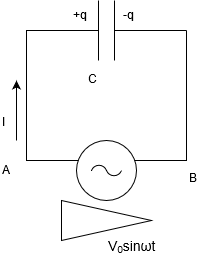
電流はどう表される?

まずは電流についてみていきます。
コンデンサーに\(q\)[C]の電荷が蓄えられたとき、\(Q = CV\)より
\(q = CV = CV_0\sin{\omega t}\)
コンデンサーに流れる電流\(I\)は電流の定義式から
\(I = \frac{\Delta q}{\Delta t} = CV_0 \frac{\Delta \sin{\omega t}}{\Delta t}\)
時間は限りなく小さくとらないといけないので\(\Delta t \to 0\)
すると
\(I = CV_0 \frac{d}{dt}\sin{\omega t}\)
まさに微分!!ですね
\(\sin{\omega t}\)を\(t\)で微分しろということです。数Ⅲをやっているあなたならできますね。
\(I = \omega C V_0\cos{\omega t}\)
もちろんこのままでいいんですが、この次の説明のために変形します。
\(sin{(\omega t + \frac{\pi}{2})} = \cos{\omega t}\)を使って
\(I = \omega CV_0 \sin{\omega t + \frac{\pi}{2}}\)
と表すことができます。
電流と電圧の位相差は?

電流の式は出ましたが、もう少し見ていきます。電圧と電流の式を見比べてみます。
\(V = V_0\sin{\omega t}\)
\(I = \omega CV_0\sin{\omega t + \frac{\pi}{2}}\)
注目すべきはsinの中。sinやcosの中は位相を表します。
位相というのは、簡単に言うと変化の仕方のことです。電圧が最大値(最小値)を取るとき、電流も最大値(最小値)を取るなら位相が同じで、撮らない場合は位相がずれているとなります。
電圧の\(\omega t\)に対し、電流は\(\frac{\pi}{2}\)だけ足された形になっていますね。つまり、
電流は電圧より\(\frac{\pi}{2}\)だけ位相が進んでいる
ということが分かります。位相が違うということなので、電圧が最大値を取ったときに電流は最大値を取っていないということになるわけです。
電流の方が電圧の前を走っているって感じですね。
とまあ、大事なのは「電流が電圧より\(\frac{\pi}{2}\)だけ位相が進んでいる」というところが大事で、あまり位相に関して深く考えない方が良いです。
コンデンサーのリアクタンス

次に「交流を直流とみなす」ことについて考えます。交流を直流にみなすってことは実効値を使うということです。
↓実効値に関してはこちら↓
実効値は最大値と大きく関係しているので最大値について考えます。
さっき導いた電流の式から、電流の最大値は
\(I_0 = \omega C V_0\)です。つまり、
\(V_0 = \frac{1}{\omega C} I_0\)
実効値は「最大値に\(\frac{1}{\sqrt{2}}\)倍」なので、両辺を\(\frac{1}{\sqrt{2}}\)倍すれば
\(V_e = \frac{1}{\omega C}I_e\)
あれ?これどっかで見たことある?オームの法則?
 AI
AI
まさにその通りですね。
\(R =\frac{1}{\omega C}\)とすれば
\(V_e = RI_e\)
完全にオームの法則ですよね。
つまり、交流→直流とみなしたとき、コンデンサーは抵抗と同じ役割を果たし、その大きさが
\(R = \frac{1}{\omega C}\)
となります。(これは、容量リアクタンスって言います)
やってることはコイルと同じですね。
導出できると一番いい
いかがでしたか?
こういう導出や意味づけというのは教科書や問題集ではあまり説明されていないことが多いです。そうするとただの暗記になってしまいます。
物理は暗記ではありません。この後に自分で1から状況を設定して式を導出してみる。あるいは自分自身に説明してみるといいアウトプットになりますので、ぜひやってみてください。
コイルの電流は電圧より位相が\(\frac{\pi}{2}\)だけ進む
「交流→直流」とみなすとコンデンサーは大きさ\(\frac{1}{\omega C}\)の抵抗となる









