J.J.トムソンとミリカンの実験とは?歴史の背景と流れを読み解く
どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
原子分野の最初にやるのがJ.Jトムソンの実験とミリカン実験です。
これらの実験が入試に出ても全く怖くありません。
電磁気と力学の知識で解くことができるのと、聞かれることが完全に決まっているからです。
「実験で何が求められるのか」と「実験の流れ」を知っていれば楽勝です!
この記事ではJ.J.トムソンの実験とミリカン実験の時代背景と実験の流れを分かりやすく教えます。
ここで書いてあることを覚えるつもりで理解すれば、入試で問われても満点をとれますので最後まで読んでください。
・J.Jトムソンの実験の流れが分かる
・トムソンの実験の流れが分かる
目次
J.Jトムソンとミリカンの実験の目的

J.Jトムソンとミリカンは電子について研究をしていました。
当時、電子の存在には気づいていたのですが、電子の質量と電気量は分かっていなかったのです。
それらを暴いてやろうと考えたのがこの2人です。
J.Jトムソンは電子の質量\(m\)と電気量\(e\)の比、\(\frac{e}{m}\)を求めることに成功し、ミリカンは実際に\(e\)と\(m\)の値を導きだしました。
彼らは電子の運動を考えることで求めることができたのです。
この時代背景をまずは理解しておいてください。
J.Jトムソンの実験
では、実際に実験の内容を見ていきます。
電気量の大きさが\(e\)、質量\(m\)電子の運動を考える。長さ\(l\)の極板間には図のように一様な電場\(E\)が生じている。ただし、重力は無視してよい。
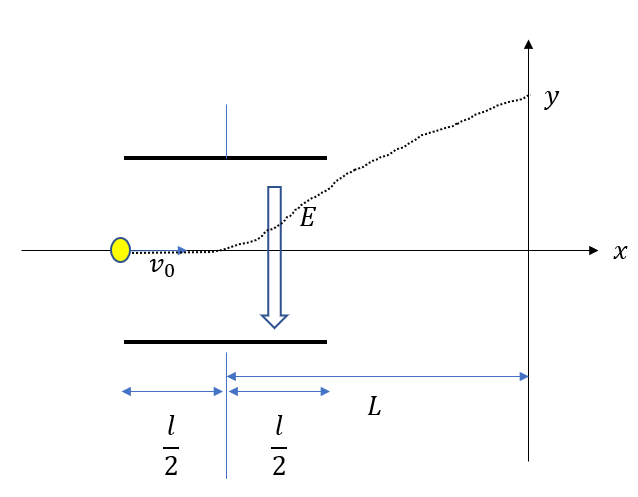
(1) 極板間に、ある向きに磁場を加えると電子は直進する。どちら向きの磁場を加えるべきか答えよ。また、磁場の大きさを\(B\)としたとき、電子の初速度\(v_0\)を求めよ。
(2) 極板間には電場のみがかかっているとして、この極板間中での電子の加速度を求めよ。
(3) 極板を通り抜けた後、電子は\(L\)だけ水平に進んだ時に位置\(y\)のところにあった。このとき\(\frac{e}{m}\)を求めよ。
これはただの電磁気と力学の問題です。実際に問題演習として解いてみましょう!
(1) 直進する=y方向の力がつり合う
まず、電場によって受ける力を考えてみます。
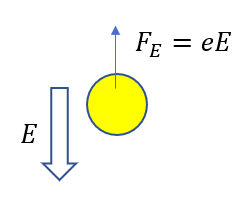
電子は負の電荷をもつので電場とは逆向き(上向き)に大きさ\(F_E = eE\)の力を受けます。
ですから、電子を直進させるには、これと同じ大きさで下向きの力を加える必要があります。
磁場を加えることでローレンツ力がはたらくので、ローレンツ力が下向きになるように磁場を調整します。
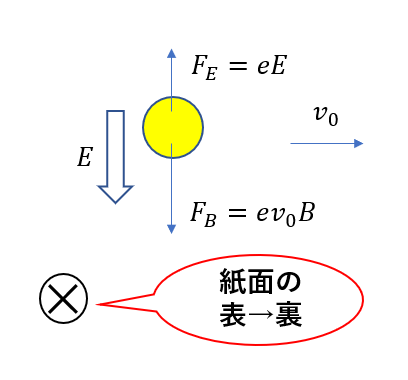
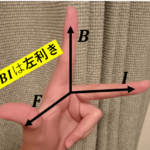
このように、紙面の表から裏向きに磁場が生じればローレンツ力は下向きに働きますね。ちなみに電子は負電荷を持つので、フレミングの左手を使う場合、中指は速度の向きと逆に合わせることに注意しましょう。
ローレンツ力についてはこちらの記事で詳しく説明しています。
こうすることで、初速度の大きさ\(v_0\)が求められます。
水平向きに動くということは垂直方向の力がつり合っているということです。
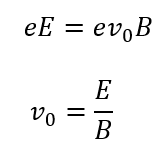
これで初速度を求めることができました。
(2) 運動方程式を立てる
これは(1)の磁場を取り除いて単純に運動方程式を立てればいいですね。

加速度が上向きなので軸も上向きに取ります。
電場による力しか働いていないので、合力は\(F_E\)です。
あとは運動方程式を適用すればOKです。特に間違えそうなポイントはないですね。
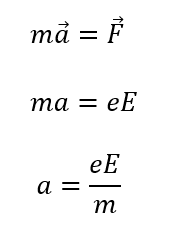
ということなので上向きに大きさ\(\frac{eE}{m}\)の加速度が生じることが分かりますね。
運動方程式の立て方についてはコチラで詳しく説明しています。
(3) 等加速度運動の公式を使おう
(3)は等加速度運動の式が使えれば解けますね。
等加速度運動についてはこちらを確認してください
- 極板間にある
- 極板間を抜けた後
極板間にあるとき
極板間を出るときの高さ\(y’\)と垂直方向の速さ\(v_y\)を求めましょう。
水平向きには加速度が生じていないので簡単に時間が求まります。
\(t = \frac{l}{v_0}\)
この時間を使って\(y’\)が求められます。
極板間にある場合は上向きに大きさ\(a =\frac{eE}{m}\)で等加速度運動していますね。
そして初速度は0です。それを踏まえて式を立てると次のように求められます。
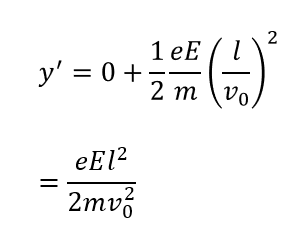
また、極板を抜ける直前の速さ\(v_y\)も求めておきましょう。
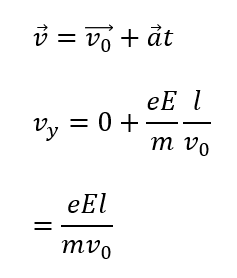
極板間を抜けた後
これも先ほどと同じように求めてみましょう。
水平方向は変わらず速さ\(v_0\)で等速運動しているので時間が簡単に求まります。
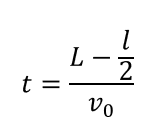
\(y\)方向に関しては極板を通過しているので加速度は生じていません。なので極板を通過したとの距離も簡単に求まります。
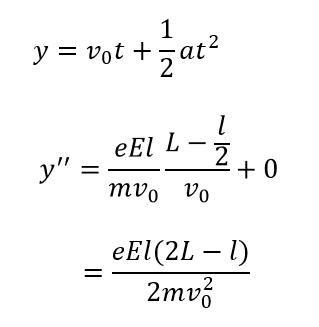
そして\(y=y’+y”\)となるので、これを計算すると\(\frac{e}{m}\)を求めることができます。
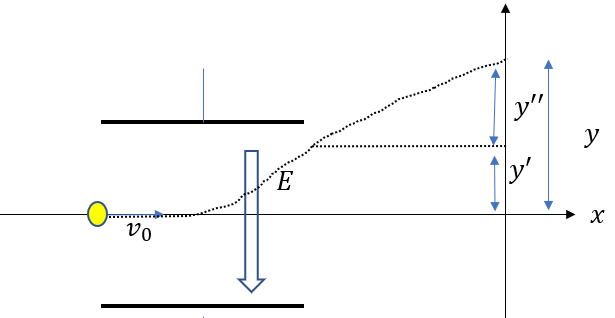
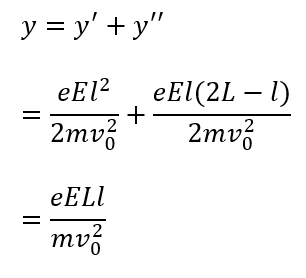

この\(\frac{e}{m}\)を比電荷と呼び、\(\frac{e}{m}=1.76\times 10^{11}\)という値になります。(この値は覚えなくていいです)
この実験の流れを理解しておいてくださいね。
ミリカンの実験
J.J.トムソンの実験では比電荷はわかりました。しかし、電子の電気量は質量が決まったわけではありません。
ミリカンはその電気量と質量を測定することに成功しました。その実験を見てみます。
ミリカンは正に帯電させた霧状の油滴を使って油滴の電荷を求めた。これについて次の問いに答えよ。ただし、油滴の電荷量を\(q\)、質量を\(M\)とする。また、速度が一定の時の空気抵抗力の大きさを\(kv\), 重力加速度の大きさを\(g\)とし、空気抵抗力と重力も考慮すること。
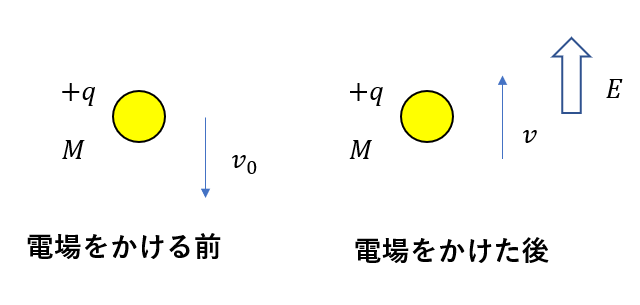
(1) 電場をかけていない状態では下向きに速さ\(v_0\)で落下した。この時の力のつり合い式を立てよ。
(2) 電場を上向きにかけると、油滴は上向きに速さ\(v\)で上昇した。この時の力のつり合い式を立てよ。また\(q\)を求めよ。
空気抵抗の向きに注目
(1)と(2)では空気抵抗の向きさえ気をつければめちゃめちゃ簡単な問題です。
(1)では下向きに落下するので空気抵抗は上向きになります。

図を見れば力のつり合いは一発ですね。上向きを正に取って
\(kv_0 – Mg = 0\)
となります。
(2) では上昇するので、空気抵抗は下向きに働きます。

上向きを正にして
\(qE – kv – Mg = 0\)
先ほどの式も使って\(q\)を求めると・・・
\(q = \frac{k(v + v_0)}{E}\)
問題としてはこれでおしまいです。
がもう少しこれについて見ていきます。
右辺はすべて求められる式なので、これにより\(q\)が導けます。
そして、ミリカンは実験の際にこのように考えていました。
電気量の元ととなる”電気素量”ってものがあるんだろう・・・仮にその電気素量を\(e\)としたら、どんな電気量も\(e\)の何倍かになっているだろう。。。
つまり、この油滴実験で得られた\(q\)の値が\(e\)の倍数であるだろうと考えたのです。
\(q\)には油滴の付き具合でばらつきがあったわけですが、どれも\(1.60×10^(-19)\)の倍数なっていることを発見したのです。
そしてこの、\(e = 1.60×10^(-19)\)が電気素量といい、マイナスをつけたものがまさに電子の電気量という結論に至りました。
これとさっきに比電荷から、電子の質量も導けます。
このような背景もしっかり理解しておいてください。
まとめ:実験の背景と流れを学べ

いかがでしかた?
ポイントは各実験のゴールと流れを把握することです。
原子分野は背景があっての問題が多いので背景をつかんでおくことで入試に出た場合も解きやすくなります。
ではしっかり復習しておきましょう!
J.Jトムソンの実験
電子の運動から比電荷\(\frac{e}{m}\)を導いた
ミリカンの実験
油滴実験により電気素量\(e\)と電子の質量\(m\)を導いた