光子のエネルギーと光電効果
さてさて、原子分野です。
今回のテーマは光電効果です
まあ、基本的には今まで学んできたことを使えばできるんだ。
でも、原子分野っていう新しい分野に入っているので、新しく覚えないといけないこともある。今回は新しく学ぶことがあるんで、そこはしっかり押さえていこうね。
今回はエネルギーが重要なので復習しておいてね。
光子のエネルギー
まずは、光子のエネルギーっていうのを学ぼう。
光ってのは粒子性(粒子としての特徴)と波動性(波としての特徴)の二つがある。そのうち、粒子性を見たときにのエネルギーを光子のエネルギーっていうんだ。
光子っていうのはその光を構成している粒子のことね。
んで、振動数\(\nu\)の光のエネルギーは、プランク定数を\(h\)とすると・・・
\(E = h\nu\)
表せる。
んで、この光の波長を\(\lambda\)、光速\(c\)とすれば、波の基本式\(v = f\lambda\)から
\(\nu = \frac{c}{\lambda}\)となるから
\(E = \frac{hc}{\lambda}\)
と表せる。
また、光を粒子の流れとすれば、当然、運動量を持っているはずだ。
その運動量は次のように表せる。
\(p = \frac{E}{c}\)
Eはさっきの光子のエネルギーを代入すると
\(p = \frac{h}{\lambda}\)
これがよく使われるから、覚えておこう!!
光電効果
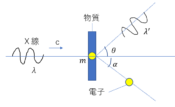
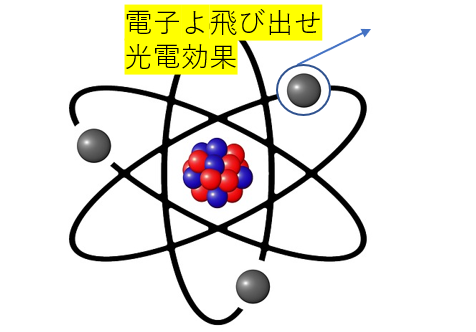
では、今回の本題。光電効果に入ろう。
金属表面に光を当てると電子が飛び出る現象を光電効果っていうよ。
光を粒子と見れば、この粒子はエネルギーを持っているから、電子に衝突することで、電子にエネルギーを与えることができる。電子は運動エネルギーを持つようになるので、電子が飛び出るってわけだ。

結局はエネルギー問題ってわけだね。
じゃあ、電子が飛び出るにはどのくらいのエネルギーを与えればいいのか?
坂道を転がる電子をモデルに考えてみよう!!
仕事関数

まず、ギリギリ坂道を上る場合を考えよう。
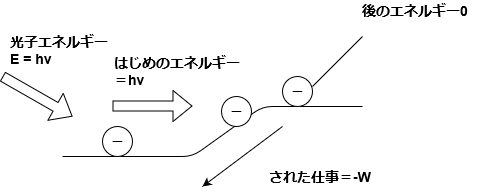
まず、光子を電子をあてると、電子は仕事されるのでエネルギーを得るんだね。
仕事をされた分だけエネルギーが増えるってことだね。
んで、坂道を上るのに必要なエネルギー(つまり、坂道からされる)仕事がWとすれば、
(初めのエネルギー)+(された仕事)=(あとのエネルギー)
から
\(h\nu + (-W) = 0\)
∴\(W = h\nu\)
このWは電子が飛び出るのに必要最低限のエネルギーだね
そのエネルギーWを仕事関数っていうんだ。
んで、その時の振動数を\(\nu_0\)(限界振動数)っていうもので強調すると
\(W = h\nu_0\)
となる。
このWが基準になってくる。
電子が飛び出ない場合は

ってことで、光子エネルギーが仕事関数より小さいってことがわかるよね。
\(h\nu < W\)
じゃあ、次に電子が余裕で飛び出る場合を考えよう。
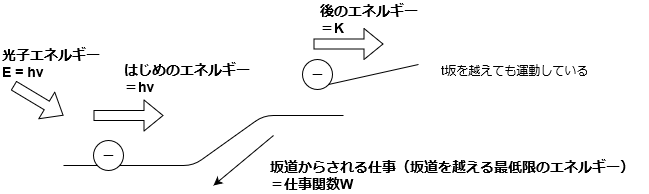
今回は、余裕で飛び出るので、坂を越えた後も運動しているんだ。つまり、運動エネルギーKをもつってことだね。
あとは
(はじめのエネルギー)+(された仕事)=(後のエネルギー)
を使えば
\(h\nu + (-W) = K\)
\(K = h\nu – W\)
ってなる。
このKは運動エネルギーなんだけど、電子の最大運動エネルギーね。
電子のエネルギーのグラフ
最後にこの\(K = h\nu – W\)をグラフで見るとどうなるかっていうのを学ぼう。
これをKと\(\nu\)の関数と見ると、一次関数だよね。
傾きが\(h\)、y切片が\(-W\)の直線になる。
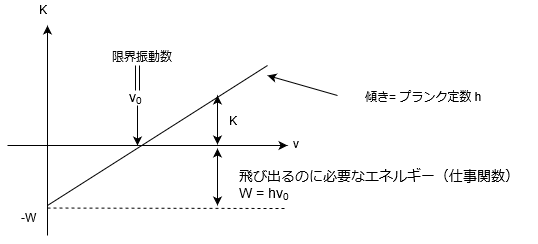
ま、グラフがさっきの坂道のイメージそっくりですよね。
-W(y切片)からスタートして\(\nu\)軸が坂道の頂上ですよね。んで、\(\nu_0\)にたどり着くまでは、坂道を上る必要があるので、これが仕事関数はWになる。
んで、余裕で飛び出るなら、飛び出た分だけ運動エネルギーKが蓄えられる。
ってことで、光電効果でした。
結局はエネルギーの問題ってことが分かったね。
次回は光電効果を解いてみよう